So erstellen sie ein binomialverteilungsdiagramm in excel

Die Binomialverteilung wird verwendet, um die Wahrscheinlichkeit zu beschreiben, in n Binomialexperimenten k Erfolge zu erzielen.

Ein Binomialexperiment ist ein Experiment mit den folgenden Eigenschaften:

• Das Experiment besteht aus n wiederholten Versuchen.
• Jeder Versuch hat nur zwei mögliche Ergebnisse.
• Die Erfolgswahrscheinlichkeit, p genannt, ist für jeden Versuch gleich.
• Jeder Test ist unabhängig.

Wenn eine Zufallsvariable X einer Binomialverteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Gold:

• n : Anzahl der Versuche
• k : Anzahl der Erfolge
• p : Erfolgswahrscheinlichkeit bei einem bestimmten Versuch
• _n C _k : die Anzahl der Möglichkeiten, in n Versuchen k Erfolge zu erzielen

Das folgende Beispiel zeigt, wie man in Excel ein Binomialverteilungsdiagramm erstellt.

Beispiel: Binomialverteilungsdiagramm in Excel

Um ein Binomialverteilungsdiagramm zu erstellen, müssen wir zunächst einen Wert für n (Anzahl der Versuche) und p (Erfolgswahrscheinlichkeit in einem bestimmten Versuch) festlegen:

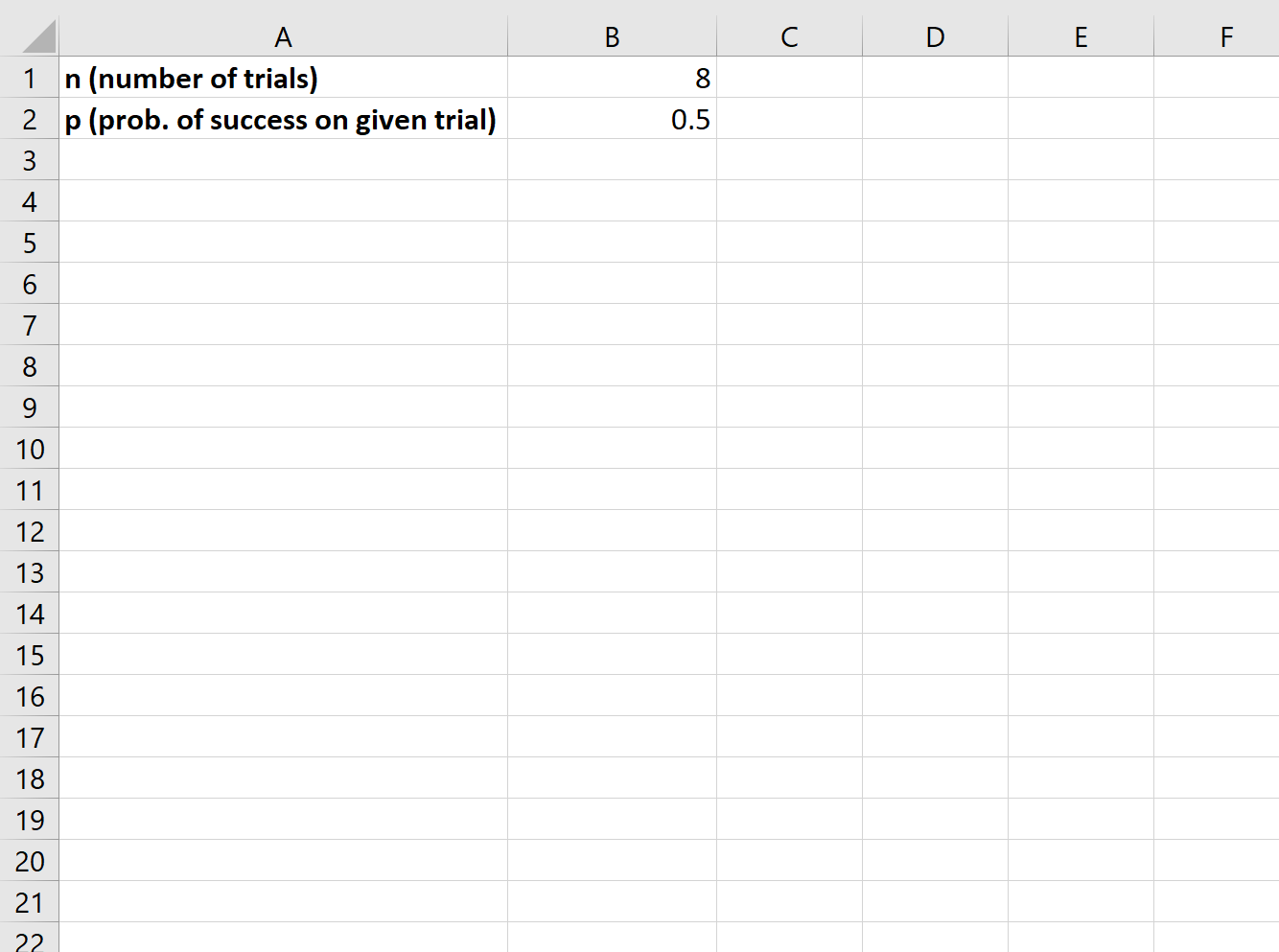
Als nächstes müssen wir für jede mögliche Anzahl von Erfolgen eine Spalte erstellen:

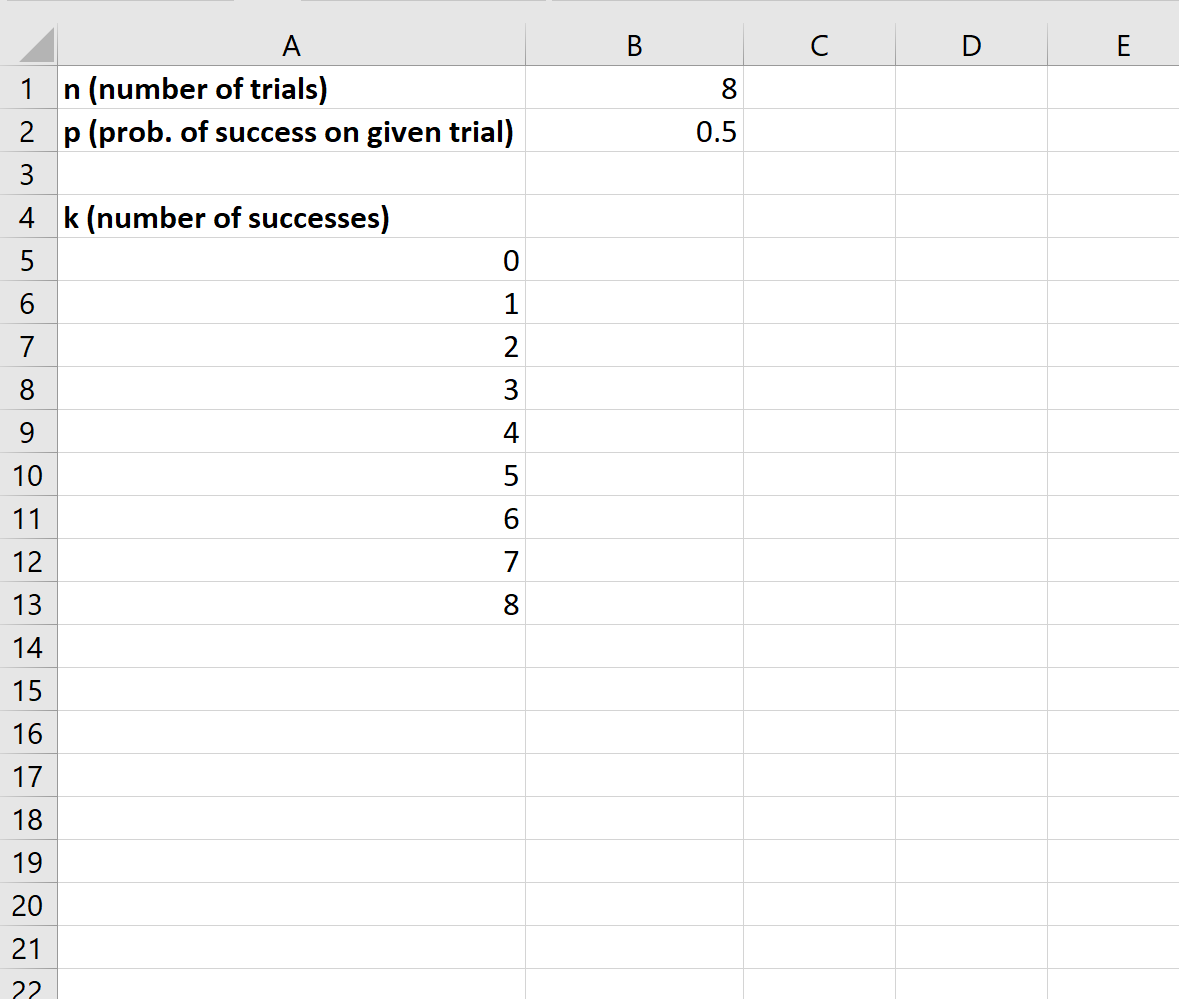
Als nächstes können wir die Funktion BINOM.DIST() verwenden, um die Binomialwahrscheinlichkeit der ersten Anzahl von Erfolgen zu berechnen:

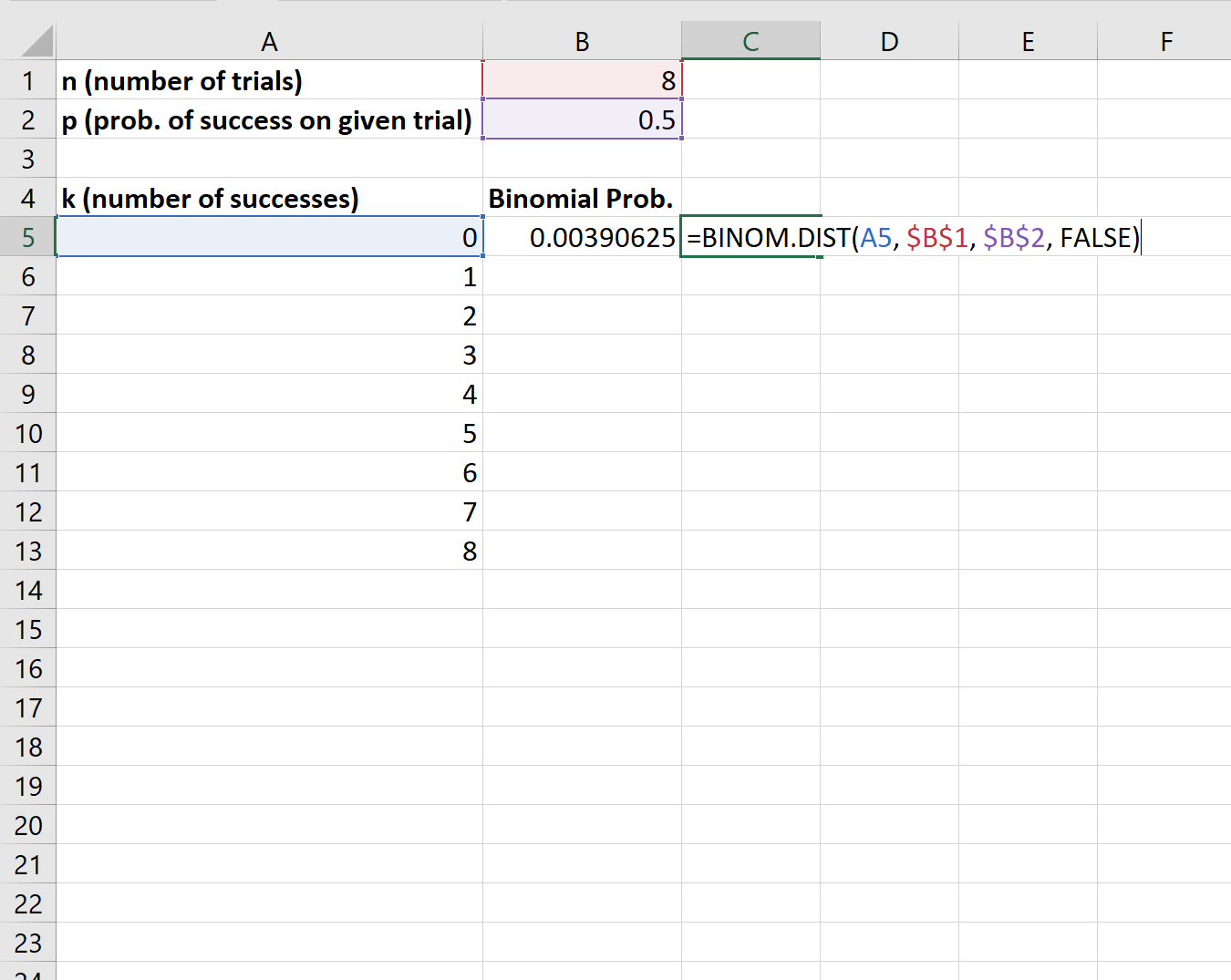
Anschließend können wir diese Formel kopieren und in die verbleibenden Zellen in Spalte B einfügen:

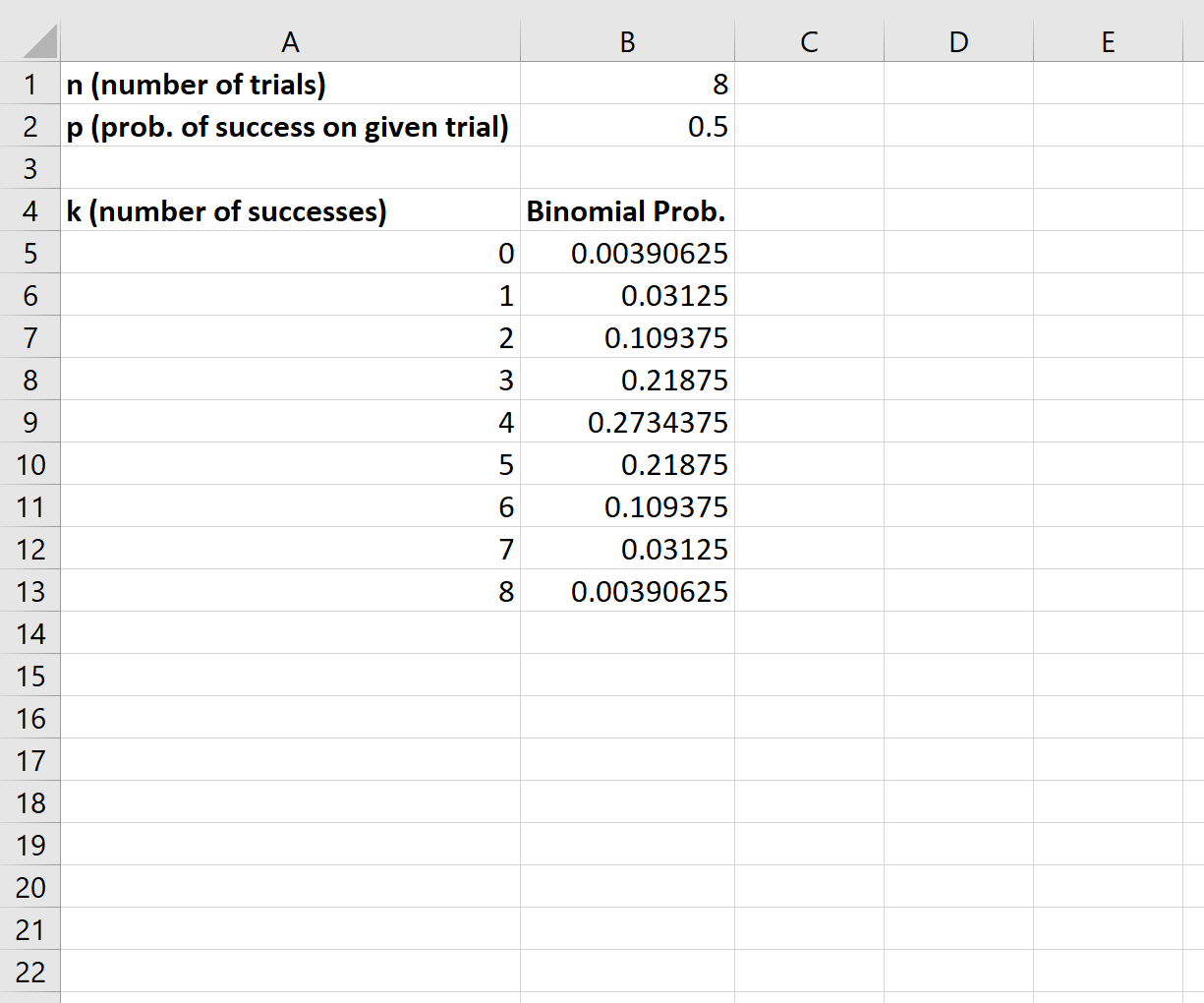
Schließlich können wir jede der Binomialwahrscheinlichkeiten hervorheben, dann im oberen Menüband auf die Registerkarte „Einfügen “ klicken und dann in der Gruppe „Diagramme “ auf das Symbol „Säulen- oder Balkendiagramm einfügen“ klicken:

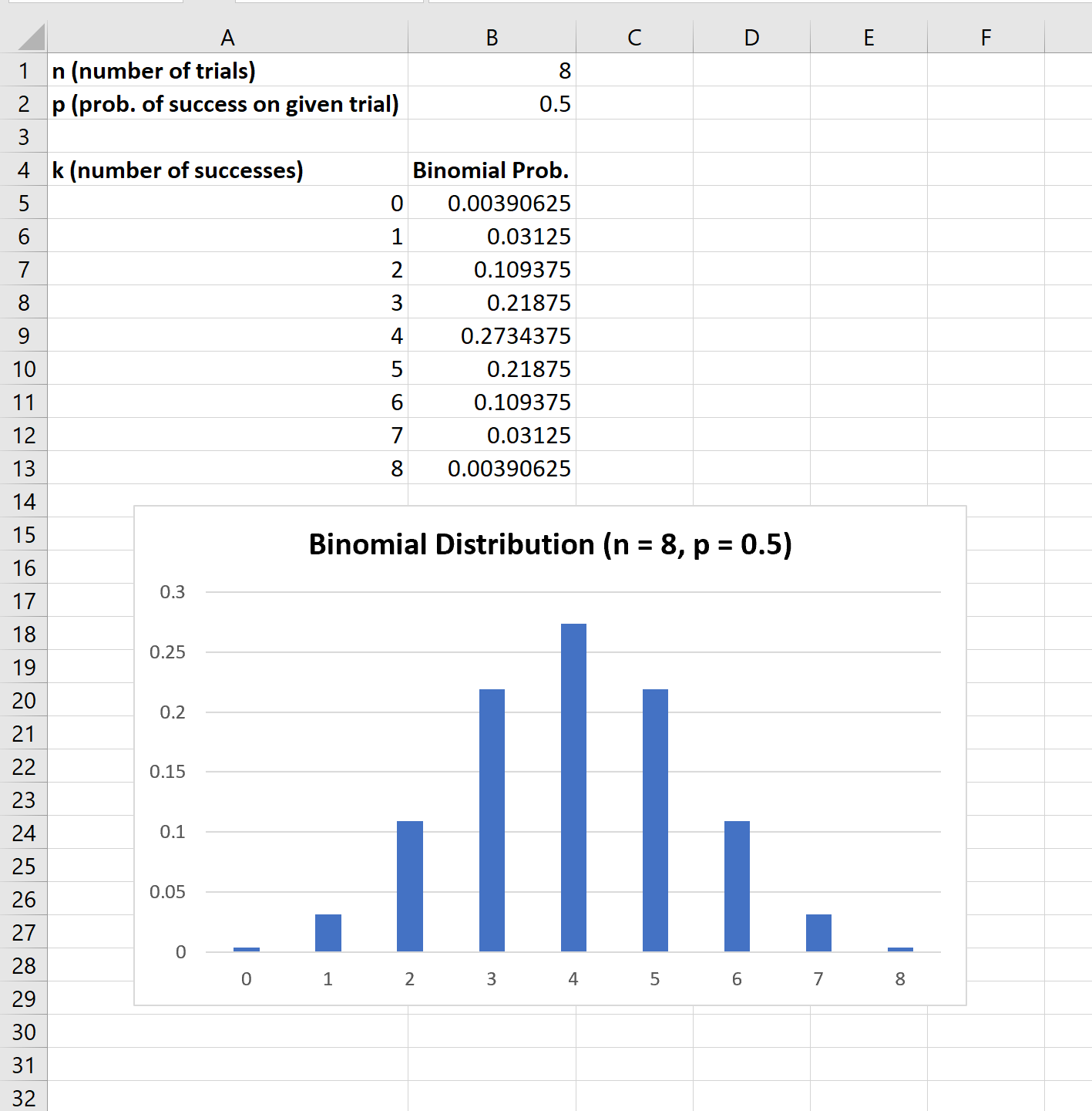
Die x-Achse des Diagramms zeigt die Anzahl der Erfolge in 8 Versuchen und die y-Achse zeigt die entsprechende Wahrscheinlichkeit dieser Anzahl an Erfolgen.

Beachten Sie, dass sich das Diagramm automatisch ändert, um die neuen Wahrscheinlichkeiten widerzuspiegeln, wenn Sie den Wert von n oder p ändern.

Zusätzliche Ressourcen

Eine Einführung in die Binomialverteilung
Die Form einer Binomialverteilung verstehen
5 konkrete Beispiele der Binomialverteilung