Excel: so verwenden sie linest zur durchführung einer multiplen linearen regression

Sie können die LINEST- Funktion in Excel verwenden, um ein multiples lineares Regressionsmodell an einen Datensatz anzupassen.

Diese Funktion verwendet die folgende grundlegende Syntax:

 = LINEST ( known_y's, [known_x's], [const], [stats] )

Gold:

• bekannte_y’s : ein Array bekannter y-Werte
• known_x’s : ein Array bekannter x-Werte
• const : Optionales Argument. Wenn TRUE, wird Konstante b normal verarbeitet. Bei FALSE wird die Konstante b auf 1 gesetzt.
• Statistiken : Optionales Argument. Bei TRUE werden zusätzliche Regressionsstatistiken zurückgegeben. Bei FALSE werden keine zusätzlichen Regressionsstatistiken zurückgegeben.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie diese Funktion in der Praxis nutzen.

Schritt 1: Geben Sie die Daten ein

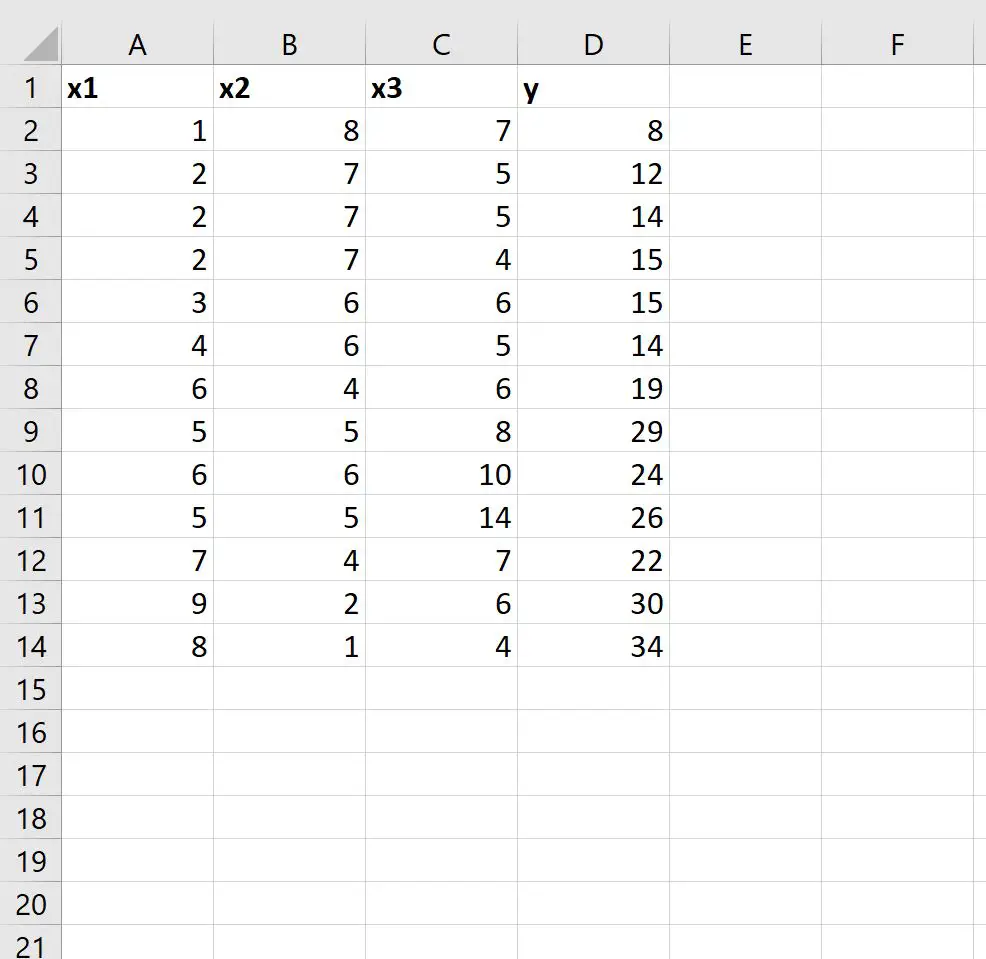
Geben wir zunächst den folgenden Datensatz in Excel ein:

Schritt 2: Verwenden Sie LINEST, um ein multiples lineares Regressionsmodell anzupassen

Angenommen, wir möchten ein multiples lineares Regressionsmodell anpassen, indem wir x1 , x2 und x3 als Prädiktorvariablen und y als Antwortvariable verwenden.

Dazu können wir die folgende Formel in eine beliebige Zelle eingeben, um sie an dieses multiple lineare Regressionsmodell anzupassen

 =LINEST( D2:D14 , A2:C14 )

Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:

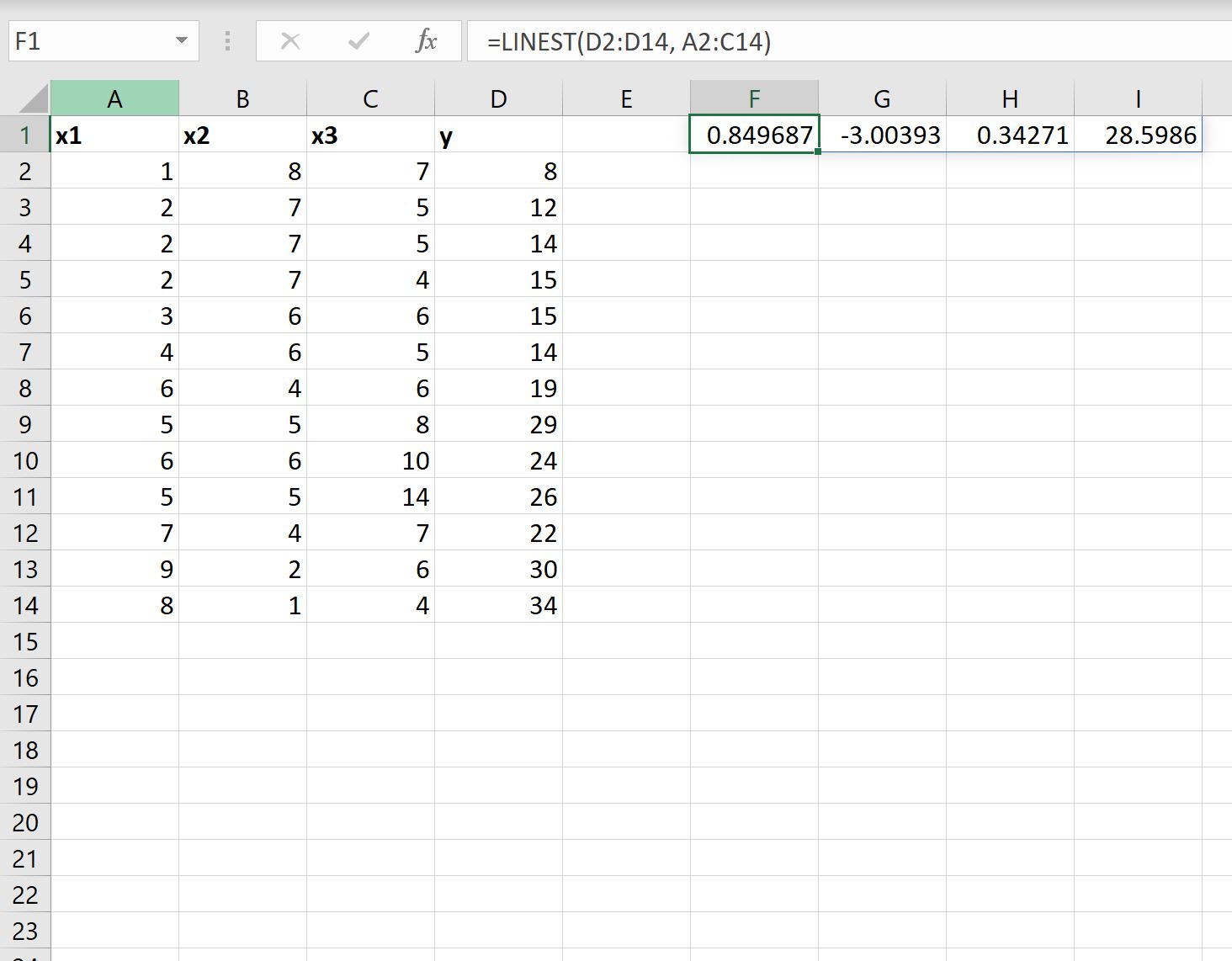
So interpretieren Sie das Ergebnis:

• Der Koeffizient des Achsenabschnitts beträgt 28,5986 .
• Der Koeffizient für x1 beträgt 0,34271 .
• Der Koeffizient für x2 beträgt -3,00393 .
• Der Koeffizient für x3 beträgt 0,849687 .

Mit diesen Koeffizienten können wir die angepasste Regressionsgleichung wie folgt schreiben:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Schritt 3 (optional): Sehen Sie sich zusätzliche Regressionsstatistiken an

Wir können auch den Wert des Stats- Arguments in der LINEST- Funktion auf TRUE setzen, um zusätzliche Regressionsstatistiken für die angepasste Regressionsgleichung anzuzeigen:

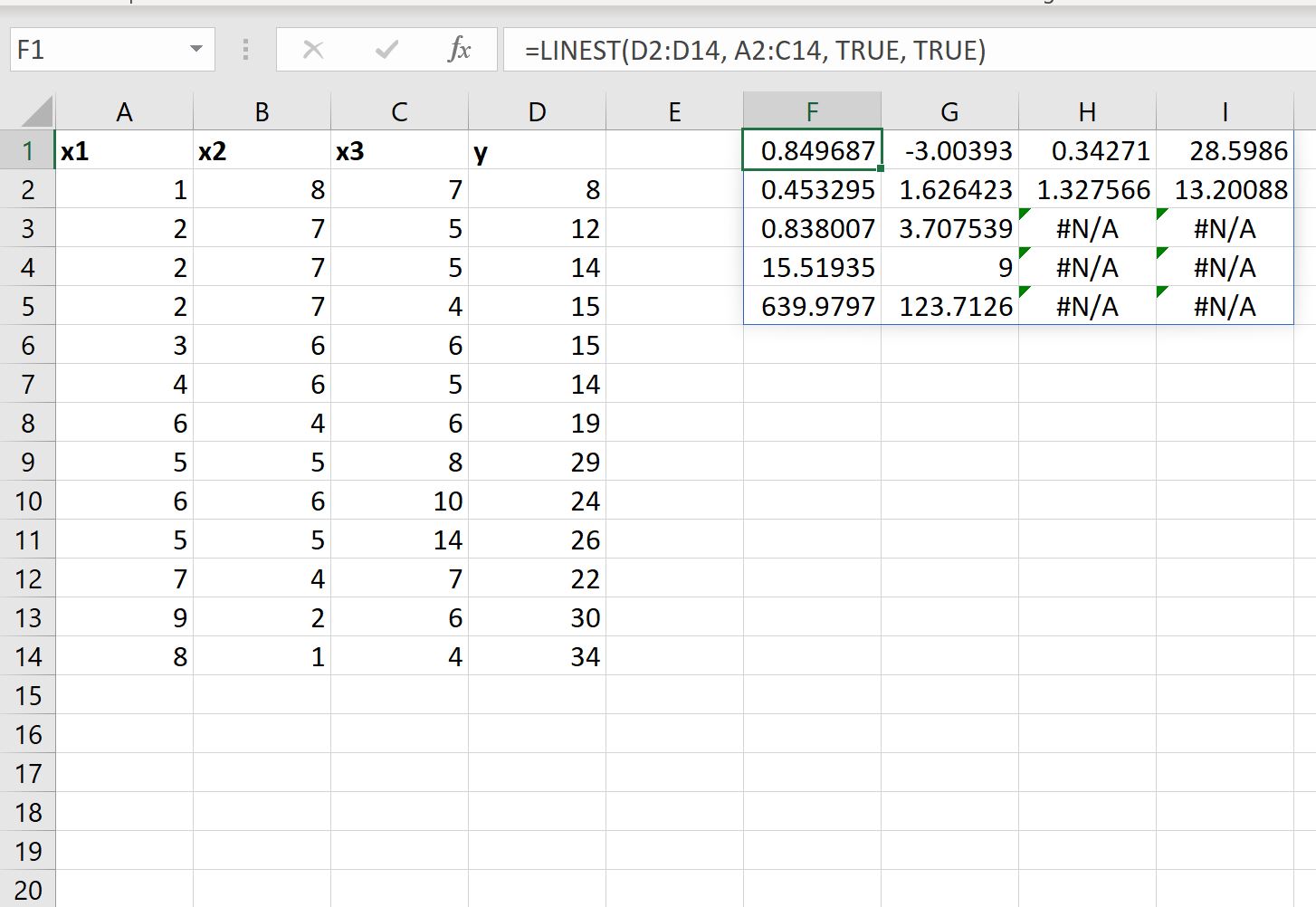
Die angepasste Regressionsgleichung ist immer noch dieselbe:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

So interpretieren Sie die anderen Werte des Ergebnisses:

• Der Standardfehler für x3 beträgt 0,453295 .
• Der Standardfehler für x2 beträgt 1,626423 .
• Der Standardfehler für x1 beträgt 1,327566 .
• Der Standardfehler für den Abschnitt beträgt 13,20088 .
• Der R ² des Modells beträgt .838007 .
• Der verbleibende Standardfehler für y beträgt 3,707539 .
• Die Gesamt-F-Statistik beträgt 15,51925 .
• Die Freiheitsgrade betragen 9 .
• Die Regressionsquadratsumme beträgt 639,9797 .
• Die verbleibende Quadratsumme beträgt 123,7126 .

Im Allgemeinen ist das Maß von größtem Interesse in diesen zusätzlichen Statistiken der R ² -Wert, der den Anteil der Varianz in der Antwortvariablen darstellt, der durch die Prädiktorvariable erklärt werden kann.

Der Wert von R ² kann zwischen 0 und 1 variieren.

Da das R ² dieses speziellen Modells 0,838 beträgt, zeigt uns dies, dass die Prädiktorvariablen den Wert der Antwortvariablen y gut vorhersagen können.

Verwandt: Was ist ein guter R-Quadrat-Wert?

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge in Excel ausführen:

So verwenden Sie die LOGEST-Funktion in Excel
So führen Sie eine nichtlineare Regression in Excel durch
So führen Sie eine kubische Regression in Excel durch