Excel: erstellen sie einen statistischen vergleich zweier datensätze

Häufig möchten Sie möglicherweise einen statistischen Vergleich zweier Datensätze in Excel durchführen, um zu verstehen, wie sich die Werteverteilung in den einzelnen Datensätzen unterscheidet.

Es gibt zwei gängige Methoden zur Durchführung eines statistischen Vergleichs:

Methode 1: Berechnen Sie die fünfstellige Zusammenfassung jedes Datensatzes

Wir können die fünfstellige Zusammenfassung jedes Datensatzes berechnen, die aus den folgenden Werten besteht:

• Der Mindestwert
• Das erste Quartil (25. Perzentil)
• Der Median (50. Perzentil)
• Das dritte Quartil (75. Perzentil)
• Das Maximum

Durch die Berechnung dieser fünf Werte können wir ein gutes Verständnis der Werteverteilung in jedem Datensatz erlangen.

Methode 2: Berechnen Sie den Mittelwert und die Standardabweichung

Eine einfachere Möglichkeit, einen statistischen Vergleich zweier Datensätze durchzuführen, besteht darin, den Mittelwert und die Standardabweichung jedes Datensatzes zu berechnen.

Dies hilft uns ungefähr zu verstehen, wo der „zentrale“ Wert liegt und wie die Werteverteilung in jedem Datensatz ist.

Das folgende Beispiel zeigt, wie jede dieser Methoden in der Praxis angewendet wird.

Beispiel: Führen Sie einen statistischen Vergleich zweier Datensätze in Excel durch

Angenommen, wir haben in Excel zwei Datensätze, die die Ergebnisse von Schülern aus zwei verschiedenen Klassen zeigen, die bei einer bestimmten Prüfung erzielt wurden:

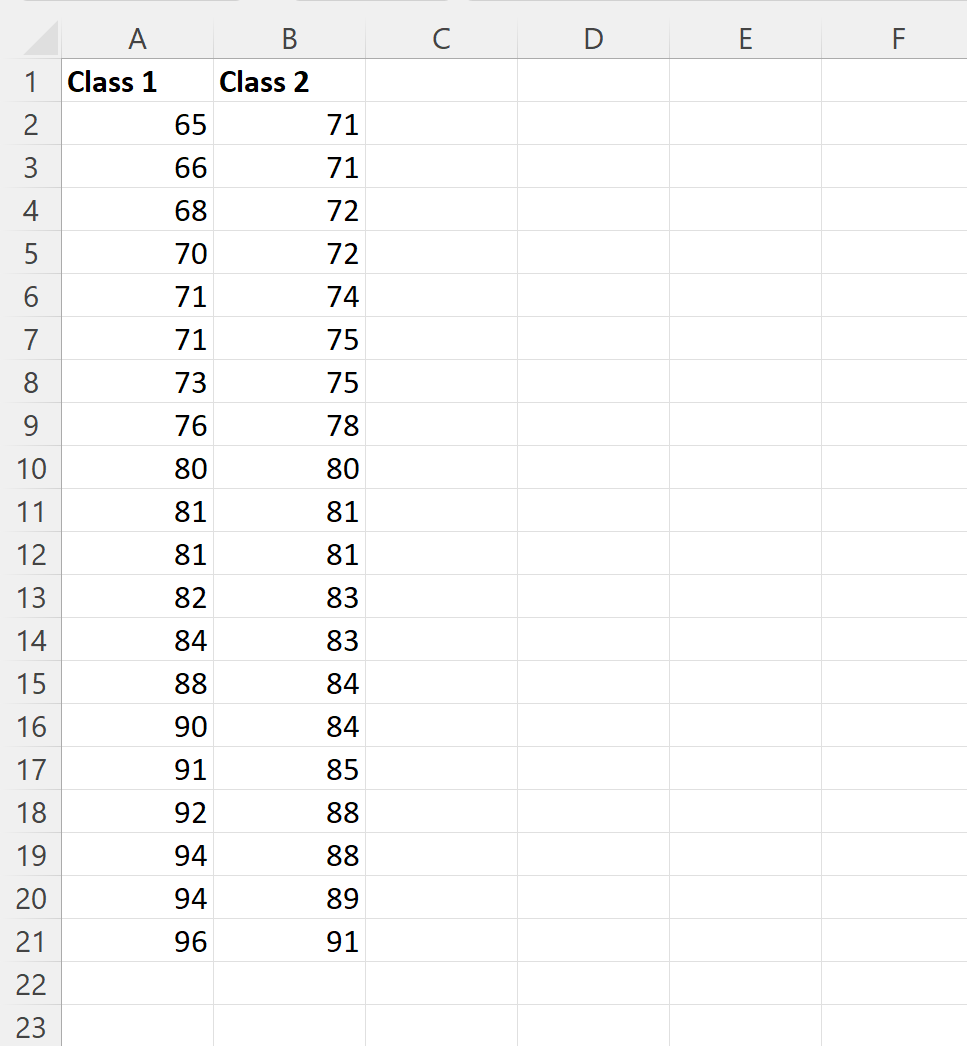
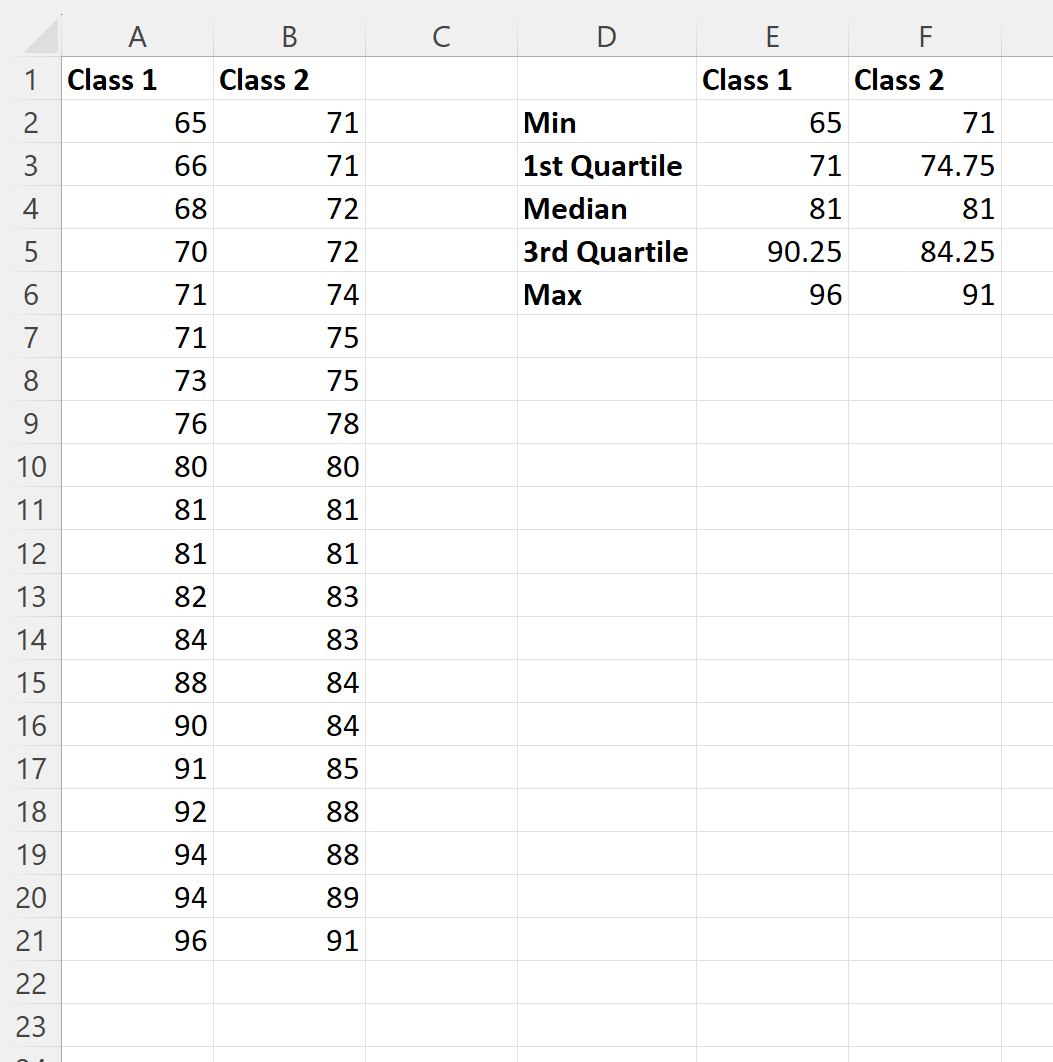
Wir können die folgenden Formeln in die Zellen der Spalte E eingeben, um die fünfstellige Zusammenfassung der Prüfungsergebnisse für Klasse 1 zu berechnen:

• E2 : =MIN(A2:A21)
• E3 : =QUARTIL(A2:A21, 1)
• E4 : =MEDIAN(A2:A21)
• E5 : =QUARTIL(A2:A21, 3)
• E6 : =MAX(A2:A21

Wir können dann auf diese Formeln klicken und sie nach rechts ziehen, um die gleichen Werte für Klasse 2 zu berechnen:

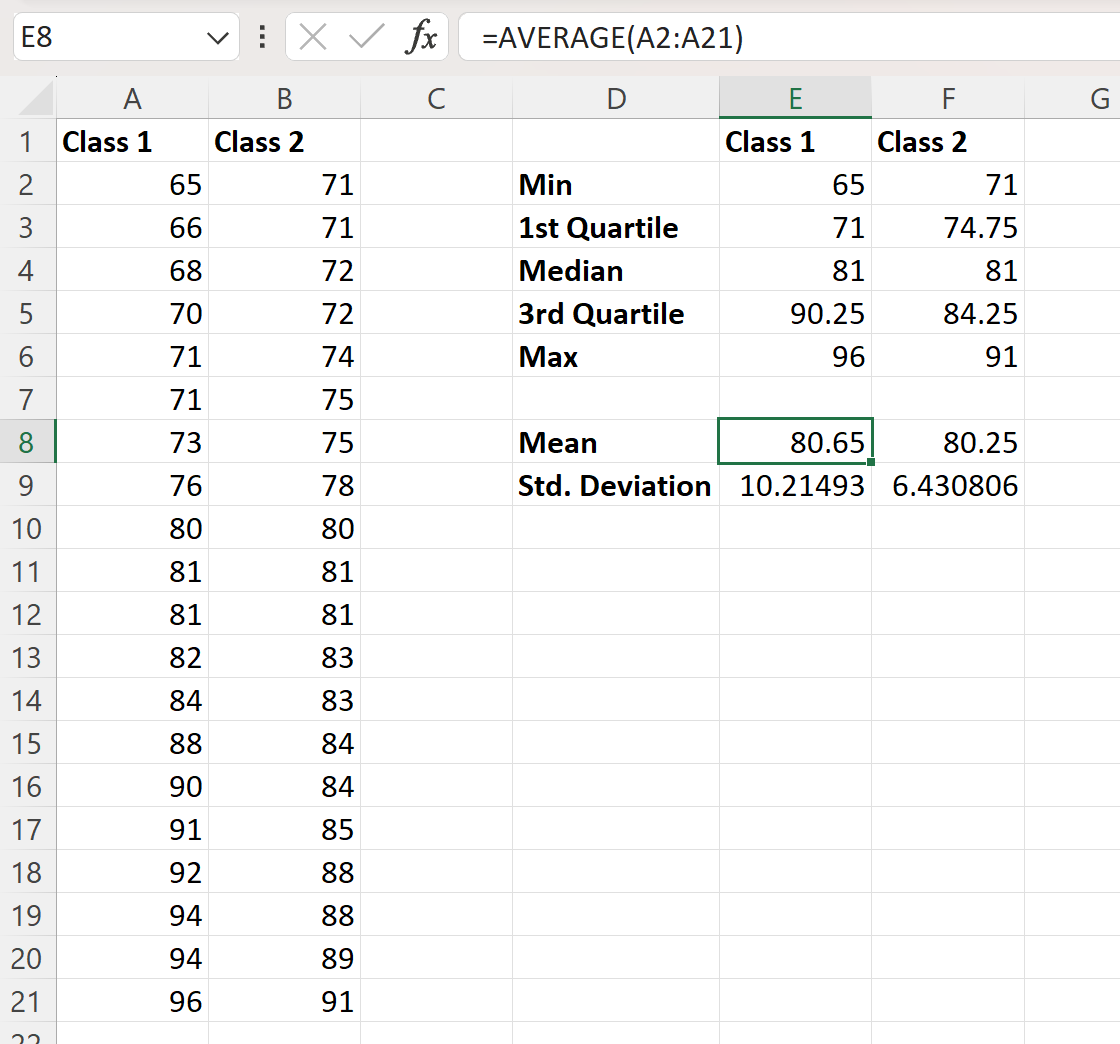
Anschließend können wir in die Zellen der Spalte E die folgenden Formeln eingeben, um den Mittelwert und die Standardabweichung der Prüfungsergebnisse für Klasse 1 zu berechnen:

• E8 : =DURCHSCHNITT(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

Wir können dann auf diese Formeln klicken und sie nach rechts ziehen, um die gleichen Werte für Klasse 2 zu berechnen:

Aus diesem statistischen Vergleich der beiden Datensätze können wir folgende Schlussfolgerungen ziehen:

Schlussfolgerung 1: Beide Datensätze haben einen ähnlichen „Kernwert“.

Beide Datensätze haben eine mittlere Prüfungspunktzahl von 81. Die Durchschnittswerte unterscheiden sich nur geringfügig: Die erste Klasse hat eine durchschnittliche Prüfungspunktzahl von 80,65, während die zweite Klasse eine durchschnittliche Prüfungspunktzahl von 80,65 hat, während die zweite Klasse eine durchschnittliche Prüfungspunktzahl von hat 80,65 ‚ Rezension von 80,25.

Dies zeigt uns, dass die „Kern“- oder „typische“ Prüfungspunktzahl zwischen den beiden Klassen ähnlich ist.

Schlussfolgerung 2: Der erste Datensatz weist eine viel größere „Streuung“ der Werte auf.

Mehrere Indikatoren deuten darauf hin, dass die Ergebnisse der Prüfungen der ersten Klasse deutlich unterschiedlicher ausfallen als die der zweiten Klasse.

Beispielsweise ist der Umfang der Klasse 1 viel höher:

• Bereich der Klasse 1: 96 – 65 = 31
• Bereich der Klasse 2: 91 – 71 = 20

Auch der Interquartilbereich der Klasse 1 ist deutlich höher:

• Interquartilbereich der Klasse 1: 90,25 – 71 = 19,25
• Interquartilbereich der Klasse 2: 84,25 – 74,75 = 9,5

Auch die Standardabweichung der Klasse 1 ist deutlich höher:

• Standardabweichung der Klasse 1: 10,21
• Standardabweichung der Klasse 2: 6,43

Jede dieser Messungen zeigt uns, dass der Unterschied in den Prüfungsergebnissen für Schüler der Klasse 1 viel größer ist als für Schüler der Klasse 2.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge in Excel ausführen:

So erstellen Sie eine Übersichtstabelle in Excel
So berechnen Sie den Median nach Gruppen in Excel
So berechnen Sie die Standardabweichung und ignorieren Null in Excel