So führen sie einen t-test mit ungleichen varianzen in excel durch

Ein T-Test mit zwei Stichproben wird verwendet, um zu bestimmen, ob die Mittelwerte zweier Grundgesamtheiten gleich sind oder nicht.

Es gibt zwei Versionen der beiden T-Test-Beispiele, die Sie verwenden können:

• t-Test mit gleichen Varianzen
• t-Test mit ungleichen Varianzen

Wir verwenden einen T-Test mit ungleichen Varianzen, wenn die Varianzen der beiden Stichproben nicht gleich sind.

Der einfachste Weg, um festzustellen, ob die Varianzen zwischen den beiden Stichproben gleich sind, ist die Verwendung der Varianz-Faustregel .

Als allgemeine Regel gilt: Wenn das Verhältnis der größten zur kleinsten Varianz kleiner als 4 ist, können wir davon ausgehen, dass die Varianzen ungefähr gleich sind.

Andernfalls, wenn das Verhältnis gleich oder größer als 4 ist, wird davon ausgegangen, dass die Varianzen nicht gleich sind.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie in Excel einen T-Test bei zwei Stichproben mit ungleichen Varianzen durchführen.

Schritt 1: Geben Sie die Daten ein

Angenommen, wir möchten feststellen, ob zwei unterschiedliche Studienmethoden zu unterschiedlichen durchschnittlichen Prüfungsergebnissen bei Studenten einer bestimmten Universität führen.

Wir wählen eine Zufallsstichprobe von 20 Studenten aus, die jede Lernmethode anwenden und ihre Prüfungsergebnisse protokollieren:

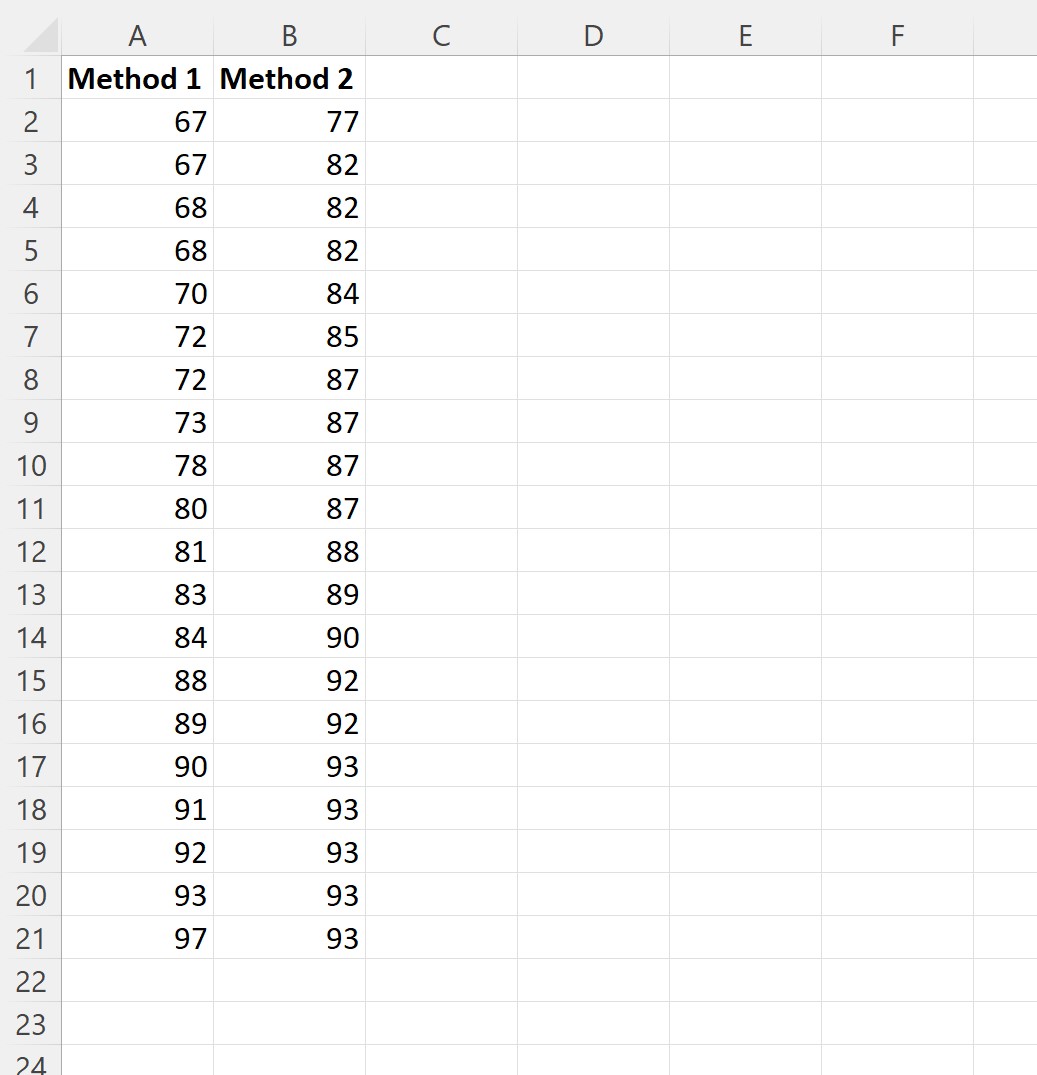
Schritt 2: Bestimmen Sie die gleiche oder ungleiche Varianz

Dann können wir das Verhältnis der Stichprobenvarianzen berechnen:

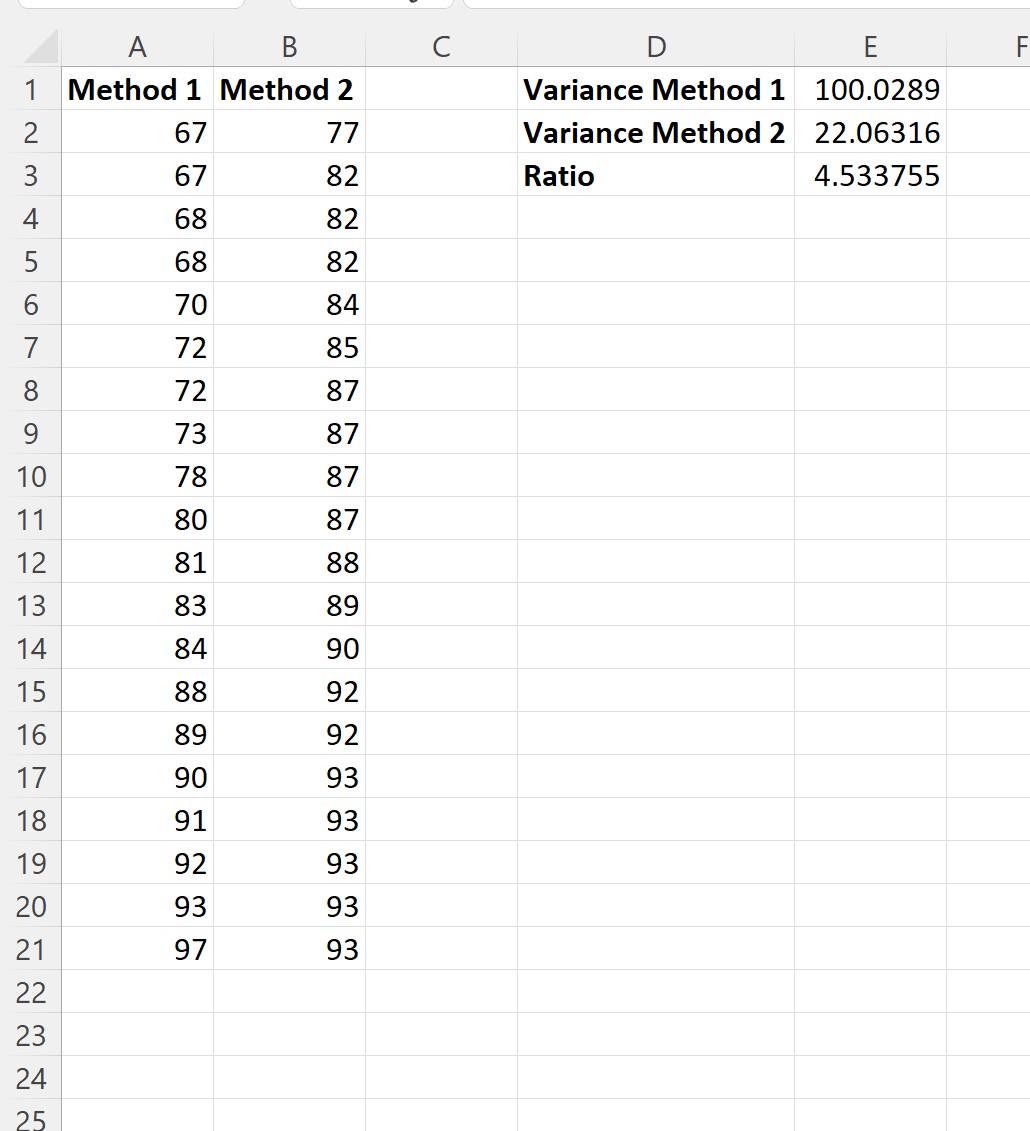
Hier sind die Formeln, die wir in jede Zelle eingegeben haben:

• Zelle E1: =VAR.S(A2:A21)
• Zelle E2: =VAR.S(B2:B21)
• Zelle E3: =E1/E2

Wir können sehen, dass das Verhältnis der größten Stichprobenvarianz zur kleinsten Stichprobenvarianz 4,533755 beträgt.

Da dieser Wert größer oder gleich 4 ist, gehen wir davon aus, dass die Varianzen zwischen den beiden Stichproben nicht gleich sind.

Schritt 3: Führen Sie einen T-Test bei zwei Stichproben mit ungleicher Varianz durch

Als Nächstes können wir einen T-Test bei zwei Stichproben mit ungleichen Varianzen durchführen, um zu bestimmen, ob die durchschnittliche Prüfungspunktzahl zwischen den beiden Stichproben gleich ist.

Klicken Sie dazu im oberen Menüband auf die Registerkarte „Daten “ und dann in der Gruppe „Analysieren“ auf die Schaltfläche „Datenanalyse“ :

Wenn Sie diese Schaltfläche nicht sehen, müssen Sie zunächst das kostenlose Data Analysis Toolpak in Excel installieren .

Klicken Sie im neuen Fenster, das erscheint, auf T-Test: Zwei Stichproben unter der Annahme ungleicher Varianzen und dann auf OK :

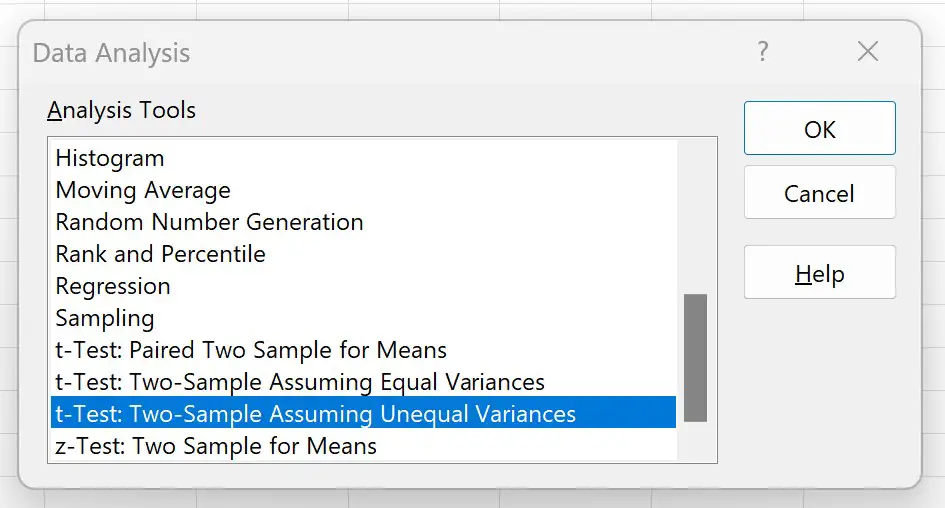
Geben Sie im neuen Fenster, das erscheint, die folgenden Informationen ein und klicken Sie dann auf OK :

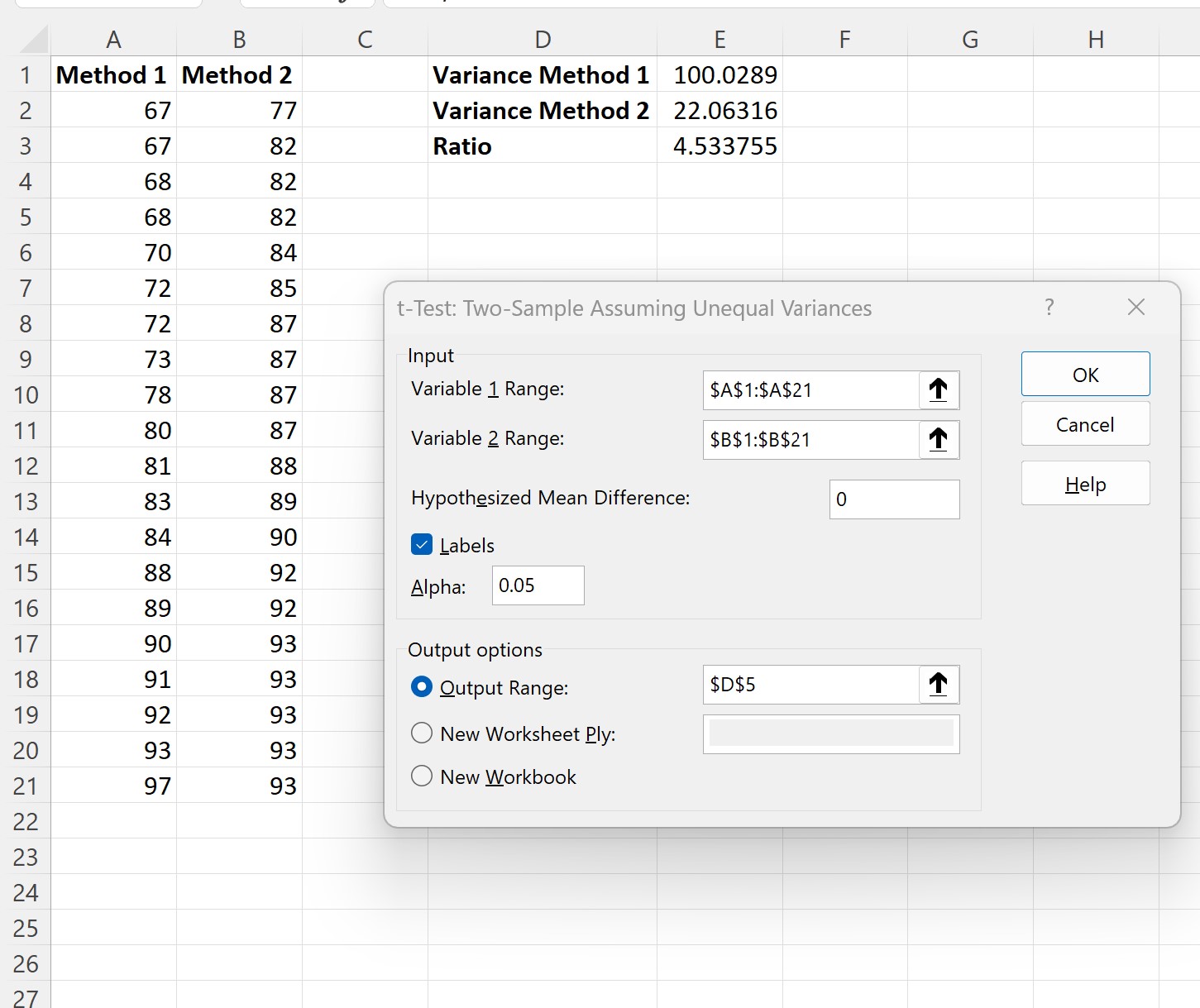
Sobald Sie auf OK klicken, werden die Ergebnisse der beiden T-Test-Beispiele angezeigt:

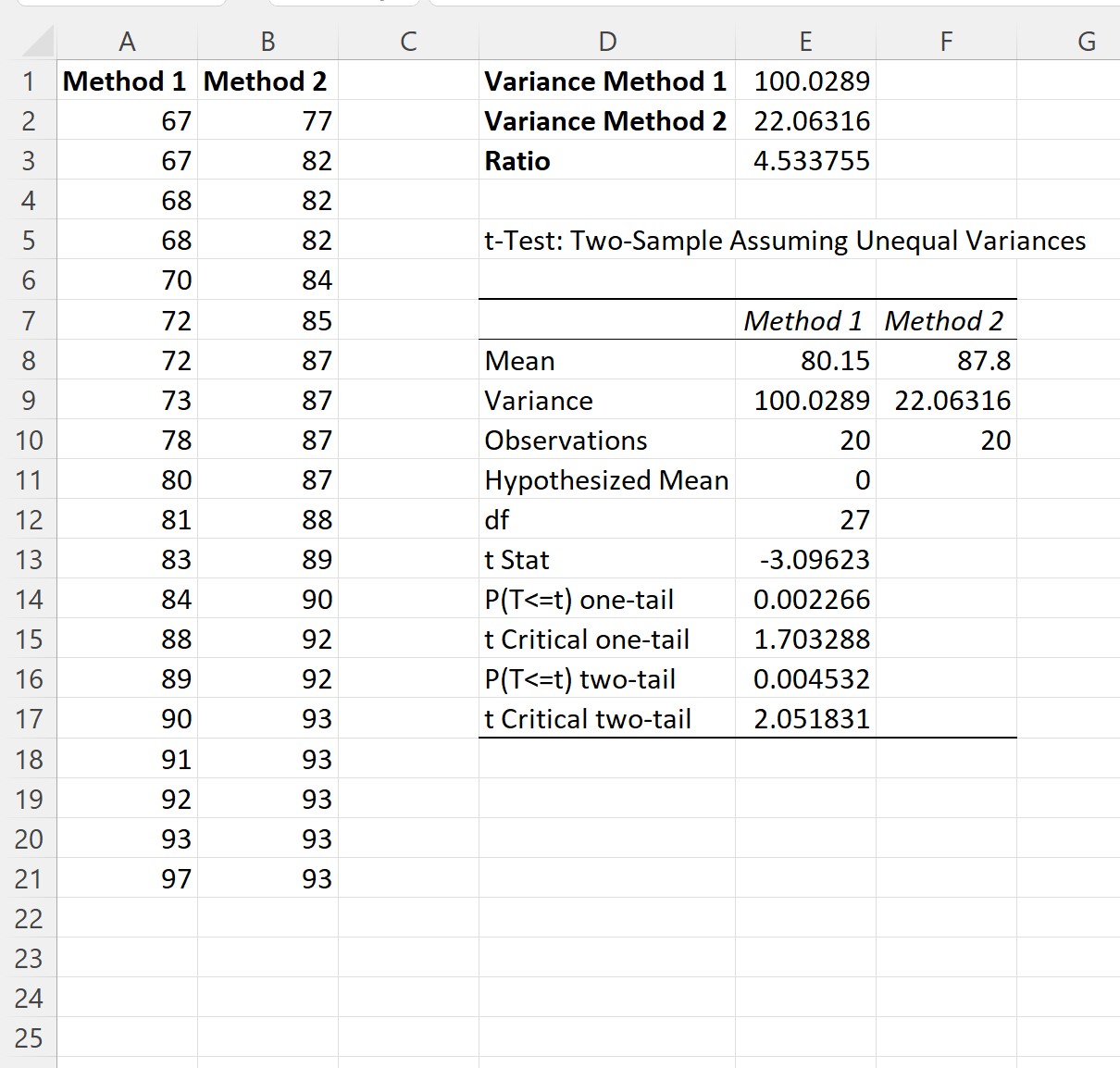
Schritt 4: Interpretieren Sie die Ergebnisse

Aus dem Ergebnis können wir sehen:

• Die durchschnittliche Prüfungspunktzahl für Methode 1 betrug 80,15 .
• Die durchschnittliche Prüfungspunktzahl für Methode 2 betrug 87,8 .
• Die T-Test-Statistik war -3,09623 .
• Der entsprechende zweiseitige p-Wert betrug 0,004532 .

Da dieser p-Wert kleiner als 0,05 ist, können wir daraus schließen, dass es einen statistisch signifikanten Unterschied in den durchschnittlichen Prüfungsergebnissen zwischen den beiden Untersuchungsmethoden gibt.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erklärt, wie Sie andere häufige Aufgaben in Excel ausführen:

So führen Sie einen T-Test bei einer Stichprobe in Excel durch
So führen Sie einen T-Test für gepaarte Stichproben in Excel durch
So führen Sie Z-Tests mit einer Stichprobe und zwei Stichproben in Excel durch