Exponentialverteilung
In diesem Artikel wird erklärt, was die Exponentialverteilung in der Statistik ist und wofür sie verwendet wird. Ebenso finden Sie die Eigenschaften der Exponentialverteilung sowie ihre Formeln, ihren Graphen und eine gelöste Übung. Darüber hinaus können Sie jede beliebige Wahrscheinlichkeit mit einem Online-Exponentialverteilungsrechner berechnen.
Was ist Exponentialverteilung?
Die Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die zur Modellierung der Wartezeit für das Auftreten eines Zufallsphänomens verwendet wird.
Genauer gesagt ermöglicht uns die Exponentialverteilung, die Wartezeit zwischen zwei Ereignissen zu beschreiben, die einer Poisson-Verteilung folgt. Daher ist die Exponentialverteilung eng mit der Poisson-Verteilung verwandt.
Die Exponentialverteilung hat einen charakteristischen Parameter, der durch den griechischen Buchstaben λ dargestellt wird und angibt, wie oft das untersuchte Ereignis in einem bestimmten Zeitraum voraussichtlich auftritt.
![]()
Ebenso wird die Exponentialverteilung auch zur Modellierung der Zeit bis zum Auftreten eines Ausfalls verwendet. Die Exponentialverteilung hat daher mehrere Anwendungen in der Zuverlässigkeits- und Überlebenstheorie.
Beispiele für Exponentialverteilungen
Nachdem wir nun die Definition der Exponentialverteilung kennen, schauen wir uns einige Beispiele dieser Art von Verteilung an, um das Konzept besser zu verstehen.
Beispiele für Exponentialverteilung:
- Die Zeit, die zwischen zwei Anrufen in einem Callcenter vergeht.
- Die Zeit, die eine Person warten muss, bis ein kostenloses Taxi auf einer bestimmten Straße vorbeifährt.
- Die Wartezeit, bis ein neuer Kunde ein Geschäft betritt.
- Die Zeit, die zwischen dem Aufrufen einer Webseite durch zwei verschiedene Benutzer vergeht.
- Auf einem Flughafen vergeht die Zeit zwischen dem Start eines Flugzeugs und dem Abflug eines anderen.
Exponentielle Verteilungsformel
Die Dichtefunktionsformel, die die Berechnung einer Exponentialverteilungswahrscheinlichkeit definiert, ist gleich λ multipliziert mit der Zahl e hoch negativ λ mal x.
Mit anderen Worten lautet die Formel zur Berechnung einer Exponentialverteilungswahrscheinlichkeit wie folgt:

👉 Mit dem Rechner unten können Sie die Wahrscheinlichkeit einer Variablen berechnen, die der Exponentialverteilung folgt.
Andererseits lautet die Formel zur Berechnung einer kumulativen Wahrscheinlichkeit der Exponentialverteilung wie folgt:
![]()
Exponentielles Verteilungsdiagramm
In diesem Abschnitt sehen Sie die grafische Darstellung der Dichtefunktion und der Verteilungsfunktion der Exponentialverteilung.
Unten sehen Sie, wie sich der Graph der Dichtefunktion der Exponentialverteilung in Abhängigkeit vom Wert des Parameters λ ändert.
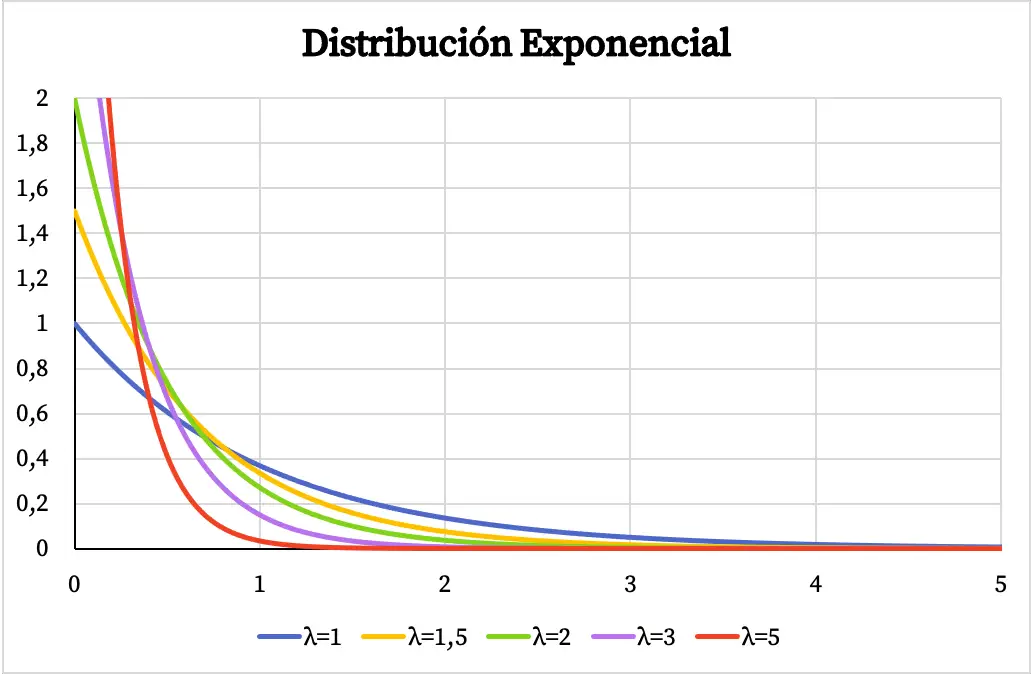
Ebenso hängt die kumulative Wahrscheinlichkeitsfunktion der Exponentialverteilung auch vom Wert des Parameters λ ab, wie Sie in der folgenden Grafik sehen können:
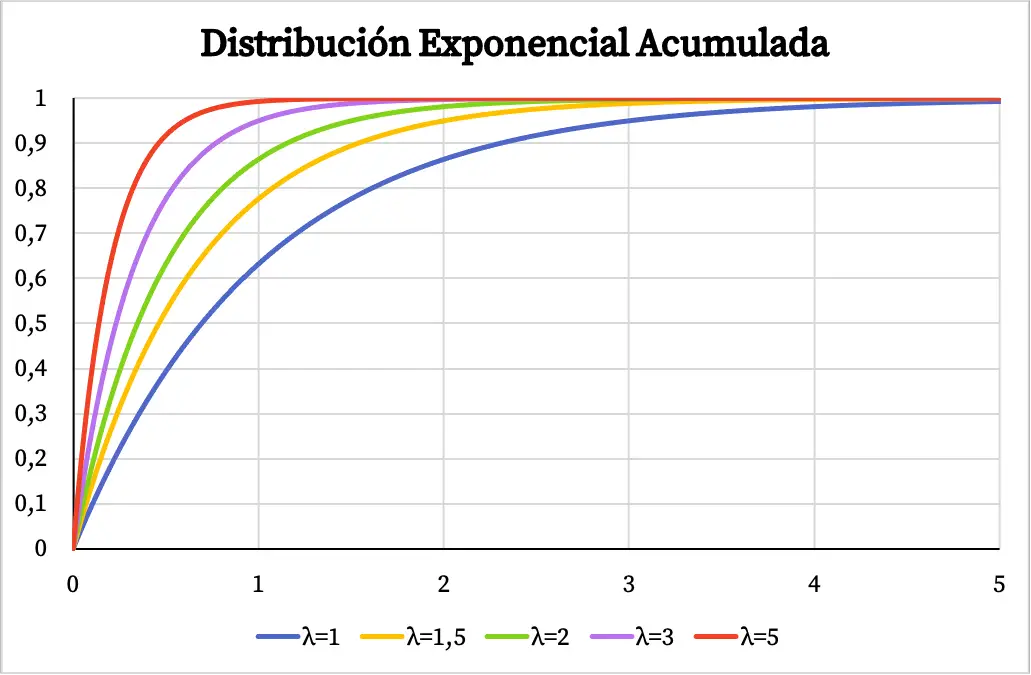
Übung zur Exponentialverteilung gelöst
- Im Durchschnitt greifen λ=1 Benutzer/Minute auf eine bestimmte Webseite zu. Wie hoch ist die Wahrscheinlichkeit, dass die Zeit zwischen dem Betreten zweier Benutzer 3 Minuten beträgt? Und die Wahrscheinlichkeit, dass sie gleich oder kleiner als 2 Minuten ist?
Die Verteilung, die die Zufallsvariable dieses Problems definiert, ist eine Exponentialverteilung, da wir die Zeit untersuchen, die vom Eintreten eines Ereignisses (dem Eintrag eines Benutzers auf der Webseite) bis zum erneuten Auftreten desselben Ereignisses vergeht.
![]()
Um die Wahrscheinlichkeit zu berechnen, dass zwischen dem Eintrag zweier verschiedener Benutzer eine Zeitspanne von drei Minuten vergeht, müssen wir daher die Dichtefunktionsformel anwenden (siehe oben):
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4eb2d6e5190f313d74831763613683ec_l3.png)
Um andererseits eine kumulative Wahrscheinlichkeit zu bestimmen, müssen wir die Verteilungsfunktionsformel der Exponentialverteilung verwenden:
![Rendered by QuickLaTeX.com \begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5ff6ef636fd31aec708b387669a68b93_l3.png)
Merkmale der Exponentialverteilung
Die Exponentialverteilung weist folgende Merkmale auf:
- Die Exponentialverteilung hat einen charakteristischen Parameter, λ, der angibt, wie oft das untersuchte Phänomen in einem bestimmten Zeitraum voraussichtlich auftritt.
![]()
- Die Exponentialverteilung kann keinen negativen Wert annehmen, daher besteht der Bereich der Exponentialverteilung aus allen reellen Zahlen größer oder gleich Null.
![]()
- Der Mittelwert der Exponentialverteilung ist gleich eins dividiert durch den charakteristischen Parameter λ.
![]()
- Die Varianz der Exponentialverteilung ist das Quadrat ihres Mittelwerts, daher ist die Varianz der Exponentialverteilung äquivalent zu eins über dem Koeffizienten λ im Quadrat.
![]()
- Unabhängig vom Wert von λ ist der Asymmetriekoeffizient der Exponentialverteilung immer gleich 2.
![]()
- Ebenso ist der Kurtosis-Koeffizient jeder Exponentialverteilung immer gleich 9.
![]()
- Die Formel für die Dichtefunktion der Exponentialverteilung lautet:
![]()
- Während die Formel für die kumulative Wahrscheinlichkeitsfunktion der Exponentialverteilung wie folgt lautet:
![]()
- Die Exponentialverteilung ist eine der wenigen Wahrscheinlichkeitsverteilungen mit der Eigenschaft „Nicht genügend Speicher“. Diese Eigenschaft bedeutet, dass das Eintreten eines früheren Ereignisses keinen Einfluss auf die Wahrscheinlichkeit hat, dass dieses Ereignis in der Zukunft eintritt. Beispielsweise hängt bei einer Exponentialverteilung die Wahrscheinlichkeit, dass ein neuer Benutzer in weniger als einer Minute auf eine Webseite zugreift, nicht davon ab, ob ein Benutzer sie gerade betreten hat oder seitdem kein Benutzer sie betreten hat. mehr als zehn Minuten.
![P[X>x+y|X>y]=P[X>x]“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“254″ style=“vertical-align: -5px;“></p>
</p>
<h2 class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6f7c755e5b48eb203c51c97d7bc7ec7d_l3.png) Exponentialverteilungsrechner
Exponentialverteilungsrechner
Geben Sie den Wert des Parameters λ und den Wert von x in den folgenden Rechner ein, um die Wahrscheinlichkeit zu berechnen. Sie müssen die Wahrscheinlichkeit auswählen, die Sie berechnen möchten, und die Zahlen mit dem Punkt als Dezimaltrennzeichen eingeben, zum Beispiel 0,50.