So verwenden sie die exponentialverteilung in excel

Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung, mit der die Zeit modelliert wird, die wir warten müssen, bis ein bestimmtes Ereignis eintritt.

Mit dieser Verteilung können Fragen beantwortet werden wie:

• Wie lange sollte ein Einzelhändler warten, bis ein Kunde sein Geschäft betritt?
• Wie lange funktioniert eine Batterie noch, bevor sie leer ist?
• Wie lange funktioniert ein Computer noch, bevor er kaputt geht?

In jedem Szenario wollen wir berechnen, wie lange wir warten müssen, bis ein bestimmtes Ereignis eintritt. Somit könnte jedes Szenario mithilfe einer Exponentialverteilung modelliert werden.

Wenn eine Zufallsvariable X einer Exponentialverteilung folgt, kann die kumulative Dichtefunktion von X geschrieben werden:

F (x; λ) = 1 – e ^-λx

Gold:

• λ: der Geschwindigkeitsparameter (berechnet als λ = 1/μ)
• e: Eine Konstante, die ungefähr 2,718 entspricht

Um die Wahrscheinlichkeiten im Zusammenhang mit der kumulativen Dichtefunktion der Exponentialverteilung in Excel zu berechnen, können wir die folgende Formel verwenden:

 =EXPON.DIST(x, lambda, cumulative)

Gold:

• x : der Wert der exponentiell verteilten Zufallsvariablen
• Lambda : der Geschwindigkeitsparameter
• kumulativ : ob die kumulative Dichtefunktion verwendet werden soll oder nicht (WAHR oder FALSCH)

Die folgenden Beispiele zeigen, wie diese Formel in der Praxis angewendet werden kann.

Beispiel 1: Zeit bis zum Eintreffen des nächsten Kunden

Durchschnittlich alle zwei Minuten betritt ein neuer Kunde ein Geschäft. Bestimmen Sie nach der Ankunft eines Kunden die Wahrscheinlichkeit, dass in weniger als einer Minute ein neuer Kunde eintrifft.

Lösung: Die durchschnittliche Zeit zwischen Kunden beträgt zwei Minuten. Somit kann der Satz wie folgt berechnet werden:

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Wir können also in Excel die folgende Formel verwenden, um die Wahrscheinlichkeit zu berechnen, dass ein neuer Kunde in weniger als einer Minute ankommt:

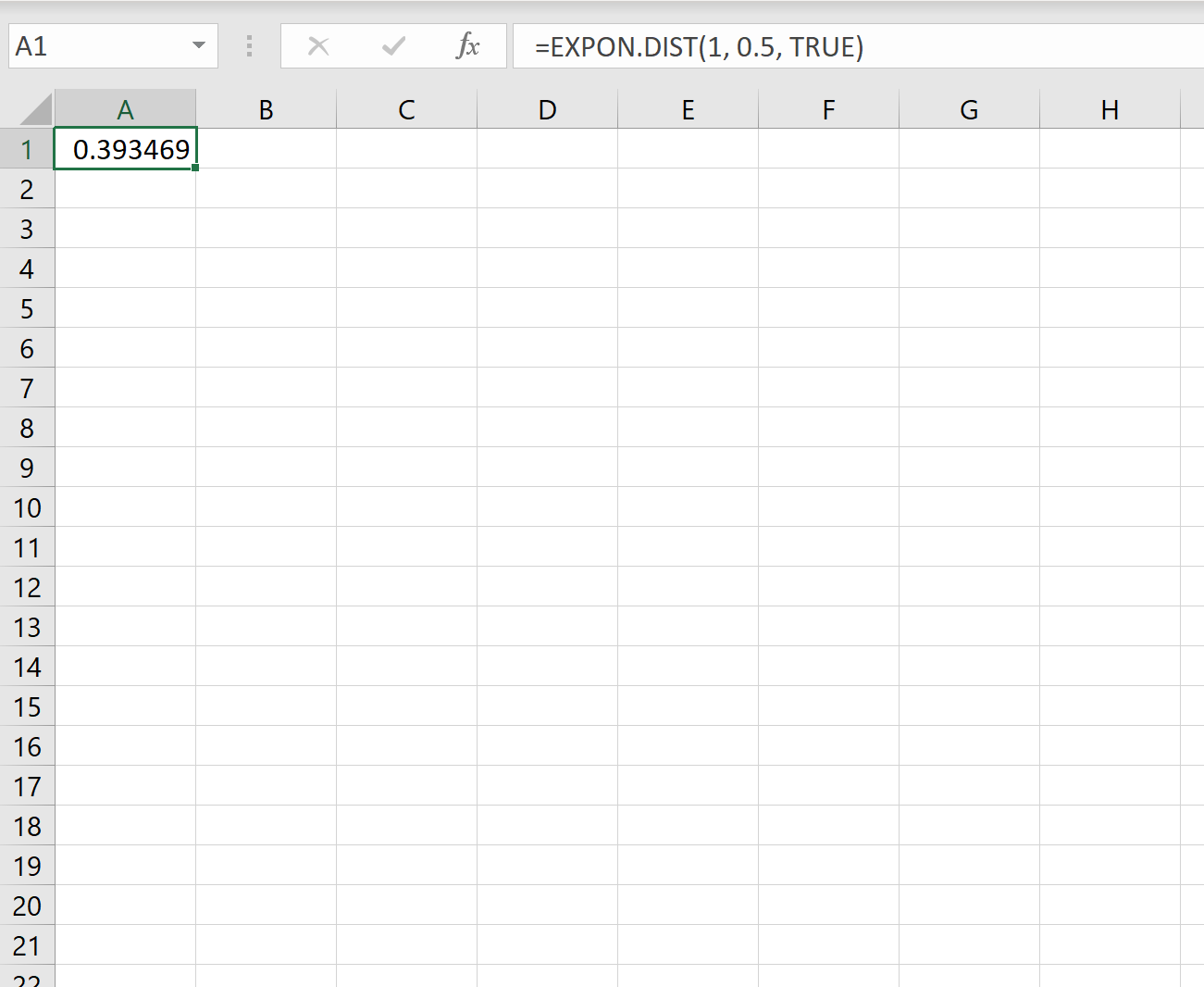
Die Wahrscheinlichkeit, dass wir weniger als eine Minute auf den nächsten Kunden warten müssen, beträgt 0,393469 .

Beispiel 2: Zeit bis zum nächsten Erdbeben

Angenommen, in einer bestimmten Region ereignet sich durchschnittlich alle 400 Tage ein Erdbeben. Bestimmen Sie nach einem Erdbeben die Wahrscheinlichkeit, dass es mehr als 500 Tage dauert, bis das nächste Erdbeben auftritt.

Lösung: Die durchschnittliche Zeit zwischen Erdbeben beträgt 400 Tage. Somit kann der Satz wie folgt berechnet werden:

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Wir können also die folgende Formel in Excel verwenden, um die Wahrscheinlichkeit zu berechnen, dass das nächste Erdbeben weniger als 500 Tage dauern wird:

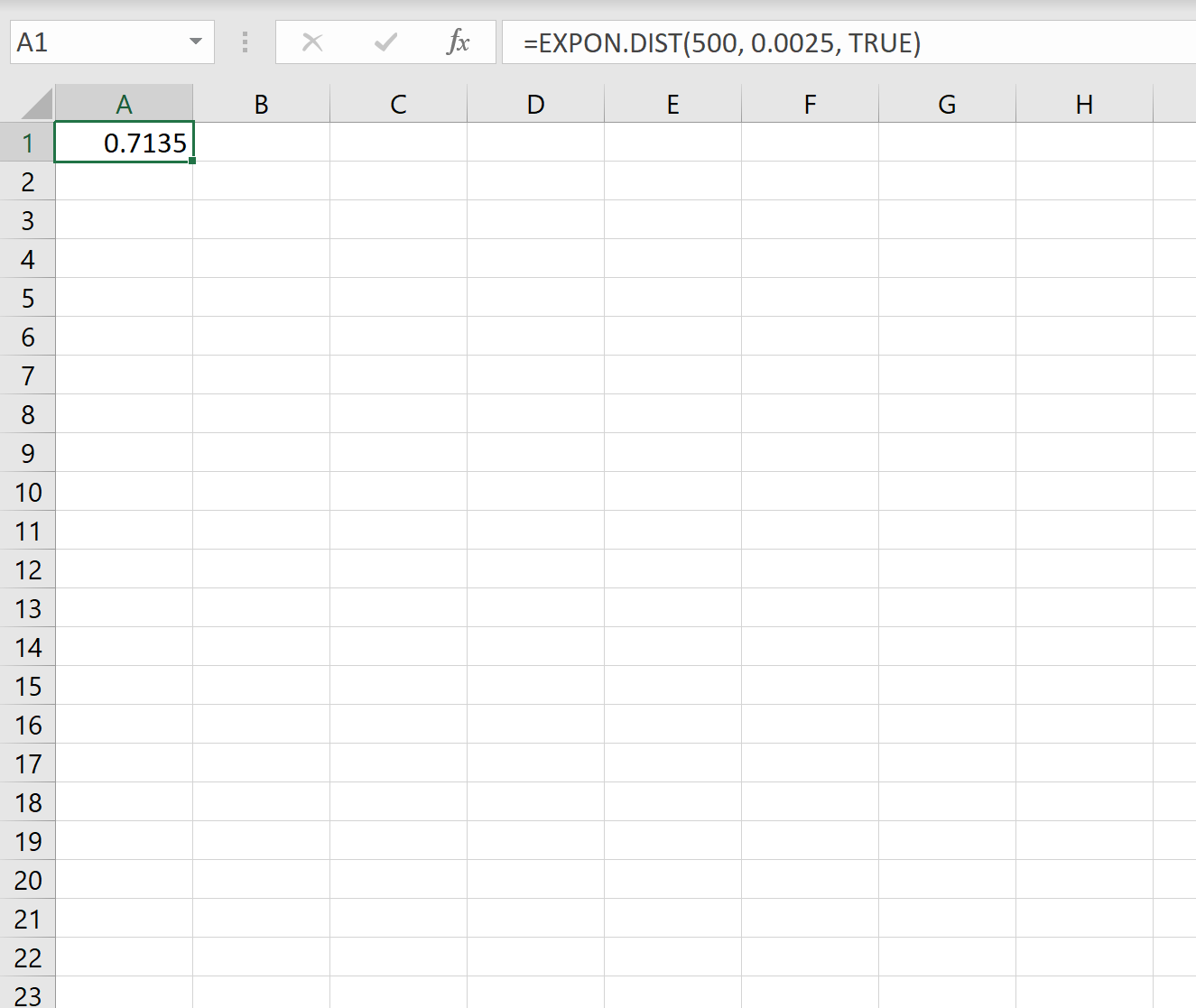
Die Wahrscheinlichkeit, dass das nächste Erdbeben weniger als 500 Tage dauert, beträgt 0,7135.

Die Wahrscheinlichkeit, dass wir mehr als 500 Tage auf das nächste Erdbeben warten müssen, beträgt also 1 – 0,7135 = 0,2865 .

Beispiel 3: Zeit bis zum nächsten Telefonanruf

Nehmen wir an, ein Callcenter erhält durchschnittlich alle 10 Minuten einen neuen Anruf. Bestimmen Sie nach einem Kundenanruf die Wahrscheinlichkeit, dass innerhalb von 10 bis 15 Minuten ein neuer Kunde anruft.

Lösung: Die durchschnittliche Zeit zwischen Anrufen beträgt 10 Minuten. Somit kann der Satz wie folgt berechnet werden:

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Mit der folgenden Formel können wir in Excel also die Wahrscheinlichkeit berechnen, dass der nächste Kunde innerhalb von 10 bis 15 Minuten anruft:

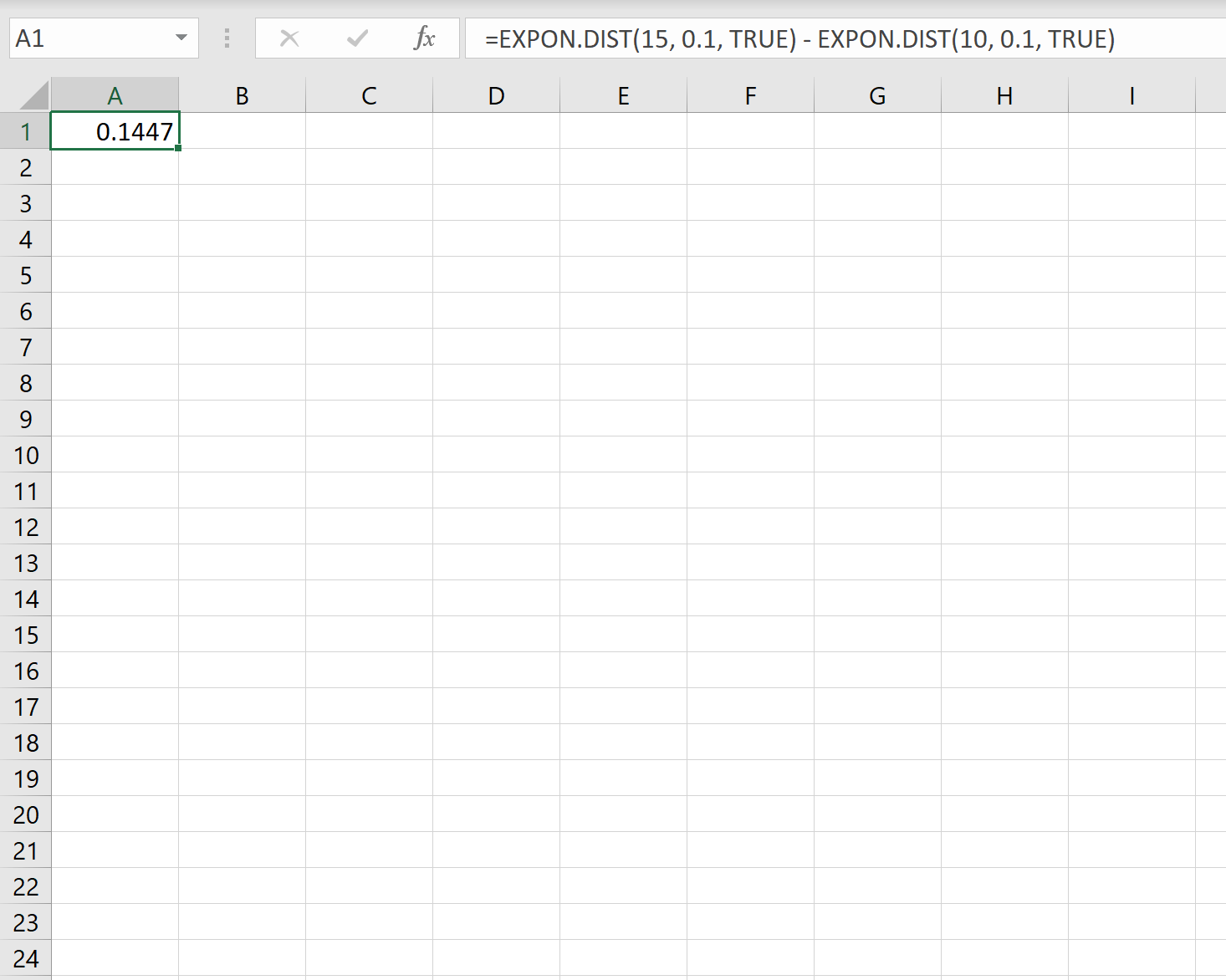
Die Wahrscheinlichkeit, dass ein neuer Kunde innerhalb von 10–15 Minuten anruft. ist 0,1447 .

Zusätzliche Ressourcen

Eine Einführung in die Exponentialverteilung
Die gedächtnislose Eigenschaft der Exponentialverteilung
So zeichnen Sie eine Exponentialverteilung in R auf