Exponentielle regression in r (schritt für schritt)

Die exponentielle Regression ist eine Regressionsart, mit der sich die folgenden Situationen modellieren lassen:

1. Exponentielles Wachstum: Das Wachstum beginnt langsam und beschleunigt sich dann schnell und ohne Grenzen.

2. Exponentieller Zerfall: Der Zerfall beginnt schnell und verlangsamt sich dann, um sich immer mehr dem Nullpunkt zu nähern.

Die Gleichung für ein exponentielles Regressionsmodell hat die folgende Form:

y = ab ^x

Gold:

• y: die Antwortvariable
• x: die Vorhersagevariable
• a, b: die Regressionskoeffizienten, die die Beziehung zwischen x und y beschreiben

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine exponentielle Regression in R durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst gefälschte Daten für zwei Variablen: x und y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

Schritt 2: Visualisieren Sie die Daten

Als Nächstes erstellen wir ein kurzes Streudiagramm, um die Beziehung zwischen x und y zu visualisieren:

 plot(x, y) 

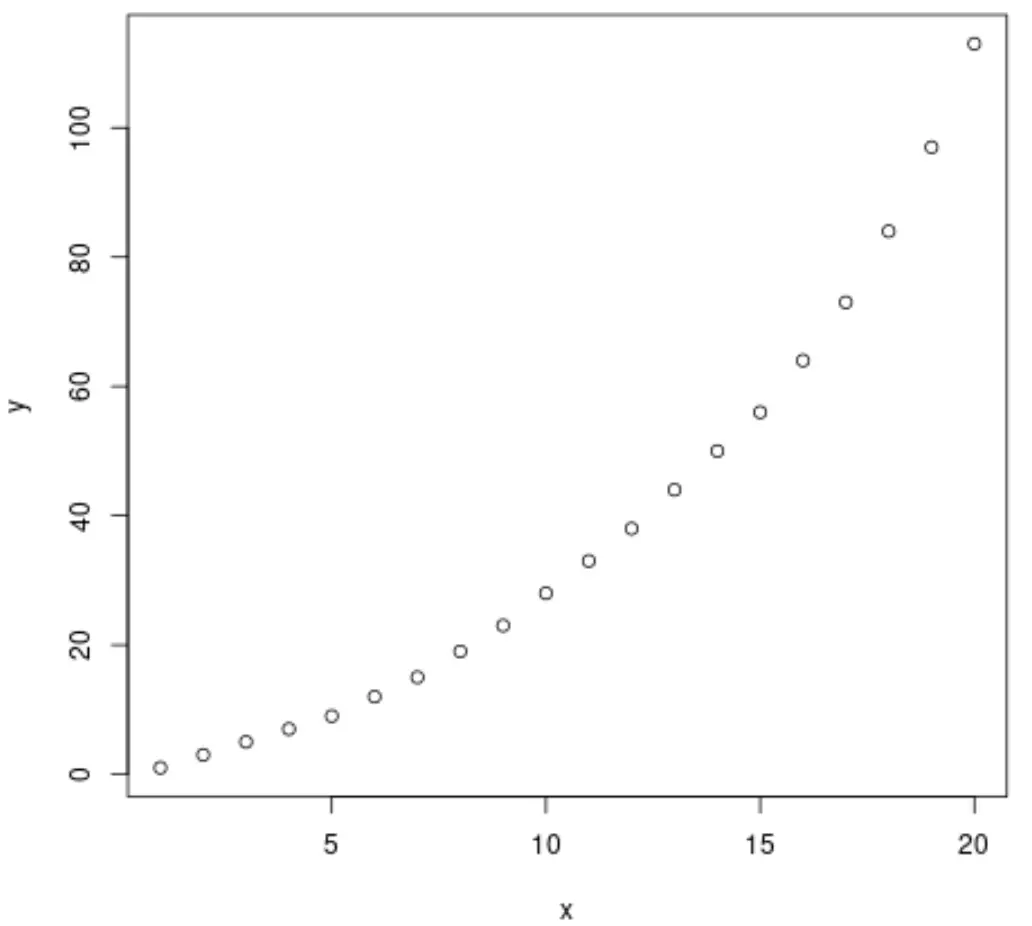
Aus der Grafik können wir erkennen, dass zwischen den beiden Variablen ein klares exponentielles Wachstumsmuster besteht.

Daher erscheint es sinnvoll, eine exponentielle Regressionsgleichung anzuwenden, um die Beziehung zwischen den Variablen zu beschreiben.

Schritt 3: Passen Sie das exponentielle Regressionsmodell an

Als nächstes verwenden wir die Funktion lm() , um ein exponentielles Regressionsmodell anzupassen, wobei wir den natürlichen Logarithmus von y als Antwortvariable und x als Prädiktorvariable verwenden:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

Der Gesamt-F-Wert des Modells beträgt 204 und der entsprechende p-Wert ist extrem niedrig (2,917e-11), was darauf hinweist, dass das Modell insgesamt nützlich ist.

Anhand der Koeffizienten aus der Ausgabetabelle können wir sehen, dass die angepasste exponentielle Regressionsgleichung lautet:

ln(y) = 0,9817 + 0,2041(x)

Wenn wir e auf beide Seiten anwenden, können wir die Gleichung wie folgt umschreiben:

y = 2,6689 * ^1,2264x

Wir können diese Gleichung verwenden, um die Antwortvariable y basierend auf dem Wert der Prädiktorvariablen x vorherzusagen. Wenn zum Beispiel x = 12, dann würden wir vorhersagen, dass y 30,897 wäre:

y = 2,6689 * 1,2264 ^{· 12} = 30,897

Bonus: Fühlen Sie sich frei, diesen Online-Rechner für exponentielle Regression zu verwenden, um die exponentielle Regressionsgleichung für einen bestimmten Prädiktor und eine bestimmte Antwortvariable automatisch zu berechnen.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine quadratische Regression in R durch
So führen Sie eine Polynomregression in R durch