Exponentielle regression in python (schritt für schritt)

Die exponentielle Regression ist eine Art der Regression, mit der sich die folgenden Situationen modellieren lassen:

1. Exponentielles Wachstum: Das Wachstum beginnt langsam und beschleunigt sich dann schnell und ohne Grenzen.

2. Exponentieller Zerfall: Der Zerfall beginnt schnell und verlangsamt sich dann, um sich immer mehr dem Nullpunkt zu nähern.

Die Gleichung für ein exponentielles Regressionsmodell hat die folgende Form:

y = ab ^x

Gold:

• y: die Antwortvariable
• x: die Vorhersagevariable
• a, b: die Regressionskoeffizienten, die die Beziehung zwischen x und y beschreiben

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie man eine exponentielle Regression in Python durchführt.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst gefälschte Daten für zwei Variablen: x und y :

 import numpy as np

x = np. arange (1, 21, 1)
y = np. array ([1, 3, 5, 7, 9, 12, 15, 19, 23, 28,
              33, 38, 44, 50, 56, 64, 73, 84, 97, 113])

Schritt 2: Visualisieren Sie die Daten

Als Nächstes erstellen wir ein kurzes Streudiagramm, um die Beziehung zwischen x und y zu visualisieren:

 import matplotlib. pyplot as plt

plt. scatter (x,y)
plt. show () 

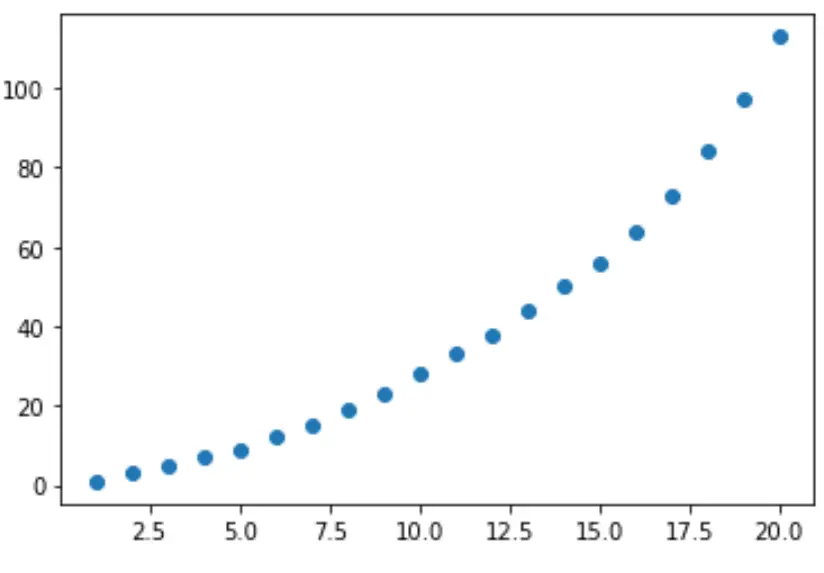
Aus der Grafik können wir erkennen, dass zwischen den beiden Variablen ein klares exponentielles Wachstumsmuster besteht.

Daher erscheint es sinnvoll, anstelle eines linearen Regressionsmodells eine exponentielle Regressionsgleichung zur Beschreibung der Beziehung zwischen Variablen anzuwenden.

Schritt 3: Passen Sie das exponentielle Regressionsmodell an

Als nächstes verwenden wir die Funktion polyfit() , um ein exponentielles Regressionsmodell anzupassen, wobei wir den natürlichen Logarithmus von y als Antwortvariable und x als Prädiktorvariable verwenden:

 #fit the model
fit = np. polyfit (x, np. log (y), 1)

#view the output of the model
print(fit)

[0.2041002 0.98165772]

Basierend auf dem Ergebnis kann die angepasste exponentielle Regressionsgleichung wie folgt geschrieben werden:

ln(y) = 0,9817 + 0,2041(x)

Wenn wir e auf beide Seiten anwenden, können wir die Gleichung wie folgt umschreiben:

y = 2,6689 * ^1,2264x

Wir können diese Gleichung verwenden, um die Antwortvariable y basierend auf dem Wert der Prädiktorvariablen x vorherzusagen. Wenn zum Beispiel x = 12, dann würden wir vorhersagen, dass y 30,897 wäre:

y = 2,6689 * 1,2264 ^{· 12} = 30,897

Bonus: Fühlen Sie sich frei, diesen Online-Rechner für exponentielle Regression zu verwenden, um die exponentielle Regressionsgleichung für einen bestimmten Prädiktor und eine bestimmte Antwortvariable automatisch zu berechnen.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in Python durch
So führen Sie eine Polynomregression in Python durch
So führen Sie eine Quantilregression in Python durch