So verwenden sie die exponentialverteilung in python

Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung, mit der die Zeit modelliert wird, die wir warten müssen, bis ein bestimmtes Ereignis eintritt.

Wenn eine Zufallsvariable X einer Exponentialverteilung folgt, kann die kumulative Verteilungsfunktion von X geschrieben werden:

F (x; λ) = 1 – e ^-λx

Gold:

• λ: der Geschwindigkeitsparameter (berechnet als λ = 1/μ)
• e: Eine Konstante, die ungefähr 2,718 entspricht

In diesem Tutorial wird erklärt, wie Sie die Exponentialverteilung in Python verwenden.

So generieren Sie eine Exponentialverteilung

Sie können die Funktion expon.rvs(scale, size) aus der SciPy-Bibliothek in Python verwenden, um Zufallswerte aus einer Exponentialverteilung mit einem bestimmten Ratenparameter und einer bestimmten Stichprobengröße zu generieren:

 from scipy. stats import expo

#generate random values from exponential distribution with rate=40 and sample size=10
expon. rvs (scale= 40 , size= 10 )

array([116.5368323 , 67.23514699, 12.00399043, 40.74580584,
        34.60922432, 2.68266663, 22.70459831, 97.66661811,
         6.64272914, 46.15547298])

Hinweis : Die vollständige Dokumentation der SciPy-Bibliothek finden Sie hier .

So berechnen Sie Wahrscheinlichkeiten mithilfe einer Exponentialverteilung

Nehmen wir an, dass die durchschnittliche Anzahl der Minuten zwischen den Ausbrüchen eines bestimmten Geysirs 40 Minuten beträgt. Wie wahrscheinlich ist es, dass wir weniger als 50 Minuten auf einen Ausbruch warten müssen?

Um dieses Problem zu lösen, müssen wir zunächst den Geschwindigkeitsparameter berechnen:

• λ = 1/µ
• λ = 1/40
• λ = 0,025

Wir können λ = 0,025 und x = 50 in die CDF-Formel einsetzen:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

Die Wahrscheinlichkeit, dass wir weniger als 50 Minuten auf den nächsten Ausbruch warten müssen, beträgt 0,7135 .

Wir können die Funktion expon.cdf() von SciPy verwenden, um dieses Problem in Python zu lösen:

 from scipy. stats import expo

#calculate probability that x is less than 50 when mean rate is 40
expon. cdf (x=50, scale=40)

0.7134952031398099

Die Wahrscheinlichkeit, dass wir weniger als 50 Minuten auf den nächsten Ausbruch warten müssen, beträgt 0,7135 .

Dies entspricht dem von uns manuell berechneten Wert.

So zeichnen Sie eine Exponentialverteilung auf

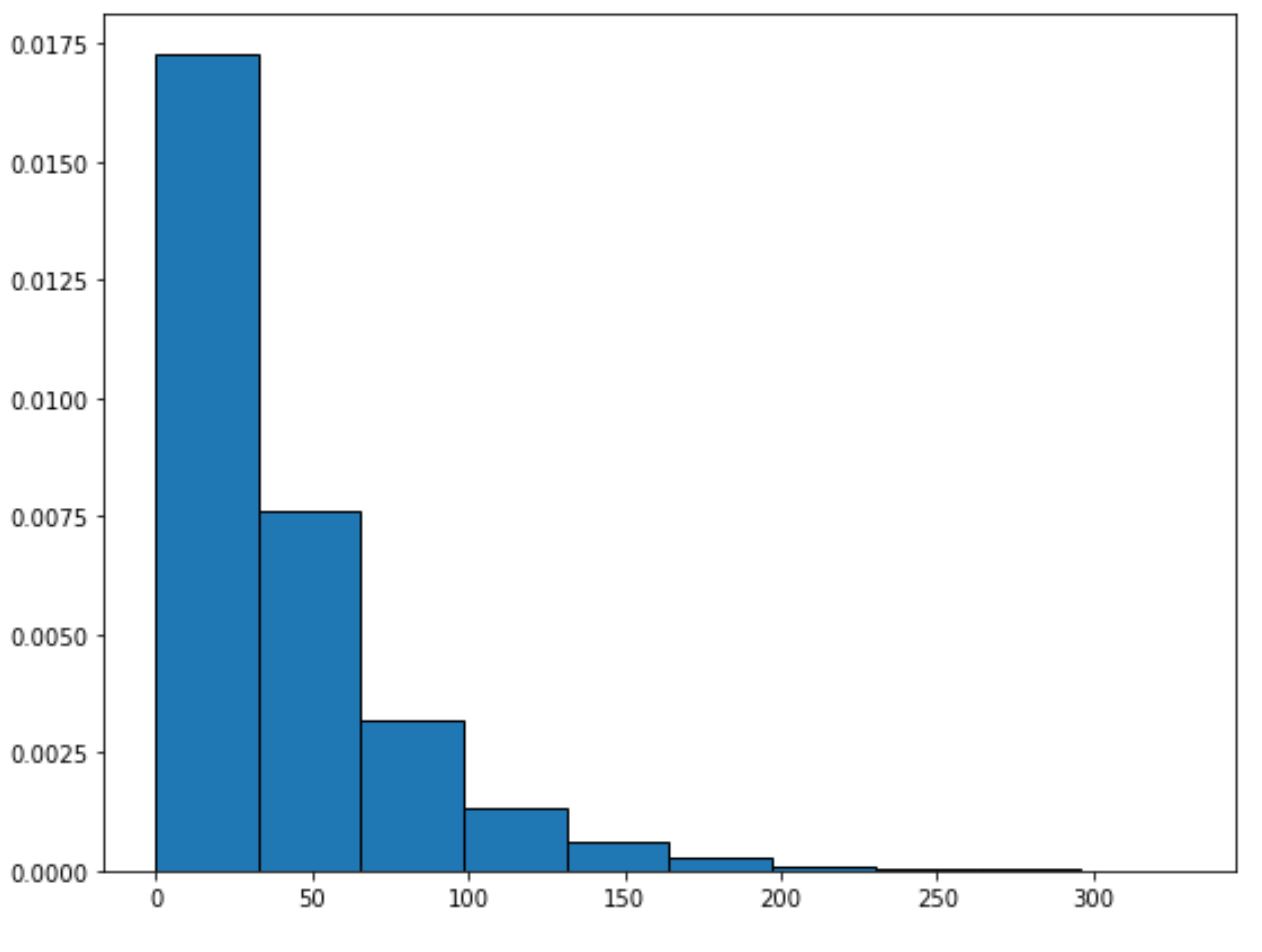
Sie können die folgende Syntax verwenden, um eine Exponentialverteilung mit einem bestimmten Ratenparameter darzustellen:

 from scipy. stats import expo
import matplotlib. pyplot as plt

#generate exponential distribution with sample size 10000
x = expon. rvs (scale= 40 ,size= 10000 )

#create plot of exponential distribution
plt. hist (x, density= True , edgecolor=' black ')

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie andere gängige Distributionen in Python verwenden:

So verwenden Sie die Poisson-Verteilung in Python
So verwenden Sie die t-Verteilung in Python
So verwenden Sie eine einheitliche Verteilung in Python