So extrahieren sie residuen aus der funktion lm() in r

Sie können die folgende Syntax verwenden, um Residuen aus der Funktion lm() in R zu extrahieren:

 fit$residuals

In diesem Beispiel wird davon ausgegangen, dass wir die Funktion lm() zum Anpassen eines linearen Regressionsmodells verwendet und die Ergebnisse fit genannt haben.

Das folgende Beispiel zeigt, wie diese Syntax in der Praxis verwendet wird.

Verwandt: So extrahieren Sie das R-Quadrat aus der Funktion lm() in R

Beispiel: So extrahieren Sie Residuen aus lm() in R

Angenommen, wir haben den folgenden Datenrahmen in R, der Informationen über die gespielten Minuten, die Gesamtzahl der Fouls und die Gesamtpunktzahl von 10 Basketballspielern enthält:

 #create data frame
df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40),
                 fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1),
                 points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30))

#view data frame
df

   minutes fouls points
1 5 5 6
2 10 5 8
3 13 3 8
4 14 4 7
5 20 2 14
6 22 1 10
7 26 3 22
8 34 2 24
9 38 1 28
10 40 1 30

Angenommen, wir möchten das folgende multiple lineare Regressionsmodell anpassen:

Punkte = β ₀ + β ₁ (Minuten) + β ₂ (Fouls)

Wir können die Funktion lm() verwenden, um dieses Regressionsmodell anzupassen:

 #fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)

Anschließend können wir fit$residuals eingeben, um die Residuen aus dem Modell zu extrahieren:

 #extract residuals from model
fit$residuals

         1 2 3 4 5 6 7 
 2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786 
         8 9 10 
-1.7048752 0.5692404 0.6144057

Da unsere Datenbank insgesamt 10 Beobachtungen enthielt, gibt es 10 Residuen – eines für jede Beobachtung.

Zum Beispiel:

• Die erste Beobachtung hat ein Residuum von 2.089 .
• Die zweite Beobachtung hat ein Residuum von -0,798 .
• Die dritte Beobachtung hat ein Residuum von 0,637 .

Und so weiter.

Wenn wir möchten, können wir dann ein Diagramm der Residuen gegenüber den angepassten Werten erstellen:

 #store residuals in variable
res <- fit$residuals

#produce residual vs. fitted plot
plot(fitted(fit), res)

#add a horizontal line at 0 
abline(0,0)

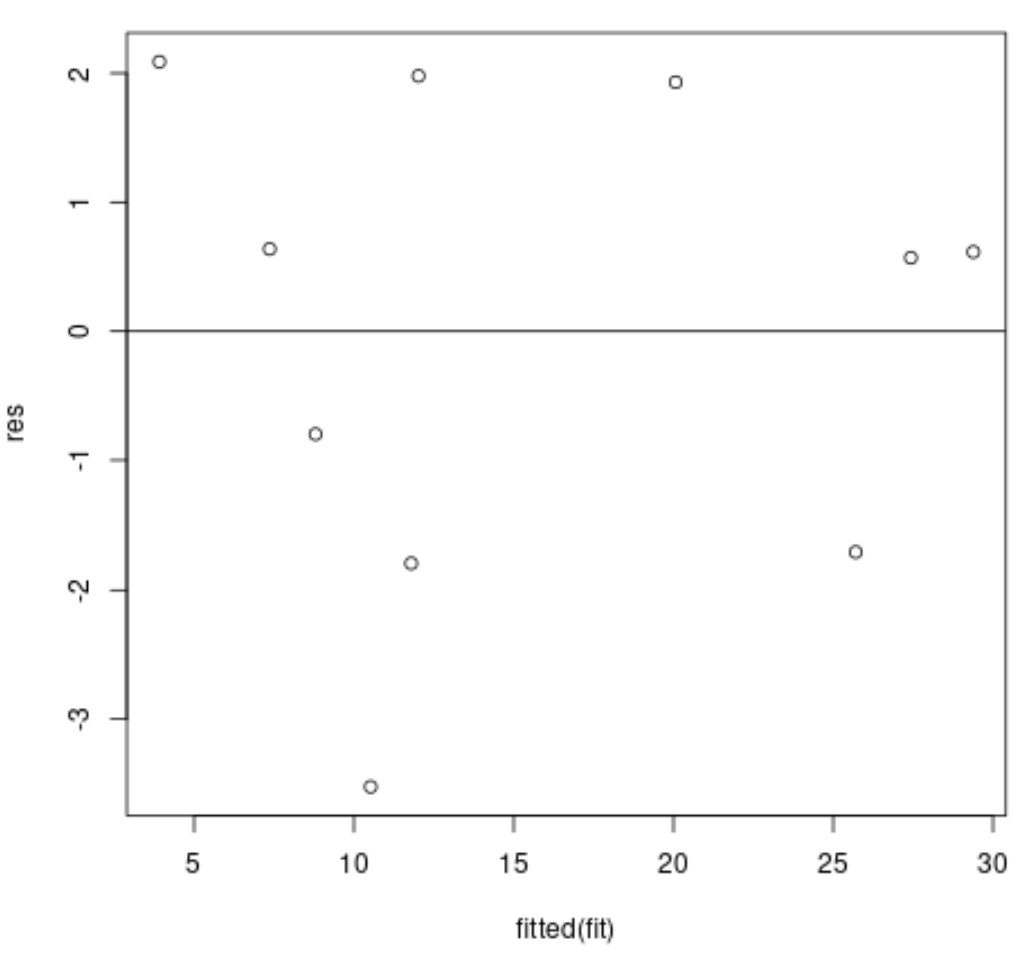
Die x-Achse zeigt die angepassten Werte und die y-Achse zeigt die Residuen an.

Im Idealfall sollten die Residuen zufällig um Null herum verstreut sein und kein klares Muster aufweisen, um sicherzustellen, dass die Homoskedastizitätsannahme erfüllt ist.

Im obigen Residuendiagramm können wir sehen, dass die Residuen scheinbar zufällig um Null herum verstreut sind und kein klares Muster aufweisen, was bedeutet, dass die Annahme der Homoskedastizität wahrscheinlich erfüllt ist.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in R ausführen:

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So erstellen Sie ein Residuendiagramm in R