So erstellen sie ein bland-altman-diagramm in r (schritt für schritt)

Ein Bland-Altman-Diagramm wird verwendet, um Messunterschiede zwischen zwei verschiedenen Instrumenten oder zwei verschiedenen Messtechniken zu visualisieren.

Dies ist nützlich, um festzustellen, wie ähnlich zwei Instrumente oder Techniken bei der Messung desselben Konzepts sind.

Dieses Tutorial bietet ein schrittweises Beispiel für die Erstellung eines Bland-Altman-Diagramms in R.

Schritt 1: Erstellen Sie die Daten

Angenommen, ein Biologe verwendet zwei verschiedene Instrumente (A und B), um das Gewicht derselben Gruppe von 20 verschiedenen Fröschen in Gramm zu messen.

Wir erstellen den folgenden Datenrahmen in R, der das Gewicht jedes Frosches darstellt, gemessen von jedem Instrument:

 #create data
df <- data. frame (A=c(5, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9,
                     10, 11, 13, 14, 14, 15, 18, 22, 25),
                 B=c(4, 4, 5, 5, 5, 7, 8, 6, 9, 7, 7, 11,
                     13, 13, 12, 13, 14, 19, 19, 24))

#view first six rows of data
head(df)

  AB
1 5 4
2 5 4
3 5 5
4 6 5
5 6 5
6 7 7

Schritt 2: Berechnen Sie die Differenz der Messungen

Als nächstes erstellen wir zwei neue Spalten im Datenrahmen, die die durchschnittliche Messung jedes Frosches sowie die Differenz der Messungen enthalten:

 #create new column for average measurement
df$avg <- rowMeans(df) 

#create new column for difference in measurements
df$diff <- df$A - df$B

#view first six rows of data
head(df)

  AB avg diff
1 5 4 4.5 1
2 5 4 4.5 1
3 5 5 5.0 0
4 6 5 5.5 1
5 6 5 5.5 1
6 7 7 7.0 0

Schritt 3: Berechnen Sie die mittlere Differenz und das Konfidenzintervall

Als nächstes berechnen wir die durchschnittliche Differenz der Messungen zwischen den beiden Instrumenten sowie die Ober- und Untergrenze des 95 %-Konfidenzintervalls für die durchschnittliche Differenz:

 #find average difference
mean_diff <- mean(df$diff)

mean_diff

[1] 0.5

#find lower 95% confidence interval limits
lower <- mean_diff - 1.96*sd(df$diff)

lower

[1] -1.921465

#find upper 95% confidence interval limits
upper <- mean_diff + 1.96*sd(df$diff)

upper

[1] 2.921465

Die mittlere Differenz beträgt 0,5 und das 95 %-Konfidenzintervall für die mittlere Differenz beträgt [-1,921, 2,921] .

Schritt 4: Erstellen Sie das Bland-Altman-Diagramm

Als Nächstes verwenden wir den folgenden Code, um mit dem Datenvisualisierungspaket ggplot2 ein Bland-Altman-Diagramm zu erstellen:

 #load ggplot2
library (ggplot2)

#create Bland-Altman plot
ggplot(df, aes (x = avg, y = diff)) +
  geom_point(size=2) +
  geom_hline(yintercept = mean_diff) +
  geom_hline(yintercept = lower, color = " red ", linetype=" dashed ") +
  geom_hline(yintercept = upper, color = " red ", linetype=" dashed ") +
  ggtitle(" Bland-Altman Plot ") +
  ylab(" Difference Between Measurements ") +
  xlab(" Average Measurement ") 

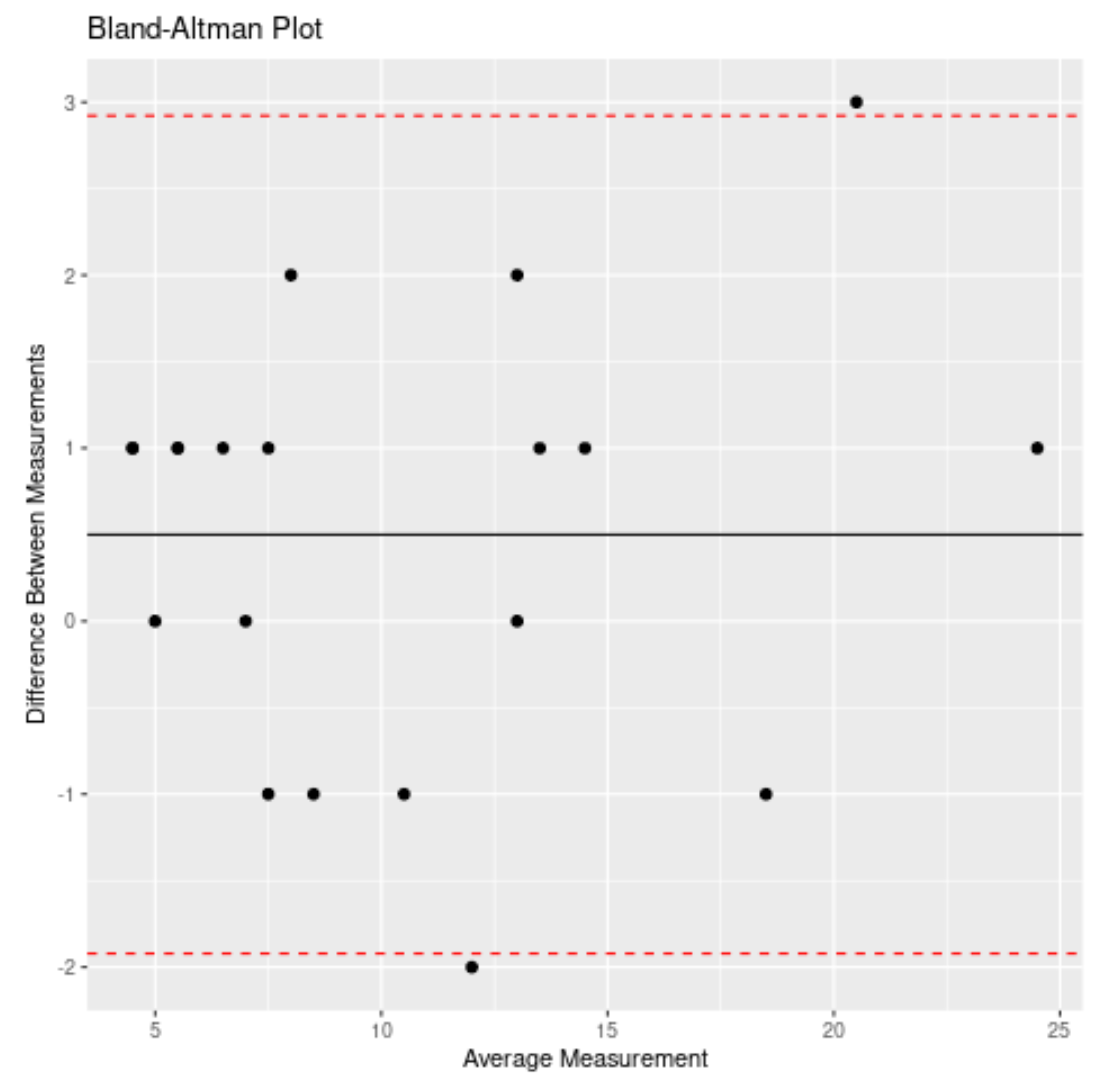
Die x-Achse des Diagramms zeigt die durchschnittliche Messung der beiden Instrumente und die y-Achse zeigt den Unterschied in den Messungen zwischen den beiden Instrumenten.

Die schwarze Linie stellt die mittlere Differenz der Messungen zwischen den beiden Instrumenten dar, während die beiden roten gepunkteten Linien die Grenzen des 95 %-Konfidenzintervalls für die mittlere Differenz darstellen.