Was ist eine faktorielle anova? (definition & #038; beispiel)

Eine faktorielle ANOVA ist jede ANOVA („Varianzanalyse“), die zwei oder mehr unabhängige Faktoren und eine einzelne Antwortvariable verwendet.

Diese Art von ANOVA sollte immer dann verwendet werden, wenn Sie verstehen möchten, wie sich zwei oder mehr Faktoren auf eine Antwortvariable auswirken und ob es einen Interaktionseffekt zwischen den Faktoren auf die Antwortvariable gibt oder nicht.

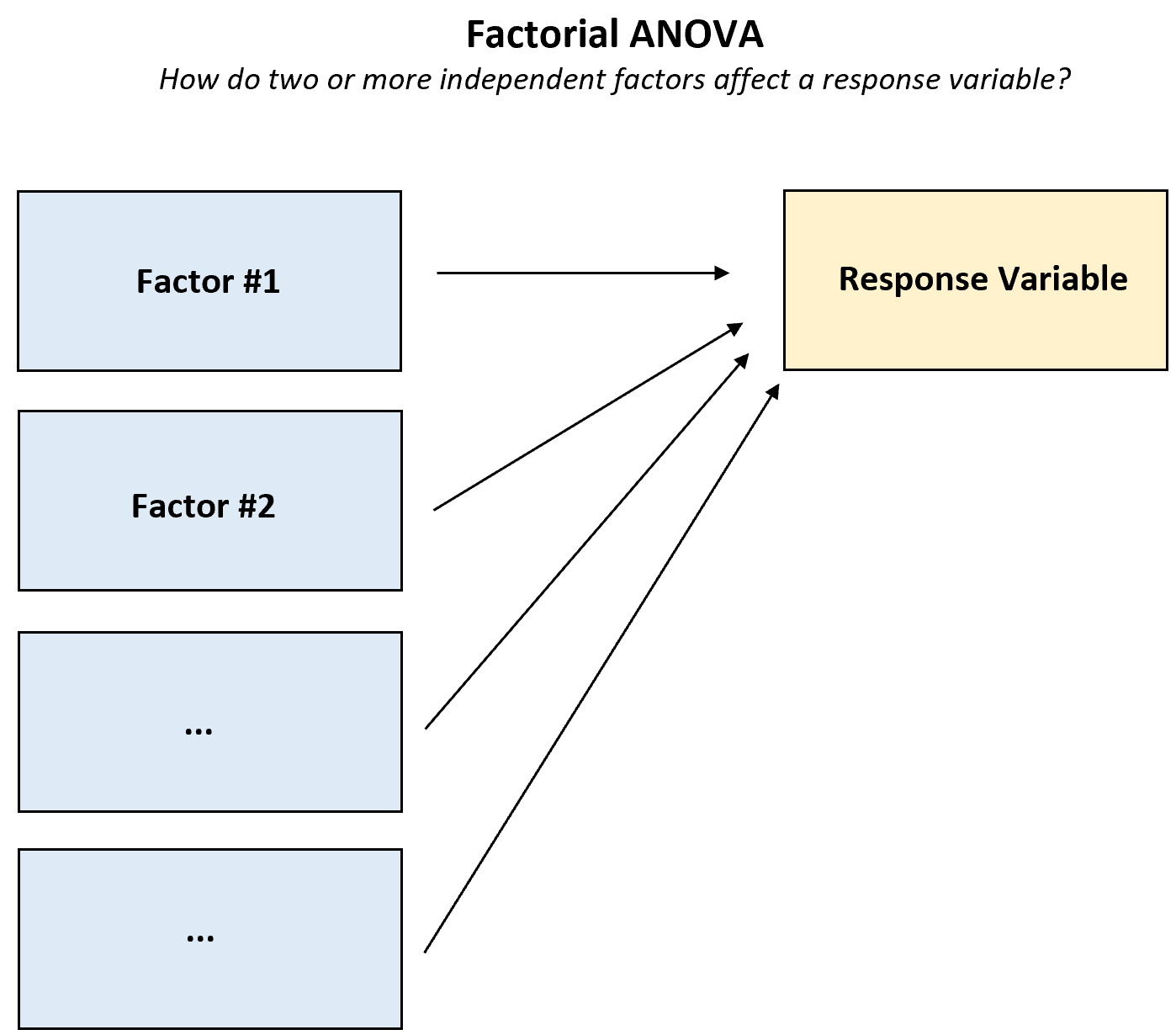
Dieses Tutorial bietet mehrere Beispiele für Situationen, in denen eine faktorielle ANOVA verwendet werden kann, sowie ein schrittweises Beispiel für die Durchführung einer faktoriellen ANOVA.

Hinweis: Eine zweifaktorielle ANOVA ist eine Art faktorielle ANOVA.

Beispiele für die Verwendung einer faktoriellen ANOVA

Eine faktorielle ANOVA könnte in jeder der folgenden Situationen verwendet werden.

Beispiel 1: Pflanzenwachstum

Ein Botaniker möchte verstehen, wie sich Sonneneinstrahlung und Bewässerungshäufigkeit auf das Pflanzenwachstum auswirken. Sie pflanzt 100 Samen und lässt sie drei Monate lang unter unterschiedlichen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach drei Monaten zeichnet sie die Höhe jeder Pflanze auf.

In diesem Fall hat es die folgenden Variablen:

• Antwortvariable: Pflanzenwachstum
• Faktoren: Sonneneinstrahlung, Bewässerungshäufigkeit

Und sie möchte folgende Fragen beantworten:

• Beeinflusst Sonneneinstrahlung das Pflanzenwachstum?
• Beeinflusst die Bewässerungshäufigkeit das Pflanzenwachstum?
• Gibt es einen Wechselwirkungseffekt zwischen Sonneneinstrahlung und Bewässerungshäufigkeit?

Sie könnte für diese Analyse eine faktorielle ANOVA verwenden, weil sie verstehen möchte, wie sich zwei Faktoren auf eine einzelne Antwortvariable auswirken.

Beispiel 2: Prüfungsergebnisse

Ein Professor möchte verstehen, wie sich die Unterrichtszeit und die Lehrmethode auf die Prüfungsergebnisse auswirken. Es verwendet zwei unterschiedliche Lehrmethoden und zwei unterschiedliche Unterrichtszeiten (früher Morgen und früher Nachmittag) und erfasst die durchschnittlichen Prüfungsergebnisse jedes Studierenden am Ende des Semesters.

In diesem Fall hat es die folgenden Variablen:

• Antwortvariable: Prüfungsergebnis
• Faktoren: Lehrmethode, Unterrichtszeit

Und er möchte folgende Fragen beantworten:

• Beeinflusst die Lehrmethode die Prüfungsergebnisse?
• Beeinflusst die Unterrichtszeit die Prüfungsergebnisse?
• Gibt es einen Interaktionseffekt zwischen Lehrmethode und Unterrichtszeit?

Er könnte für diese Analyse eine faktorielle ANOVA verwenden, weil er verstehen möchte, wie sich zwei Faktoren auf eine einzelne Antwortvariable auswirken.

Beispiel 3: Jahreseinkommen

Ein Wirtschaftswissenschaftler sammelt Daten, um zu verstehen, wie sich das Bildungsniveau (Abitur, Hochschulabschluss, Hochschulabschluss), der Familienstand (ledig, geschieden, verheiratet) und die Region (Nord, Ost, Süd, West) auf das Jahreseinkommen auswirken.

In diesem Fall hat es die folgenden Variablen:

• Antwortvariable: Jahreseinkommen
• Faktoren: Bildungsniveau, Familienstand, Region

Und er möchte folgende Fragen beantworten:

• Beeinflusst das Bildungsniveau das Einkommen?
• Beeinflusst der Familienstand das Einkommen?
• Beeinflusst die Region das Einkommen?
• Gibt es einen Wechselwirkungseffekt zwischen diesen drei unabhängigen Faktoren?

Er könnte für diese Analyse eine faktorielle ANOVA verwenden, weil er verstehen möchte, wie sich drei Faktoren auf eine einzelne Antwortvariable auswirken.

Schritt-für-Schritt-Beispiel einer faktoriellen ANOVA

Ein Botaniker möchte wissen, ob die Sonneneinstrahlung und die Häufigkeit des Gießens das Pflanzenwachstum beeinflussen. Sie pflanzt 40 Samen und lässt sie zwei Monate lang unter unterschiedlichen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach zwei Monaten zeichnet sie die Höhe jeder Pflanze auf.

Die Ergebnisse sind unten dargestellt:

Wir können sehen, dass in jeder Kombination von Bedingungen fünf Pflanzen gewachsen sind.

Beispielsweise wurden fünf Pflanzen mit täglicher Bewässerung und ohne Sonnenlicht gezüchtet und ihre Höhen betrugen nach zwei Monaten 4,8 Zoll, 4,4 Zoll, 3,2 Zoll, 3,9 Zoll und 4,4 Zoll:

Mit diesen Daten führt der Botaniker eine faktorielle ANOVA in Excel durch und erhält folgendes Ergebnis:

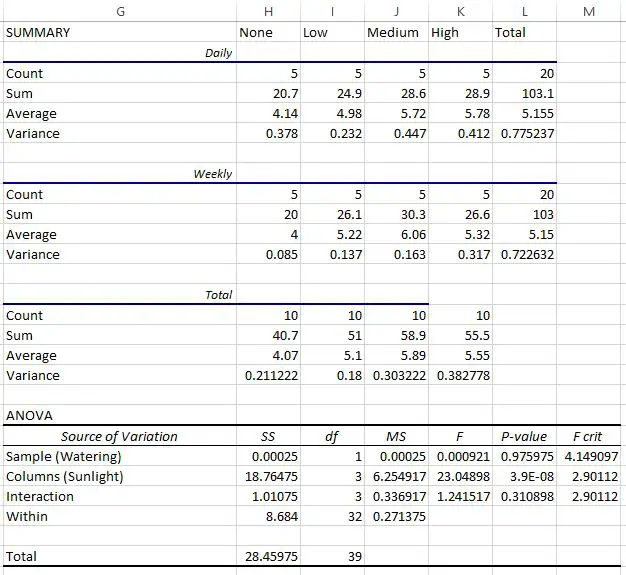
Die letzte Tabelle zeigt das Ergebnis der faktoriellen ANOVA:

• Der p-Wert für die Wechselwirkung zwischen Bewässerungshäufigkeit und Sonneneinstrahlung betrug 0,310898 . Dies ist auf dem Alpha-Niveau von 0,05 statistisch nicht signifikant.
• Der p-Wert für die Bewässerungshäufigkeit betrug 0,975975 . Dies ist auf dem Alpha-Niveau von 0,05 statistisch nicht signifikant.
• Der p-Wert für Sonneneinstrahlung betrug 3,9E-8 (0,000000039) . Dies ist statistisch signifikant bei einem Alpha-Wert von 0,05.

Wir können daraus schließen, dass die Sonneneinstrahlung der einzige Faktor ist, der einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat.

Wir können auch den Schluss ziehen, dass es keinen Wechselwirkungseffekt zwischen Sonneneinstrahlung und Bewässerungshäufigkeit gibt und dass die Bewässerungshäufigkeit keinen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat. Pflanzen.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu ANOVA-Modellen:

Eine Einführung in die einfaktorielle ANOVA
Eine Einführung in die zweifaktorielle ANOVA
Eine Einführung in die ANOVA mit wiederholten Messungen
Die Unterschiede zwischen ANOVA, ANCOVA, MANOVA und MANCOVA