So ermitteln sie die fehlerquote auf einem ti-84-rechner

In der Statistik verwenden wir häufig Konfidenzintervalle , um den Wert eines Populationsparameters mit einem bestimmten Konfidenzniveau zu schätzen.

Jedes Konfidenzintervall hat die folgende Form:

Konfidenzintervall = [untere Grenze, obere Grenze]

Die Fehlerspanne entspricht der halben Breite des gesamten Konfidenzintervalls.

Angenommen, wir haben das folgende Konfidenzintervall für einen Bevölkerungsanteil:

95 %-Konfidenzintervall = [0,34, 0,46]

Die Breite des Konfidenzintervalls beträgt 0,46 – 0,34 = 0,12. Die Fehlerspanne beträgt die Hälfte der Breite, also 0,12/2 = 0,6 .

Die folgenden Beispiele zeigen, wie die Fehlerspanne für Konfidenzintervalle auf einem TI-84-Rechner berechnet wird.

Beispiel 1: Fehlerspanne für einen Bevölkerungsdurchschnitt

Angenommen, Sie möchten die Fehlerspanne für ein 95 %-Konfidenzintervall berechnen, das einen Grundgesamtheitsmittelwert mit den folgenden Informationen schätzt:

• x : 30,4
• s: 4,5
• n: 50

Um das Konfidenzintervall für den Grundgesamtheitsmittelwert zu berechnen, drücken Sie STAT , scrollen Sie dann nach rechts und drücken Sie TESTS . Drücken Sie dann 7 :

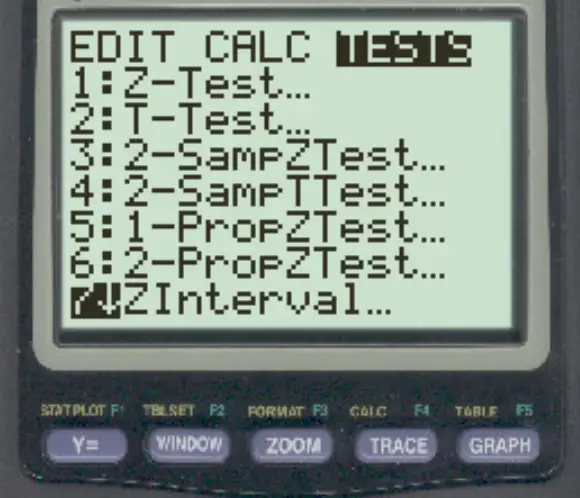
Geben Sie als Nächstes die folgenden Informationen ein und klicken Sie auf BERECHNEN :

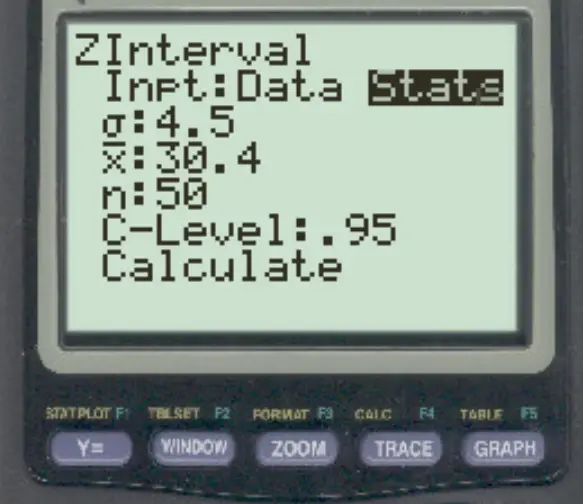
Das Konfidenzintervall beträgt (29,153, 31,647) :

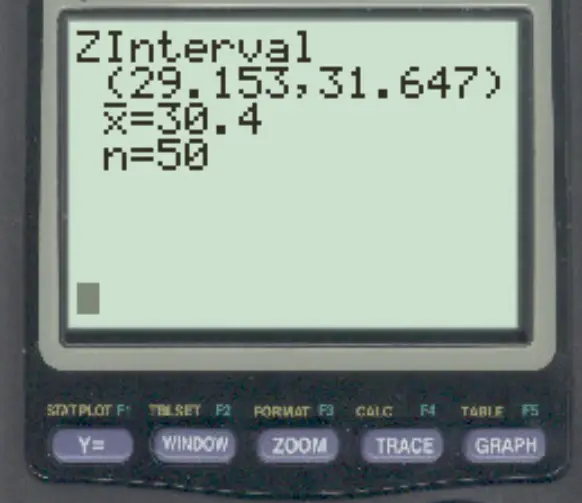
Die Fehlerspanne würde der halben Breite dieses Konfidenzintervalls entsprechen, d. h.:

Fehlerquote: (31,647 – 29,153) / 2 = 1,247

Beispiel 2: Fehlerspanne für einen Bevölkerungsanteil

Angenommen, Sie möchten die Fehlerspanne für ein 95 %-Konfidenzintervall berechnen, das einen Bevölkerungsanteil mit den folgenden Informationen schätzt:

• x: 42
• n: 90

Um das Konfidenzintervall für den Grundgesamtheitsmittelwert zu berechnen, drücken Sie STAT , scrollen Sie dann nach rechts und drücken Sie TESTS . Scrollen Sie dann nach unten, tippen Sie auf 1-PropZInt und drücken Sie die EINGABETASTE .

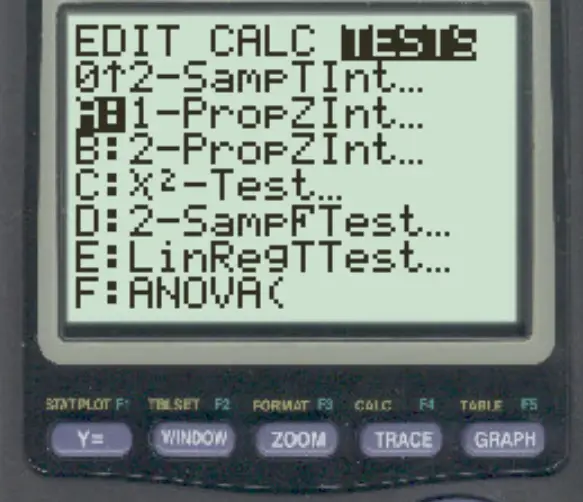
Geben Sie als Nächstes die folgenden Informationen ein und klicken Sie auf BERECHNEN :

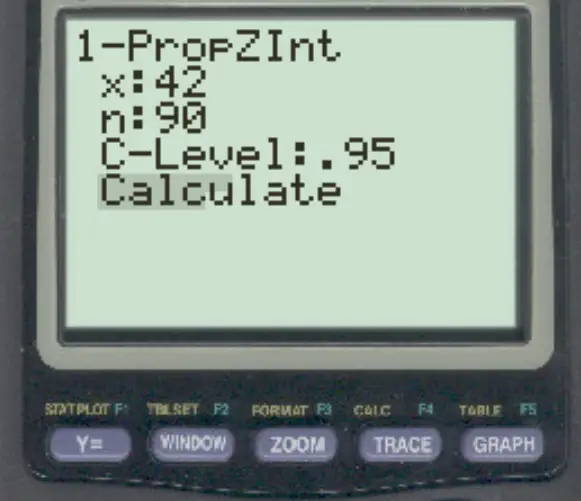
Das Konfidenzintervall beträgt (.3636, .56974) :

Die Fehlerspanne würde der halben Breite dieses Konfidenzintervalls entsprechen, d. h.:

Fehlergrenze: (.56974 – .3636) / 2 = .10307

Zusätzliche Ressourcen

So berechnen Sie Konfidenzintervalle auf einem TI-84-Rechner
So finden Sie den kritischen Z-Wert auf einem TI-84-Rechner
So ermitteln Sie den kritischen Wert T auf einem TI-84-Rechner