So berechnen sie die kochdistanz in sas

Die Cook-Distanz wird verwendet, um einflussreiche Beobachtungen in einem Regressionsmodell zu identifizieren.

Die Formel für die Cook-Distanz lautet:

d _i = (r _i ² / p*MSE) * (h _ii / (1-h _ii ) ² )

Gold:

• r _i ist der i ^-te Rest
• p ist die Anzahl der Koeffizienten im Regressionsmodell
• MSE ist der mittlere quadratische Fehler
• h _ii ist der ^i-te Hebelwert

Im Wesentlichen misst die Cook-Distanz, wie stark sich alle angepassten Werte des Modells ändern, wenn die i- ^te Beobachtung entfernt wird.

Je größer der Wert der Cook-Distanz ist, desto einflussreicher ist eine bestimmte Beobachtung.

Im Allgemeinen wird davon ausgegangen, dass jede Beobachtung mit einer Cook-Distanz von mehr als 4/n (wobei n = Gesamtbeobachtungen) einen großen Einfluss hat.

Das folgende Beispiel zeigt, wie die Cook-Distanz für jede Beobachtung in einem Regressionsmodell in SAS berechnet wird.

Beispiel: Berechnung der Kochdistanz in SAS

Nehmen wir an, wir haben den folgenden Datensatz in SAS:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

Wir können PROC REG verwenden, um ein einfaches lineares Regressionsmodell an diesen Datensatz anzupassen, und dann die OUTPUT- Anweisung mit der COOKD- Anweisung verwenden, um die Cook-Distanz für jede Beobachtung im Regressionsmodell zu berechnen:

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

Die Endergebnistabelle zeigt den Originaldatensatz zusammen mit der Cook-Distanz für jede Beobachtung:

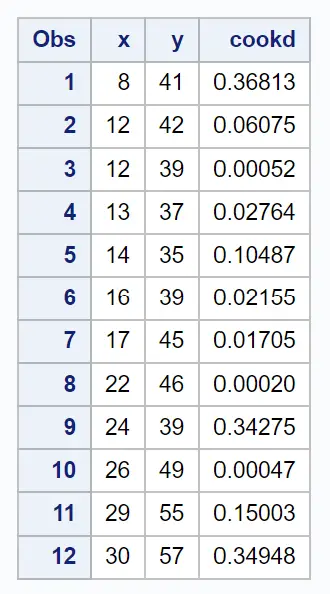
Wir können zum Beispiel sehen:

• Die Cook-Distanz für die erste Beobachtung beträgt 0,36813 .
• Die Cook-Distanz für die zweite Beobachtung beträgt 0,06075 .
• Die Cook-Distanz für die dritte Beobachtung beträgt 0,00052 .

Und so weiter.

Die PROC REG- Prozedur erzeugt außerdem mehrere Diagnosediagramme in der Ausgabe, und das Cook-Distanzdiagramm ist in dieser Ausgabe zu sehen:

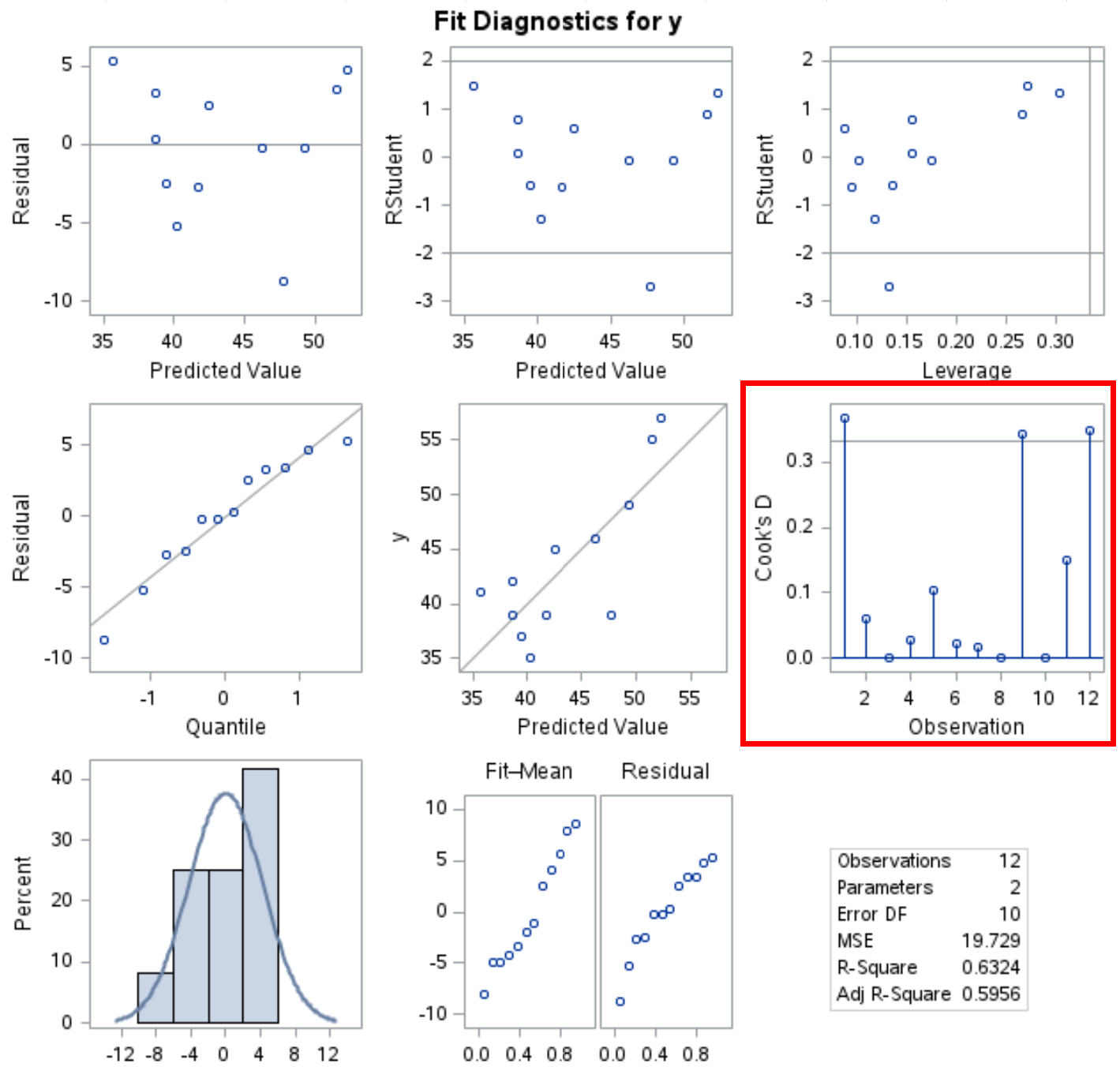
Die x-Achse zeigt die Beobachtungsnummer und die y-Achse zeigt die Cook-Distanz für jede Beobachtung.

Beachten Sie, dass eine Grenzlinie bei 4/n liegt (in diesem Fall n = 12, also liegt die Grenzlinie bei 0,33) und wir sehen können, dass drei Beobachtungen im Datensatz größer als diese Linie sind.

Dies deutet darauf hin, dass diese Beobachtungen einen großen Einfluss auf das Regressionsmodell haben könnten und möglicherweise vor der Interpretation der Modellergebnisse genauer untersucht werden sollten.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So erstellen Sie ein Restdiagramm in SAS
So erstellen Sie Histogramme in SAS
So erstellen Sie Punktwolken in SAS
So identifizieren Sie Ausreißer in SAS