So finden sie z-scores in einem bestimmten bereich (mit beispielen)
Es gibt drei Möglichkeiten, den Z-Score zu ermitteln, der einer bestimmten Fläche unter einer Normalverteilungskurve entspricht
1. Verwenden Sie die Z-Tabelle.
2. Verwenden Sie den Z-Score-Perzentilrechner.
3. Verwenden Sie die Funktion invNorm() auf einem TI-84-Rechner .
Die folgenden Beispiele zeigen, wie Sie mit jeder dieser Methoden den Z-Score ermitteln, der einer bestimmten Fläche unter einer Normalverteilungskurve entspricht.
Beispiel 1: Suchen Sie links den angegebenen Bereich des Z-Scores
Suchen Sie links den Z-Score, der 15,62 % des Verbreitungsgebiets darstellt.
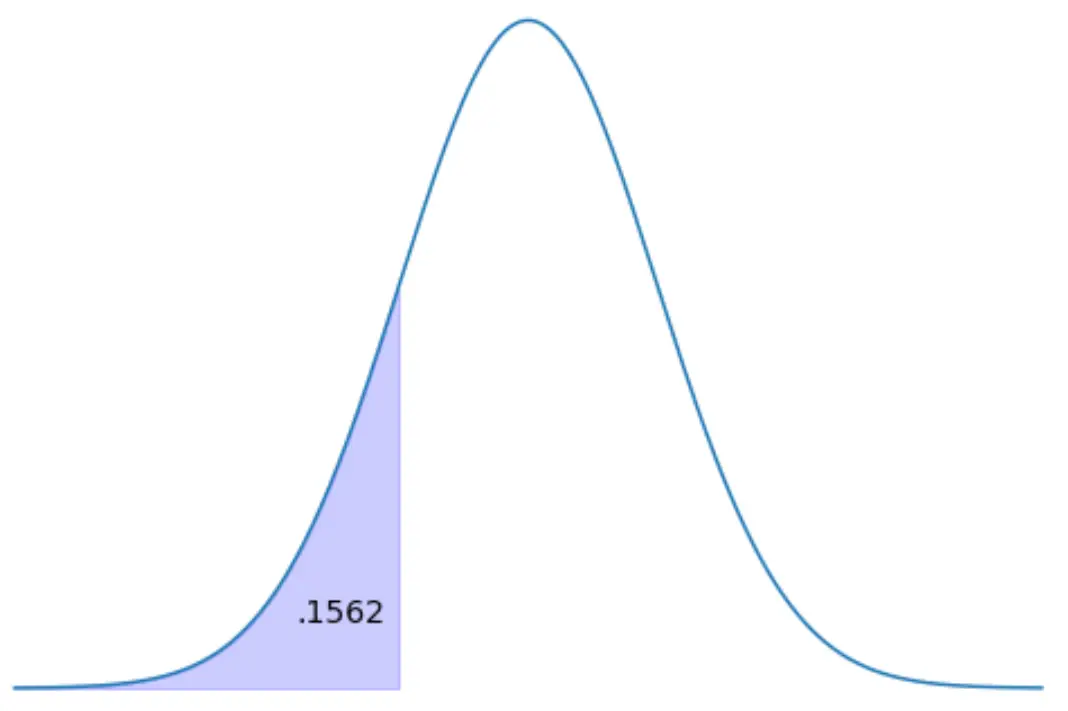
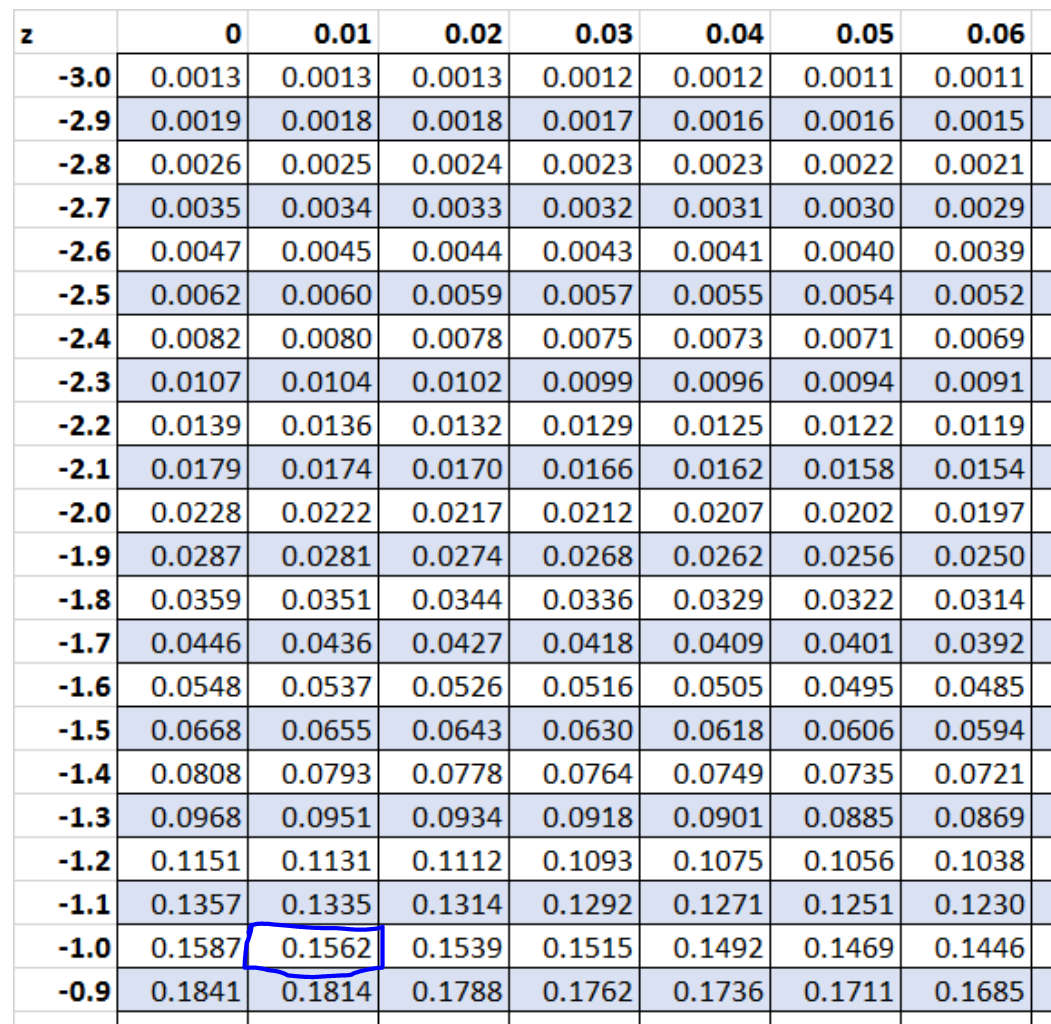
Methode 1: Verwenden Sie die Z-Tabelle.
Der Z-Score, der einem Wert von 0,1562 in der Z-Tabelle entspricht, ist -1,01 .
2. Verwenden Sie den Z-Score-Perzentilrechner.
Laut dem Z-Score-Perzentilrechner beträgt der Z-Score, der einem Perzentil von 0,1562 entspricht, -1,01 .
3. Verwenden Sie die Funktion invNorm() auf einem TI-84-Rechner.
Bei Verwendung der Funktion invNorm() auf einem TI-84-Rechner beträgt der Z-Score, der einer Fläche von 0,1562 auf der linken Seite entspricht, -1,01 .
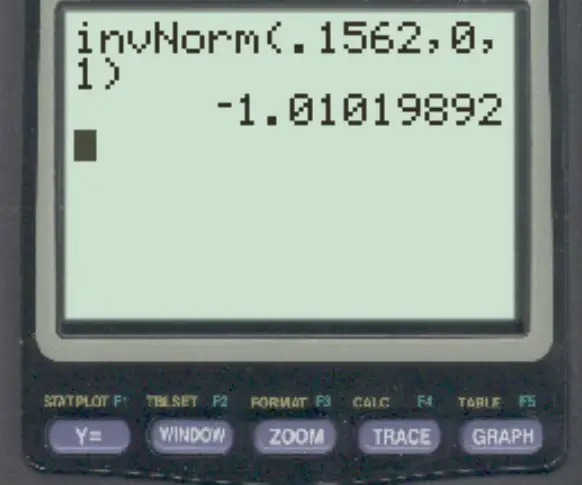
Beachten Sie, dass alle drei Methoden zum gleichen Ergebnis führen.
Beispiel 2: Suchen Sie rechts den angegebenen Bereich des Z-Scores
Suchen Sie rechts den Z-Score, der 37,83 % des Verbreitungsgebiets darstellt.
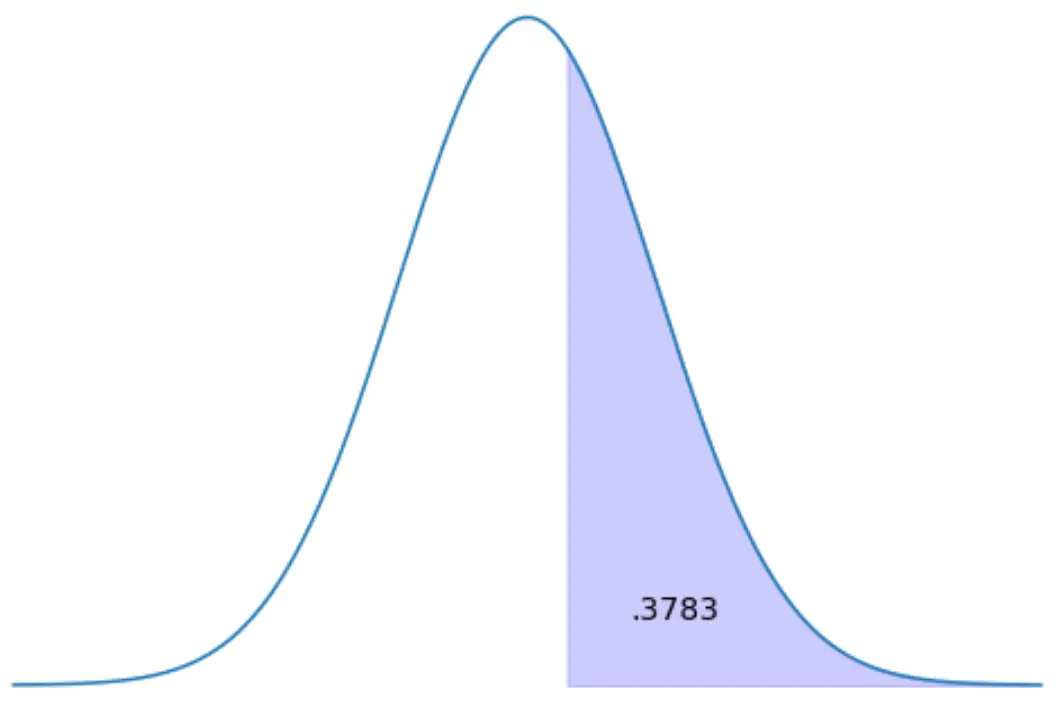
Methode 1: Verwenden Sie die Z-Tabelle.
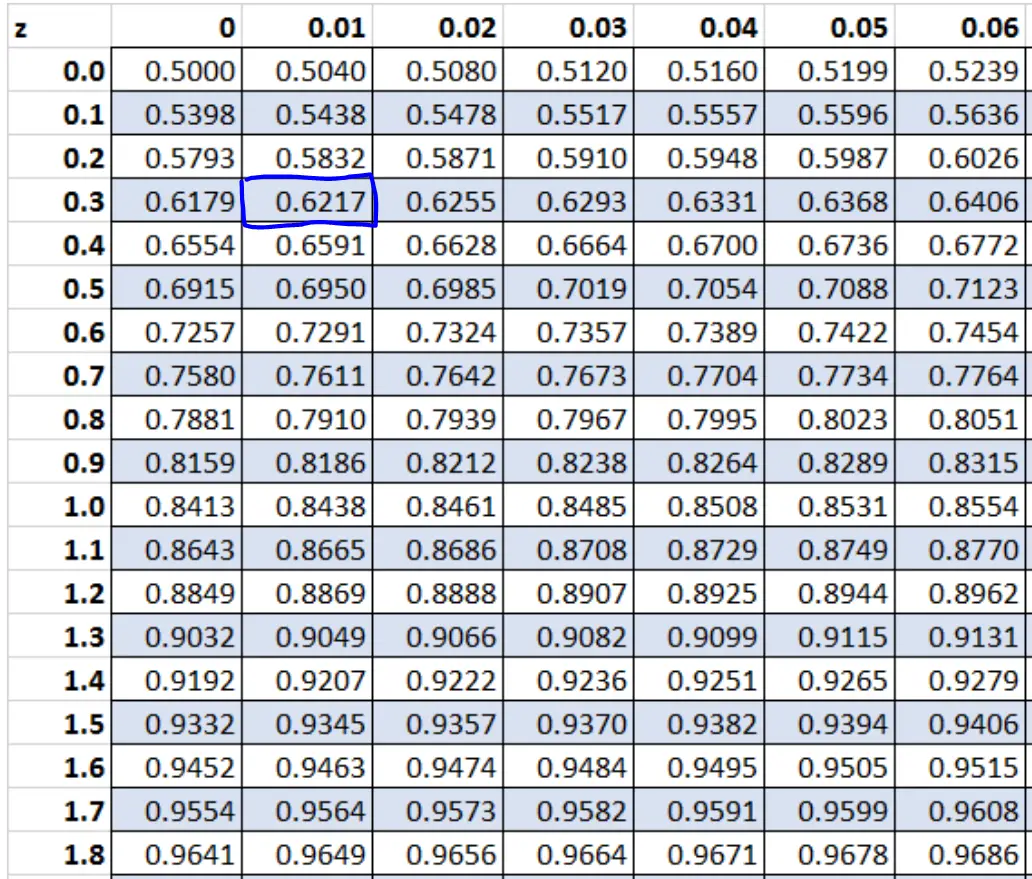
Das Z-Diagramm zeigt den Bereich links von den verschiedenen Z-Werten. Wenn wir also wissen, dass die Fläche rechts 0,3783 beträgt, dann beträgt die Fläche links 1 – 0,3783 = 0,6217.
Der Z-Score, der in der Z-Tabelle einem Wert von 0,6217 entspricht, beträgt 0,31.
2. Verwenden Sie den Z-Score-Perzentilrechner.
Laut dem Z-Score-Perzentilrechner beträgt der Z-Score, der einem Perzentil von 0,6217 entspricht, . 3099 .
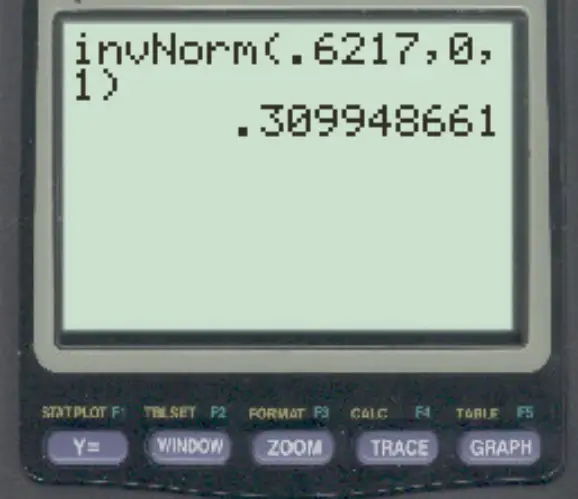
3. Verwenden Sie die Funktion invNorm() auf einem TI-84-Rechner.
Bei Verwendung der Funktion invNorm() auf einem TI-84-Rechner beträgt der Z-Score, der einem Bereich von .6217 auf der linken Seite entspricht, .3099 .
Beispiel 3: Finden von Z-Scores im Bereich zwischen zwei Werten
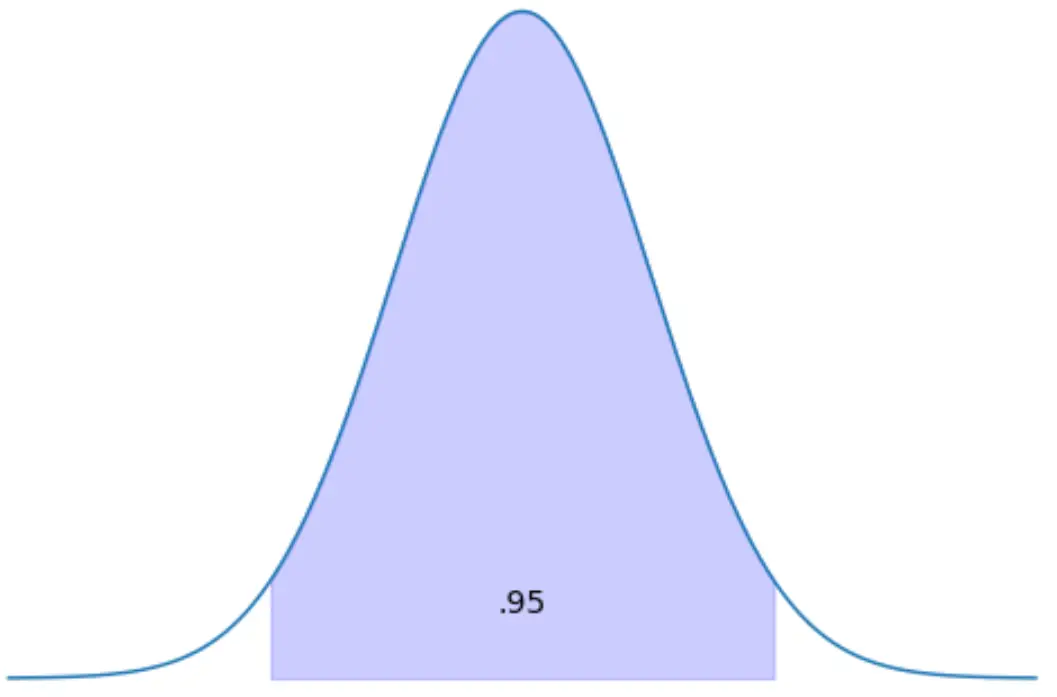
Finden Sie die Z-Scores, zwischen denen 95 % des Verteilungsbereichs liegen.
Methode 1: Verwenden Sie die Z-Tabelle.
Wenn 95 % der Verteilung zwischen zwei Z-Scores liegen, bedeutet das, dass 5 % der Verteilung außerhalb der Z-Scores liegen.
2,5 % der Verteilung sind also niedriger als einer der Z-Scores und 2,5 % der Verteilung sind höher als der andere Z-Score.
Wir können also 0,025 in der Z-Tabelle nachschlagen. Der Z-Score, der 0,025 in der Z-Tabelle entspricht, ist -1,96 .
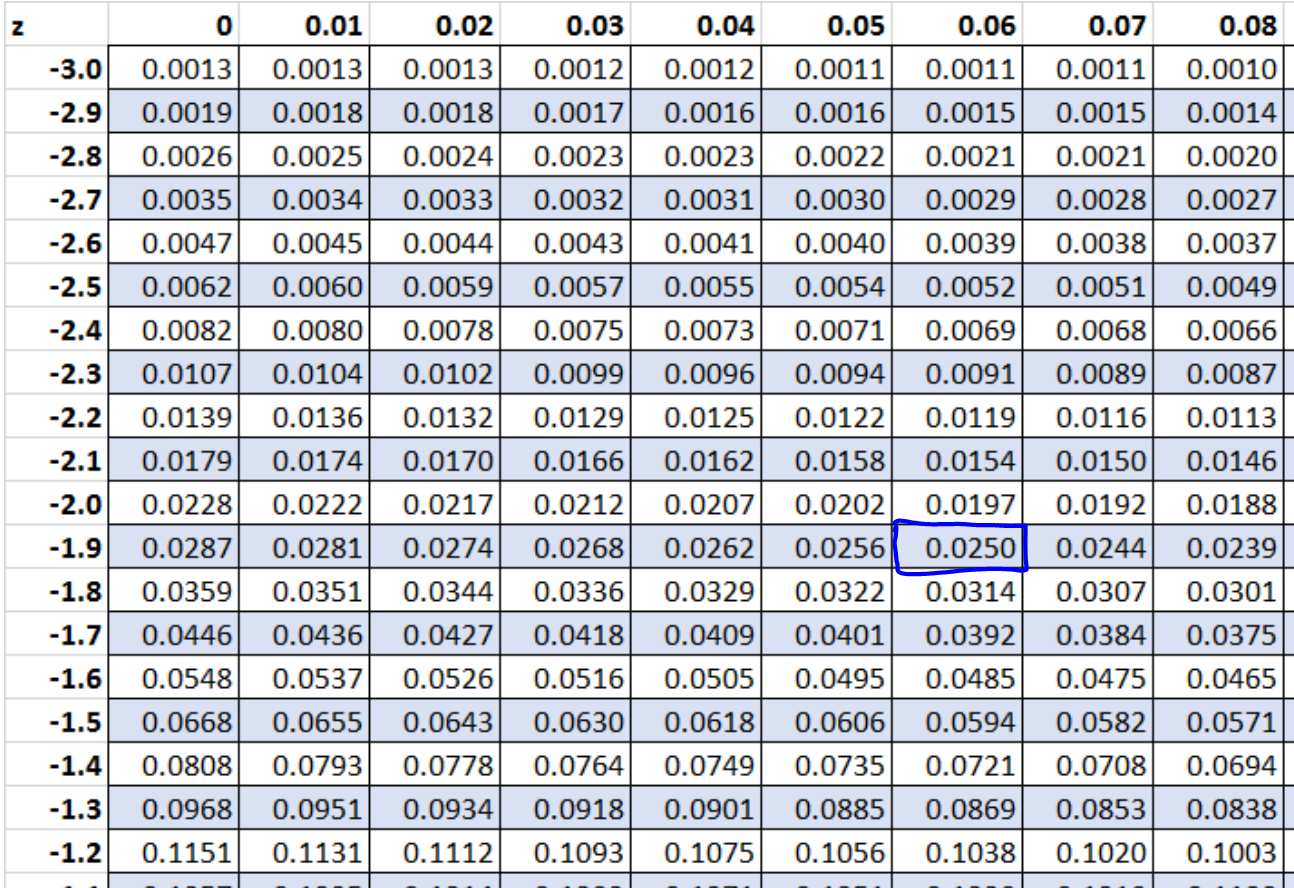
Die Z-Scores, die 95 % der Verteilung zwischen ihnen enthalten, sind also -1,96 und 1,96 .
2. Verwenden Sie den Z-Score-Perzentilrechner.
Laut dem Z-Score-Perzentilrechner beträgt der Z-Score, der einem Perzentil von 0,025 entspricht, -1,96 .
Die Z-Scores, die 95 % der Verteilung zwischen ihnen enthalten, sind also -1,96 und 1,96 .
3. Verwenden Sie die Funktion invNorm() auf einem TI-84-Rechner.
Bei Verwendung der Funktion invNorm() auf einem TI-84-Rechner beträgt der Z-Score, der einer Fläche von 0,025 nach links entspricht, -1,96 .
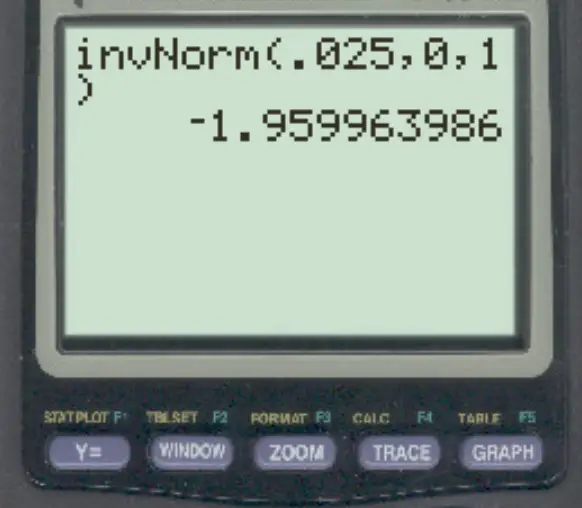
Die Z-Scores, die 95 % der Verteilung zwischen ihnen enthalten, sind also -1,96 und 1,96 .
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen