So finden sie die lineare regressionsgleichung aus einer tabelle

Häufig möchten Sie möglicherweise eine lineare Regressionsgleichung aus einer Datentabelle finden.

Angenommen, Sie erhalten die folgende Datentabelle:

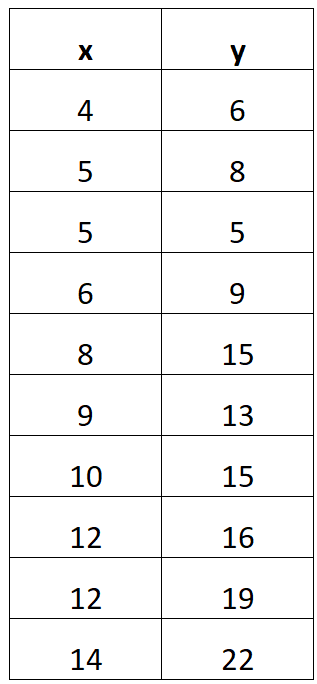
Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie aus dieser Datentabelle eine lineare Regressionsgleichung finden.

Schritt 1: Berechnen Sie X*Y, X ² und Y ²

Zunächst berechnen wir die folgenden Metriken für jede Zeile:

• x*y
• ^x2
• und ²

Der folgende Screenshot zeigt, wie das geht:

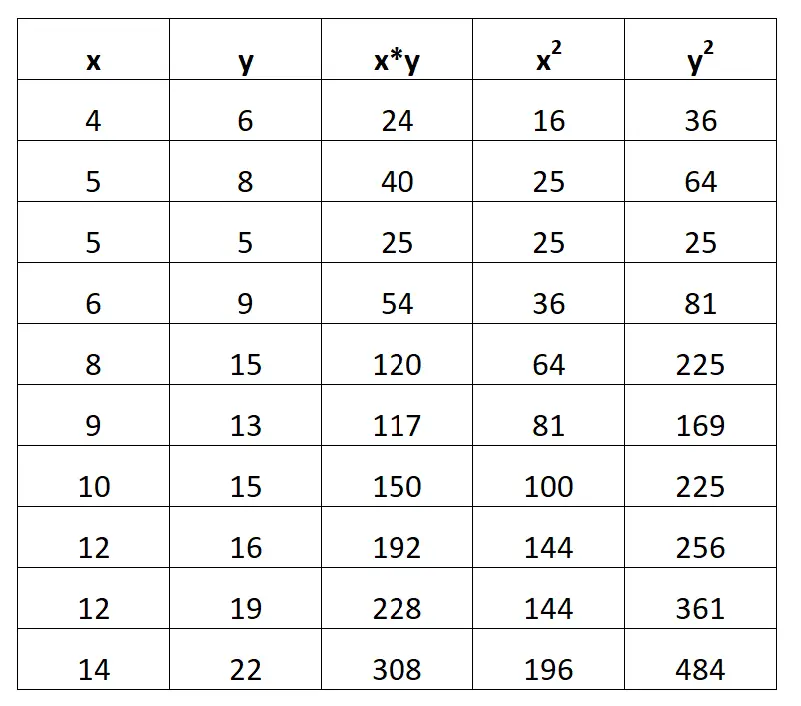
Schritt 2: Berechnen Sie ΣX, ΣY, ΣX*Y, ΣX ² und ΣY ²

Als nächstes berechnen wir die Summe jeder Spalte:

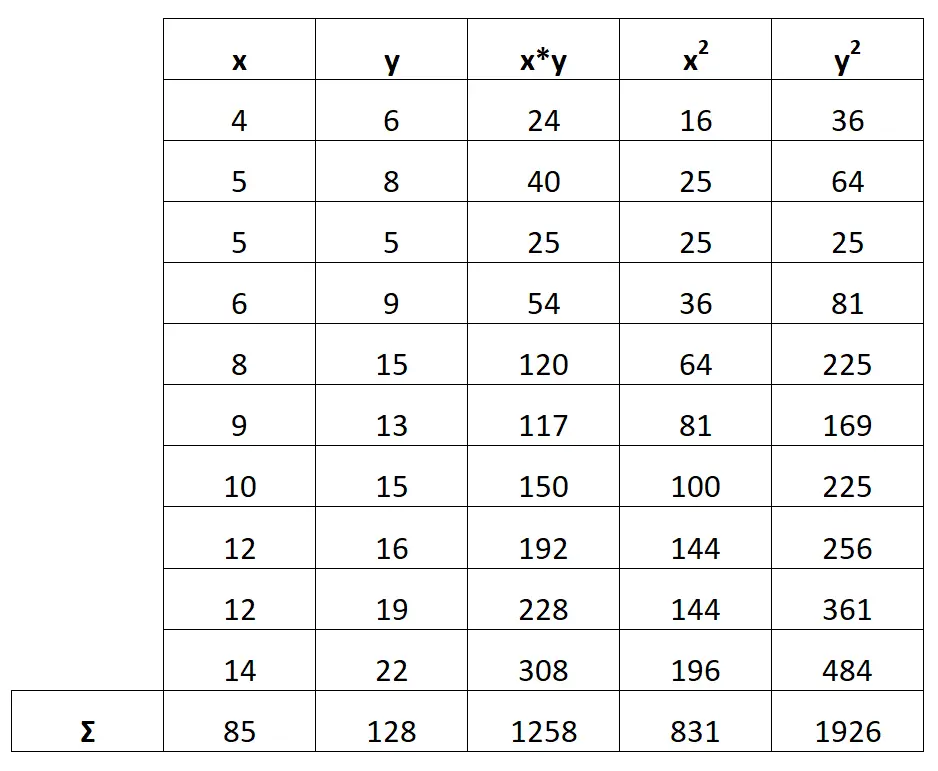
Schritt 3: Berechnen Sie b ₀

Die Formel zur Berechnung des Achsenabschnitts der Regressionsgleichung, b ₀ , lautet:

• b ₀ = ((Σy)(Σx ² ) – (Σx)(Σxy)) / (n(Σx ² ) – (Σx) ² )
• b ₀ = ((128)(831) – (85)(1258)) / (10(831) – (85) ² )
• _b0 = -0,518

Hinweis : In der Formel stellt n die Gesamtzahl der Beobachtungen dar. In diesem Beispiel gab es insgesamt 10 Beobachtungen.

Schritt 4: Berechnen Sie b ₁

Die Formel zur Berechnung der Steigung der Regressionsgleichung, b ₁ , lautet:

• b ₁ = (n(Σxy) – (Σx)(Σy)) / (n(Σx ² ) – (Σx) ² )
• b ₁ = (10(1258) – (85)(128)) / (10(831) – (85) ² )
• _b1 = 1,5668

Schritt 5: Schreiben Sie die lineare Regressionsgleichung

Die endgültige lineare Regressionsgleichung kann wie folgt geschrieben werden:

• ŷ = b ₀ + b ₁ x

Unsere lineare Regressionsgleichung würde also wie folgt geschrieben werden:

• ŷ = -0,518 + 1,5668x

Wir können überprüfen, ob diese Antwort richtig ist, indem wir die Werte aus der Tabelle in den einfachen linearen Regressionsrechner eingeben:

Wir können sehen, dass die lineare Regressionsgleichung des Rechners mit der von uns manuell berechneten übereinstimmt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur linearen Regression:

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
So interpretieren Sie Regressionskoeffizienten