So ermitteln sie die wahrscheinlichkeit anhand eines z-scores: mit beispielen

Der einfachste Weg, die Wahrscheinlichkeit aus einem Z-Score zu ermitteln, besteht darin, einfach die Wahrscheinlichkeit zu ermitteln, die dem Z-Score in der Z-Tabelle entspricht.

In diesem Tutorial wird erklärt, wie Sie mithilfe der Z-Tabelle die folgenden Wahrscheinlichkeiten ermitteln:

• Die Wahrscheinlichkeit, dass ein Wert unter einem bestimmten Z-Score liegt.
• Die Wahrscheinlichkeit, dass ein Wert größer als ein bestimmter Z-Score ist.
• Die Wahrscheinlichkeit, dass ein Wert zwischen zwei bestimmten Z-Scores liegt.

Lass uns gehen!

Beispiel 1: Wahrscheinlichkeit kleiner als ein bestimmter Z-Score

Angenommen, wir möchten die Wahrscheinlichkeit ermitteln, dass ein Wert in einer bestimmten Verteilung einen Z-Score von weniger als z = 0,25 hat.

Um diese Wahrscheinlichkeit zu finden, müssen wir in der Z-Tabelle nach 0,25 suchen:

Die Wahrscheinlichkeit, dass ein Wert in einer bestimmten Verteilung einen Z-Score von weniger als z = 0,25 hat, beträgt ungefähr 0,5987 .

Hinweis : In Prozent könnte dieser Wert auch als 59,87 % angegeben werden.

Beispiel 2: Wahrscheinlichkeit größer als ein bestimmter Z-Score

Angenommen, wir möchten die Wahrscheinlichkeit ermitteln, dass ein Wert in einer bestimmten Verteilung einen Z-Score größer als z = -0,5 hat.

Um diese Wahrscheinlichkeit zu finden, müssen wir in der z-Tabelle nach -0,5 suchen:

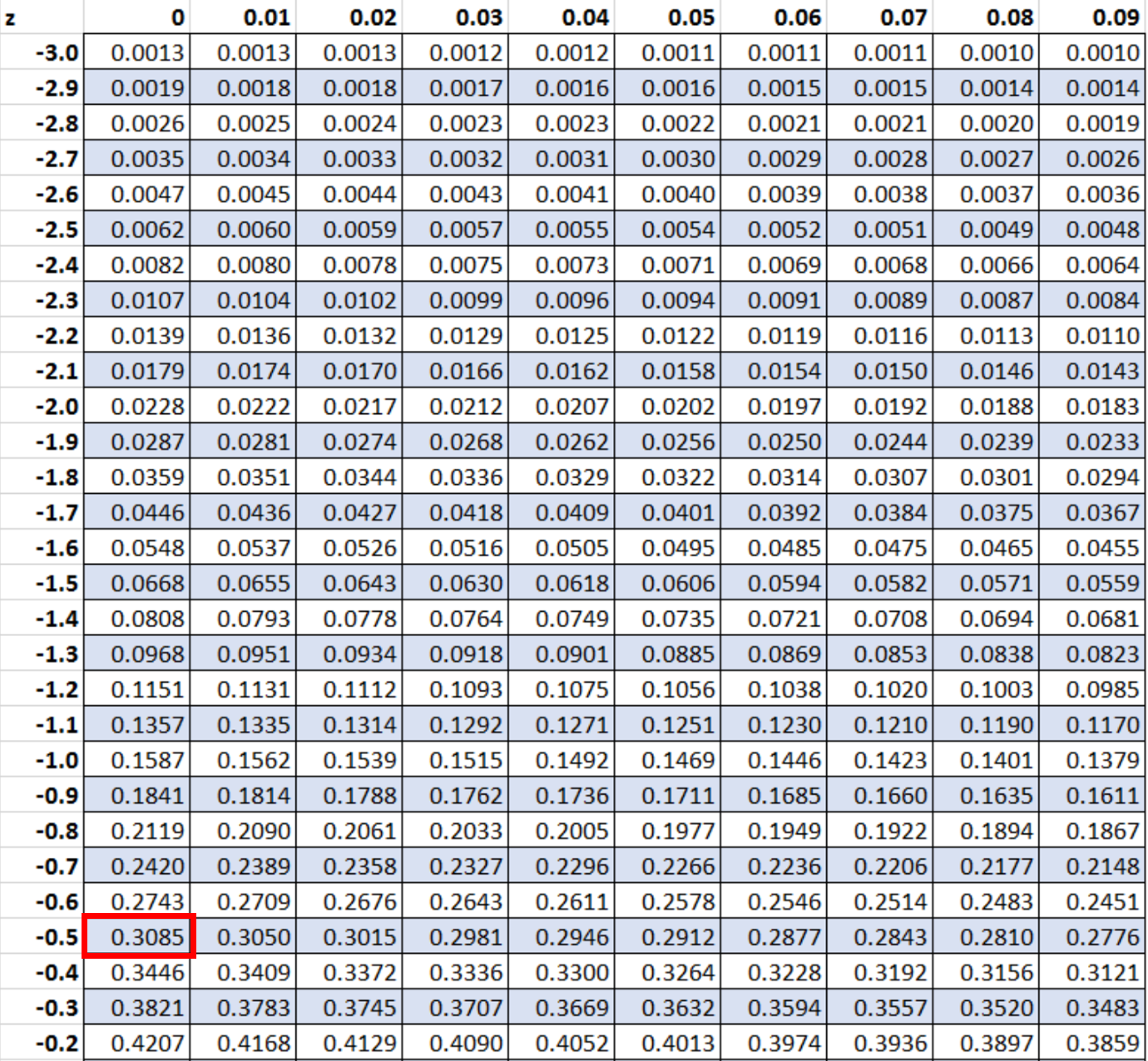
Die Wahrscheinlichkeit, die einem Z-Score von -0,5 entspricht, beträgt 0,3085.

Da wir jedoch die Wahrscheinlichkeit wissen möchten, dass ein Wert in einer bestimmten Verteilung einen Z-Score größer als -0,5 hat, müssen wir diese Wahrscheinlichkeit von 1 subtrahieren.

Die Wahrscheinlichkeit, dass ein Wert in einer bestimmten Verteilung einen Z-Score größer als -0,5 hat, beträgt also: 1 – 0,3085 = 0,6915 .

Beispiel 3: Wahrscheinlichkeit zwischen zwei Z-Scores

Angenommen, wir möchten die Wahrscheinlichkeit ermitteln, dass ein Wert in einer bestimmten Verteilung einen Z-Score zwischen z = 0,4 und z = 1 hat.

Zuerst suchen wir nach dem Wert 0,4   in Tabelle z:

Als nächstes suchen wir nach dem Wert 1   in Tabelle z:

Als nächstes subtrahieren wir den kleineren Wert vom größeren Wert: 0,8413 – 0,6554 = 0,1859 .

Die Wahrscheinlichkeit, dass ein Wert in einer gegebenen Verteilung einen Z-Score zwischen z = 0,4 und z = 1 hat, beträgt also ungefähr 0,1859 .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Z-Scores:

5 Beispiele für die Verwendung von Z-Scores im wirklichen Leben
So konvertieren Sie Z-Scores in Roh-Scores
So finden Sie Z-Werte in einem bestimmten Bereich