Poisson-verteilung oder normalverteilung: was ist der unterschied?

Die Poisson-Verteilung und die Normalverteilung sind zwei der am häufigsten verwendeten Wahrscheinlichkeitsverteilungen in der Statistik.

Dieses Tutorial bietet eine kurze Erklärung jeder Distribution sowie zwei wichtige Unterschiede zwischen den Distributionen.

Ein Überblick: die Poisson-Verteilung

Die Poisson-Verteilung beschreibt die Wahrscheinlichkeit, in einem bestimmten Zeitintervall k Erfolge zu erzielen.

Wenn eine Zufallsvariable X einer Poisson-Verteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = λ ^k * e ^{– λ} / k!

Gold:

• λ: durchschnittliche Anzahl von Erfolgen, die während eines bestimmten Intervalls auftreten
• k: Anzahl der Erfolge
• e: eine Konstante, die ungefähr 2,71828 entspricht

Angenommen, in einem bestimmten Krankenhaus gibt es durchschnittlich zwei Geburten pro Stunde. Mit der obigen Formel können wir die Wahrscheinlichkeit ermitteln, in einer bestimmten Stunde drei Geburten zu erleben:

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Die Wahrscheinlichkeit, in einer Stunde drei Geburten zu erleben, beträgt 0,1805 .

Ein Überblick: die Normalverteilung

Die Normalverteilung beschreibt die Wahrscheinlichkeit, dass eine Zufallsvariable in einem bestimmten Intervall einen Wert annimmt.

Die Wahrscheinlichkeitsdichtefunktion einer Normalverteilung kann wie folgt geschrieben werden:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

Gold:

• σ: Standardabweichung der Verteilung
• μ: Mittelwert der Verteilung
• x: Wert der Zufallsvariablen

Angenommen, das Gewicht einer bestimmten Otterart ist normal verteilt mit μ = 40 Pfund und σ = 5 Pfund.

Wenn wir aus dieser Population zufällig einen Otter auswählen, können wir die folgende Formel verwenden, um die Wahrscheinlichkeit zu ermitteln, dass er zwischen 38 und 42 Pfund wiegt:

P ( ^{38 < /5) 2} = 0,3108

Die Wahrscheinlichkeit, dass der zufällig ausgewählte Otter zwischen 38 und 42 Pfund wiegt, beträgt 0,3108 .

Unterschied Nr. 1: Diskret vs. Kontinuierliche Daten

Der erste Unterschied zwischen der Poisson-Verteilung und der Normalverteilung besteht in der Art der Daten, die von jeder Wahrscheinlichkeitsverteilung modelliert werden.

Eine Poisson-Verteilung wird verwendet, wenn mit diskreten Daten gearbeitet wird, die nur ganzzahlige Werte gleich oder größer Null annehmen können. Hier sind einige Beispiele:

• Anzahl der pro Stunde eingegangenen Anrufe in einem Callcenter
• Anzahl der Kunden pro Tag in einem Restaurant
• Anzahl der Autounfälle pro Monat

In jedem Szenario kann die Zufallsvariable nur den Wert 0, 1, 2, 3 usw. annehmen.

Bei der Arbeit mit kontinuierlichen Daten wird eine Normalverteilung verwendet, die jeden Wert von negativ unendlich bis positiv unendlich annehmen kann. Hier sind einige Beispiele:

• Gewicht eines bestimmten Tieres
• Höhe einer bestimmten Pflanze
• Marathonzeiten der Frauen
• Temperatur in Celsius

In diesen Szenarien können Zufallsvariablen jeden Wert wie -11,3, 21,343435, 85 usw. annehmen.

Unterschied Nr. 2: Form der Verteilungen

Der zweite Unterschied zwischen der Poisson-Verteilung und der Normalverteilung liegt in der Form der Verteilungen.

Eine Normalverteilung hat immer eine Glockenform:

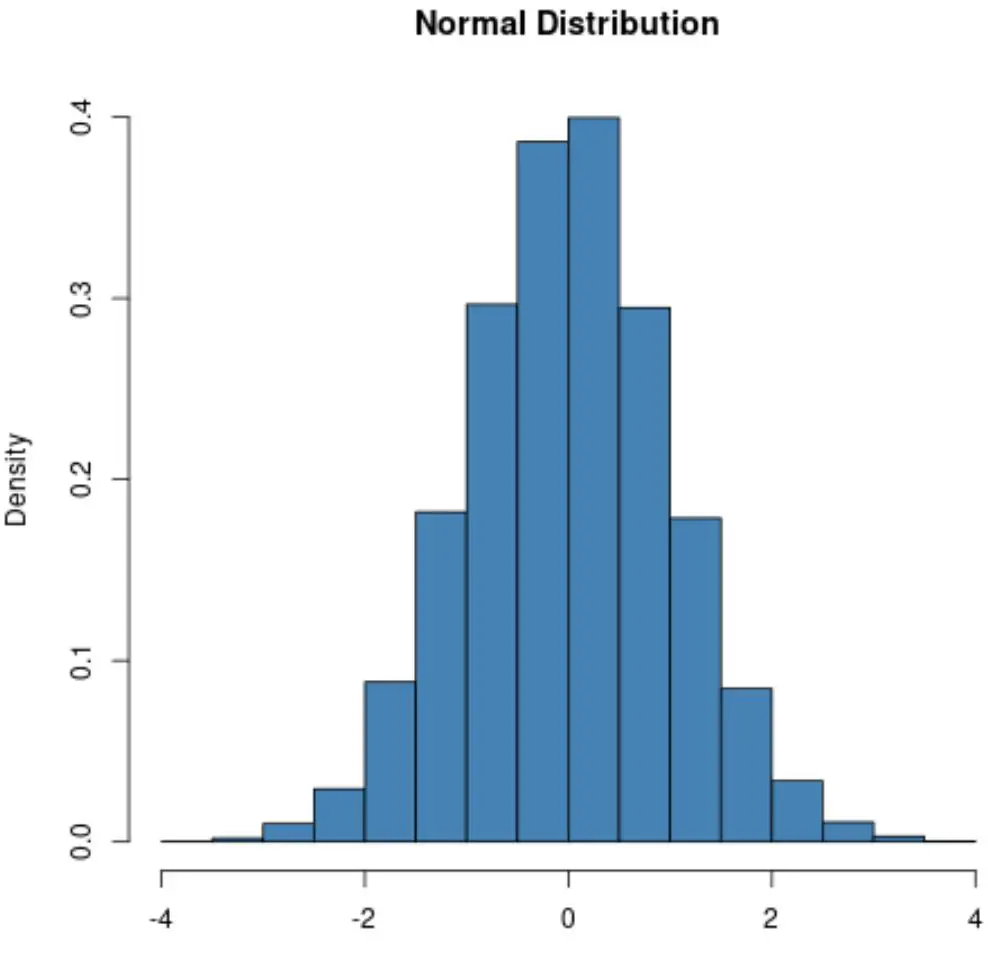
Allerdings variiert die Form der Poisson-Verteilung je nach Mittelwert der Verteilung.

Beispielsweise ist eine Poisson-Verteilung mit einem kleinen Mittelwert wie μ = 3 stark rechtsschief :

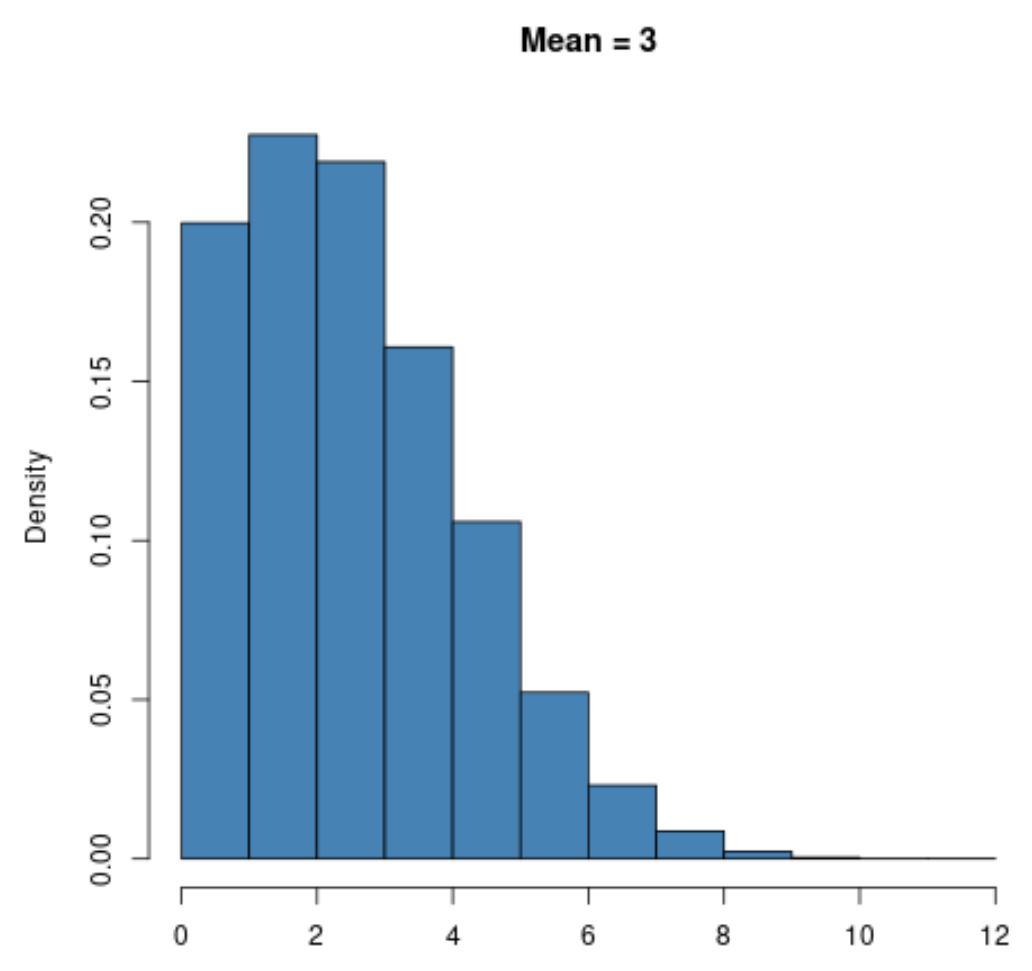
Eine Poisson-Verteilung mit einem größeren Mittelwert wie μ = 20 weist jedoch genau wie die Normalverteilung eine Glockenform auf:

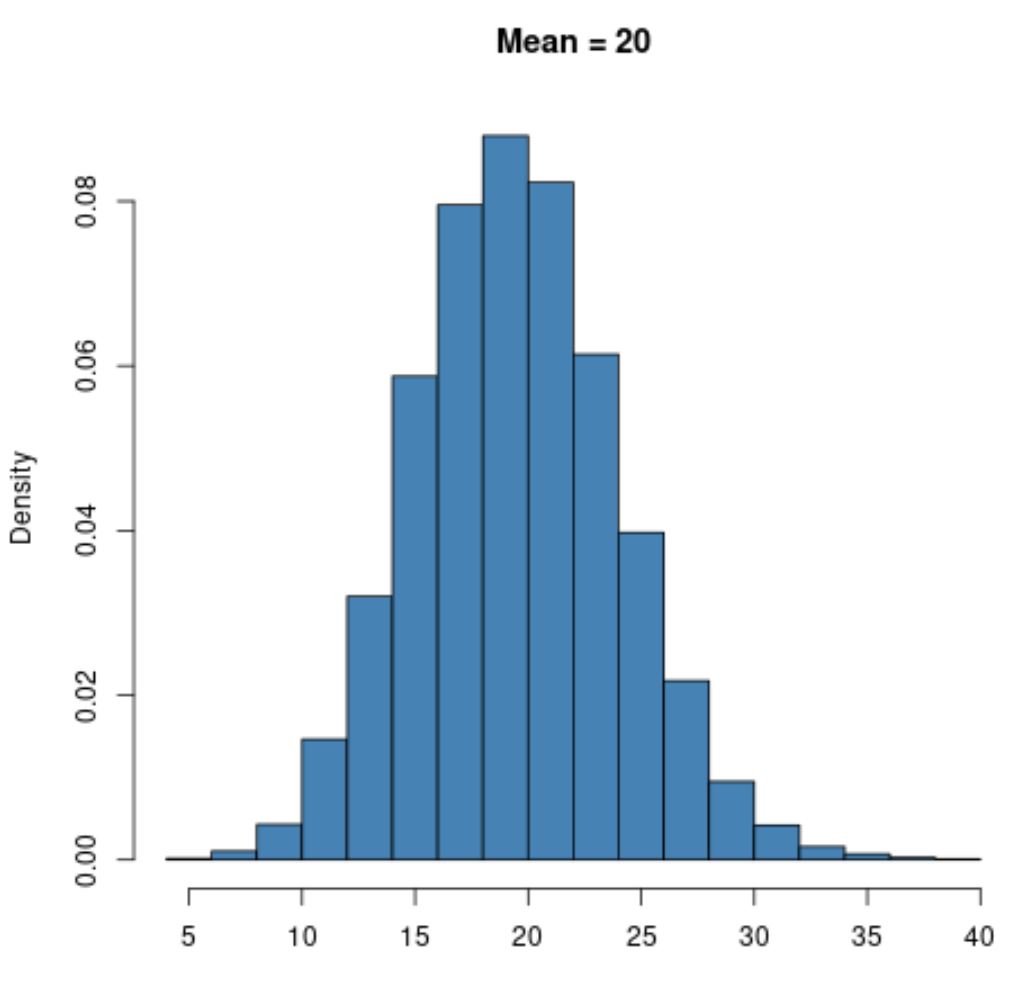
Beachten Sie, dass die untere Grenze einer Poisson-Verteilung unabhängig vom Mittelwert immer Null ist, da eine Poisson-Verteilung nur mit ganzzahligen Werten gleich oder größer als Null verwendet werden kann.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Poisson-Verteilung:

Eine Einführung in die Poisson-Verteilung
Die vier Hypothesen der Poisson-Verteilung
5 konkrete Beispiele der Poisson-Verteilung

Die folgenden Tutorials bieten zusätzliche Informationen zur Normalverteilung:

Eine Einführung in die Normalverteilung
6 konkrete Beispiele der Normalverteilung
Normalverteilungs-Datensatzgenerator