So zeichnen sie eine poisson-verteilung in r auf

Um die Wahrscheinlichkeitsmassenfunktion für einePoisson-Verteilung in R darzustellen, können wir die folgenden Funktionen verwenden:

• dpois(x, lambda) , um die Wahrscheinlichkeitsmassenfunktion zu erstellen
• plot(x, y, type = ‚h‘) , um die Wahrscheinlichkeitsmassenfunktion darzustellen, wobei angegeben wird, dass es sich bei der Darstellung um ein Histogramm handelt (type=’h‘)

Um die Wahrscheinlichkeitsmassenfunktion darzustellen, geben Sie einfach Lambda an   (zum Beispiel die Häufigkeit von Ereignissen) in der Funktion dpois() .

Der folgende Code veranschaulicht beispielsweise, wie eine Wahrscheinlichkeitsmassenfunktion für eine Poisson-Verteilung mit Lambda = 5 dargestellt wird:

 #define range of "successes"
success <- 0:20

#create plot of probability mass function
plot(success, dois(success, lambda=5), type='h')

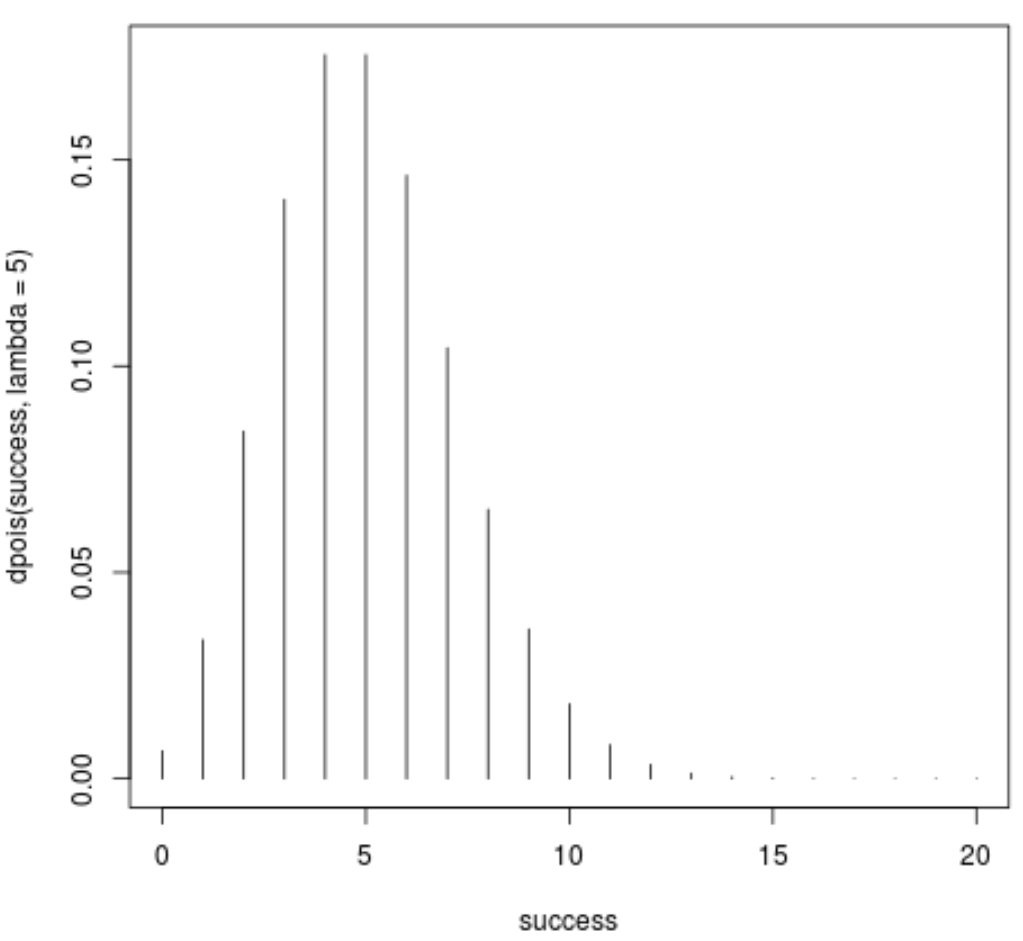
Die x-Achse zeigt die Anzahl der „Erfolge“ – zum Beispiel die Anzahl der aufgetretenen Ereignisse – und die y-Achse zeigt die Wahrscheinlichkeit, diese Anzahl an Erfolgen in 20 Versuchen zu erreichen.

Wir können einen Titel hinzufügen, die Achsenbeschriftungen ändern und die Breite der Linien erhöhen, um die Handlung ästhetisch ansprechender zu gestalten:

 success <- 0:20

plot(success, dois(success, lambda=5),
     type='h',
     main='Fish Distribution (lambda = 5)',
     ylab='Probability',
     xlab ='# Successes',
     lwd=3)

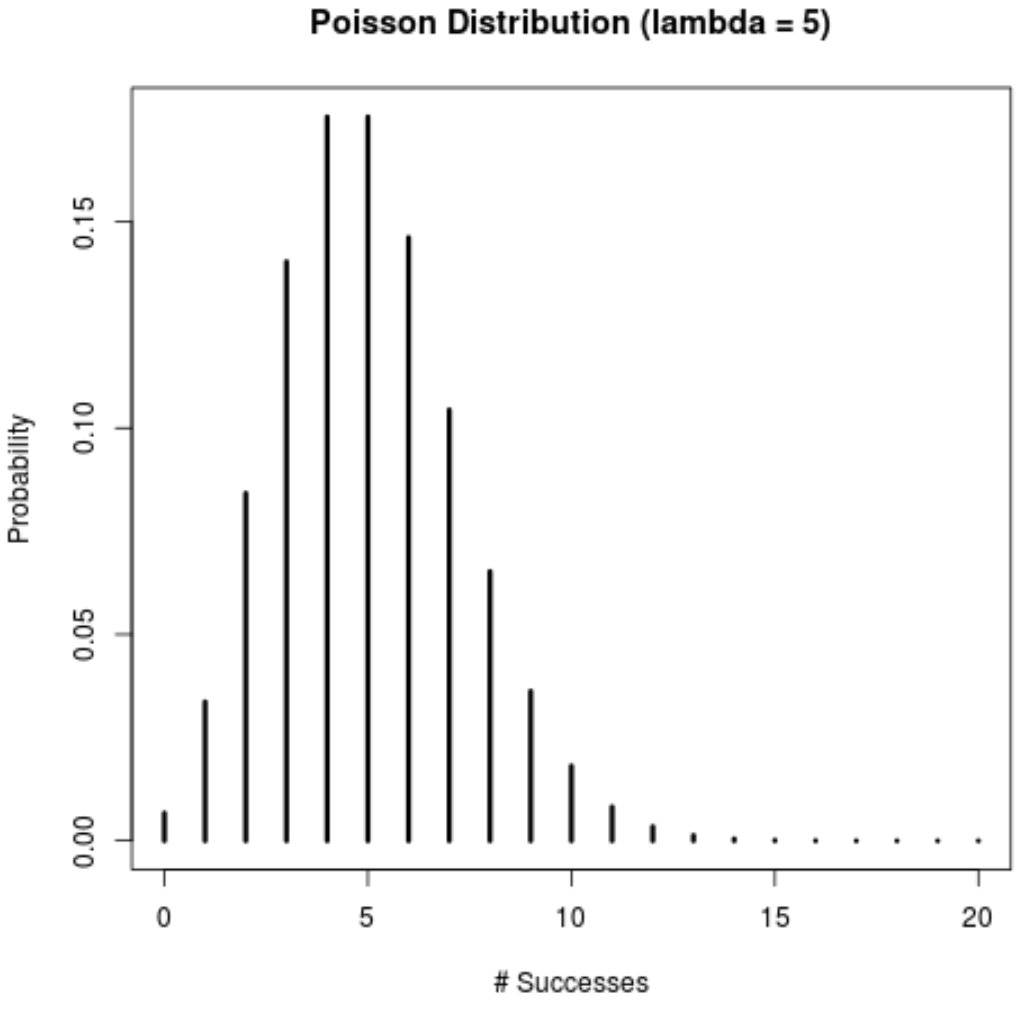
Wir können den folgenden Code verwenden, um die tatsächlichen Wahrscheinlichkeiten für jede im Diagramm angezeigte Anzahl von Erfolgen zu ermitteln:

 #prevent R from displaying numbers in scientific notation
options(scipen=999) 

#define range of successes
success <- 0:20

#display probability of success for each number of trials
dpois(success, lambda=5)

[1] 0.0067379469991 0.0336897349954 0.0842243374886 0.1403738958143
[5] 0.1754673697679 0.1754673697679 0.1462228081399 0.1044448629571
[9] 0.0652780393482 0.0362655774156 0.0181327887078 0.0082421766854
[13] 0.0034342402856 0.0013208616483 0.0004717363030 0.0001572454343
[17] 0.0000491391982 0.0000144527054 0.0000040146404 0.0000010564843
[21] 0.0000002641211