So verwenden sie die poisson-verteilung in python

Die Poisson-Verteilung beschreibt die Wahrscheinlichkeit, in einem bestimmten Zeitintervall k Erfolge zu erzielen.

Wenn eine Zufallsvariable X einer Poisson-Verteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = λ ^k * e ^{– λ} / k!

Gold:

• λ: durchschnittliche Anzahl von Erfolgen, die während eines bestimmten Intervalls auftreten
• k: Anzahl der Erfolge
• e: eine Konstante, die ungefähr 2,71828 entspricht

In diesem Tutorial wird erklärt, wie Sie die Poisson-Verteilung in Python verwenden.

So erstellen Sie eine Poisson-Verteilung

Mit der Funktion Poisson.rvs(mu, size) können Sie Zufallswerte aus einer Poisson-Verteilung mit einem bestimmten Mittelwert und einer bestimmten Stichprobengröße generieren:

 from scipy. stats import fish

#generate random values from Poisson distribution with mean=3 and sample size=10
fish. rvs (mu=3, size=10)

array([2, 2, 2, 0, 7, 2, 1, 2, 5, 5])

So berechnen Sie Wahrscheinlichkeiten mithilfe einer Poisson-Verteilung

Sie können die Funktionen Poisson.pmf(k, mu) und Poisson.cdf(k, mu) verwenden, um Wahrscheinlichkeiten im Zusammenhang mit der Poisson-Verteilung zu berechnen.

Beispiel 1: Wahrscheinlichkeit gleich einem bestimmten Wert

Ein Geschäft verkauft durchschnittlich 3 Äpfel pro Tag. Wie hoch ist die Wahrscheinlichkeit, dass sie an einem bestimmten Tag 5 Äpfel verkaufen?

 from scipy. stats import fish

#calculate probability
fish. pmf (k=5, mu=3)

0.100819

Die Wahrscheinlichkeit, dass das Geschäft an einem bestimmten Tag 5 Äpfel verkauft, beträgt 0,100819 .

Beispiel 2: Wahrscheinlichkeit kleiner als ein bestimmter Wert

Ein bestimmtes Geschäft verkauft durchschnittlich sieben Fußbälle pro Tag. Wie hoch ist die Wahrscheinlichkeit, dass dieses Geschäft an einem bestimmten Tag vier oder weniger Fußbälle verkauft?

 from scipy. stats import fish

#calculate probability
fish. cdf (k=4, mu=7)

0.172992

Die Wahrscheinlichkeit, dass das Geschäft an einem bestimmten Tag vier oder weniger Fußbälle verkauft, beträgt 0,172992 .

Beispiel 3: Wahrscheinlichkeit größer als ein bestimmter Wert

Ein bestimmter Laden verkauft durchschnittlich 15 Dosen Thunfisch pro Tag. Wie groß ist die Wahrscheinlichkeit, dass dieser Laden an einem bestimmten Tag mehr als 20 Dosen Thunfisch verkauft?

 from scipy. stats import fish

#calculate probability
1-fish. cdf (k=20, mu=15)

0.082971

Die Wahrscheinlichkeit, dass das Geschäft an einem bestimmten Tag mehr als 20 Dosen Thunfisch verkauft, beträgt 0,082971 .

So zeichnen Sie eine Poisson-Verteilung auf

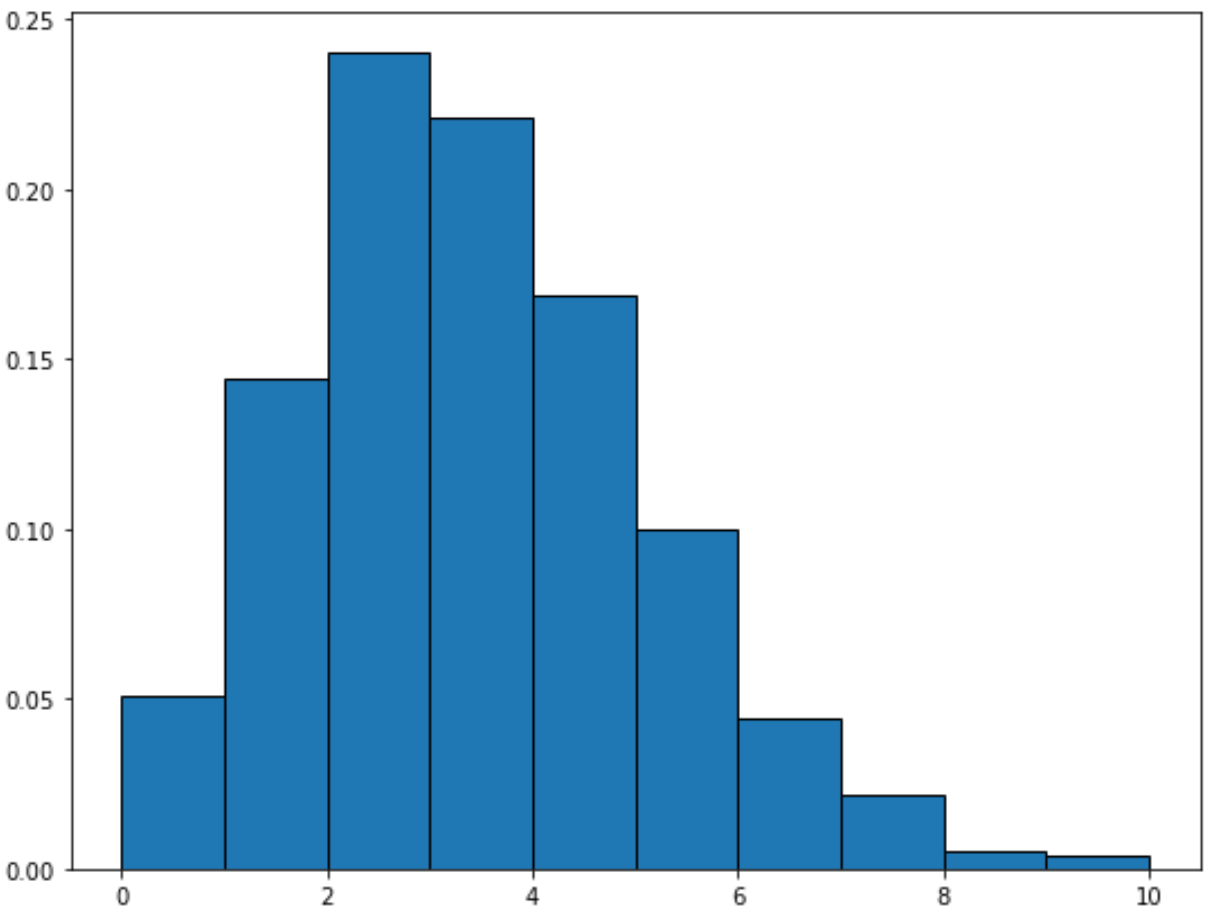
Sie können die folgende Syntax verwenden, um eine Poisson-Verteilung mit einem bestimmten Mittelwert darzustellen:

 from scipy. stats import fish
import matplotlib. pyplot as plt

#generate Poisson distribution with sample size 10000
x = fish. rvs (mu=3, size=10000)

#create plot of Poisson distribution
plt. hist (x, density= True , edgecolor=' black ')

Zusätzliche Ressourcen

Eine Einführung in die Poisson-Verteilung
5 konkrete Beispiele der Poisson-Verteilung
Online-Rechner zur Fischverteilung