So berechnen sie poisson-wahrscheinlichkeiten mit einem ti-84-rechner

Die Poisson-Verteilung ist eine der am häufigsten verwendeten Verteilungen in allen Statistiken. In diesem Tutorial wird erklärt, wie Sie die folgenden Funktionen auf einem TI-84-Rechner verwenden, um Poisson-Wahrscheinlichkeiten zu ermitteln:

Poissonpdf(mean, x) gibt die Wahrscheinlichkeit zurück, die dem Poisson-PDF zugeordnet ist.

Poissoncdf(mean, x) gibt die kumulative Wahrscheinlichkeit zurück, die dem Poisson-cdf zugeordnet ist.

Gold:

• Durchschnitt = durchschnittliche Anzahl an „Erfolgen“
• x = spezifische Anzahl an „Erfolgen“

Auf diese beiden Funktionen können Sie auf einem TI-84-Rechner zugreifen, indem Sie 2nd und dann vars drücken. Dadurch gelangen Sie zu einem DISTR- Bildschirm, auf dem Sie dann „fishpdf()“ und „fishcdf()“ verwenden können:

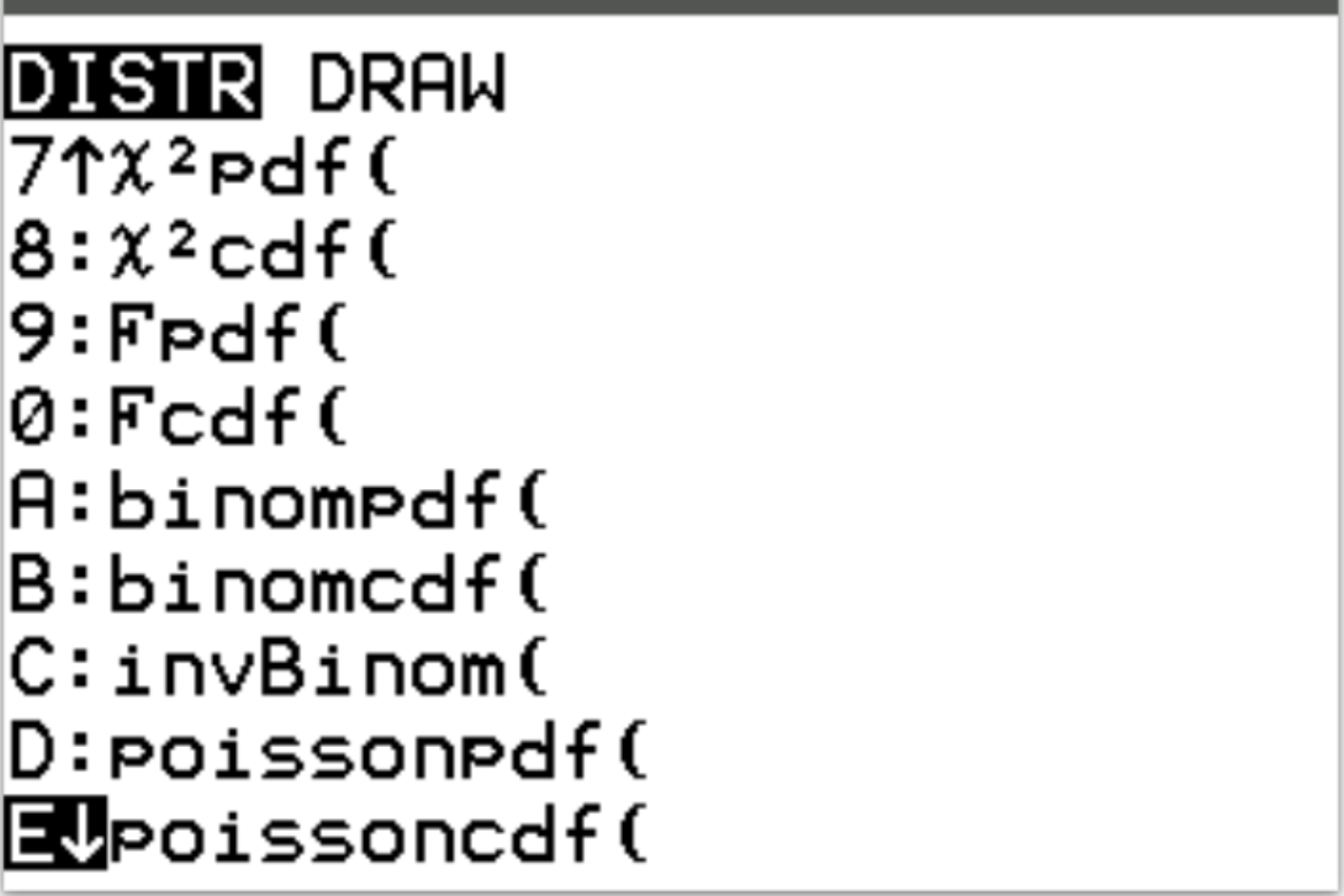
Die folgenden Beispiele veranschaulichen, wie Sie diese Funktionen zur Beantwortung verschiedener Fragen verwenden.

Beispiel 1: Poisson-Wahrscheinlichkeit für genau x Erfolg

Frage: Ein Baumarkt verkauft durchschnittlich 3 Hämmer pro Tag. Wie hoch ist die Wahrscheinlichkeit, dass sie an einem bestimmten Tag 5 Hämmer verkaufen?

Antwort: Verwenden Sie die Funktion Poissonpdf(mean, x):

Fischpdf(3, 5) = 0,1008

Beispiel 2: Poisson-Wahrscheinlichkeit für weniger als x Erfolg

Frage: Ein Baumarkt verkauft durchschnittlich 3 Hämmer pro Tag. Wie groß ist die Wahrscheinlichkeit, dass sie an einem bestimmten Tag weniger als 5 Hämmer verkaufen?

Antwort: Verwenden Sie die Funktion Poissoncdf(mean, x-1):

fishcdf(3, 4) = 0,8153

Beispiel 3: Poisson-Wahrscheinlichkeit für höchstens x Erfolg

Frage: Ein Baumarkt verkauft durchschnittlich 3 Hämmer pro Tag. Wie hoch ist die Wahrscheinlichkeit, dass sie an einem bestimmten Tag höchstens 5 Hämmer verkaufen?

Antwort: Verwenden Sie die Funktion Poissoncdf(mean, x):

fishcdf(3, 5) = 0,9161

Beispiel 4: Poisson-Wahrscheinlichkeit für mehr als x Erfolg

Frage: Ein Baumarkt verkauft durchschnittlich 3 Hämmer pro Tag. Wie groß ist die Wahrscheinlichkeit, dass sie an einem bestimmten Tag mehr als 5 Hämmer verkaufen?

Antwort: Verwenden Sie Funktion 1 – Poissoncdf(mean, x):

1 – fishcdf(3, 5) = 0,0839

Beispiel 5: Poisson-Wahrscheinlichkeit für mindestens x Erfolg

Frage: Ein Baumarkt verkauft durchschnittlich 3 Hämmer pro Tag. Wie hoch ist die Wahrscheinlichkeit, dass sie an einem bestimmten Tag mindestens 5 Hämmer verkaufen?

Antwort: Verwenden Sie Funktion 1 – Poissoncdf(mean, x-1):

1 – fishcdf(3, 4) = 0,1847