So verwenden sie fitdistr() in r, um verteilungen anzupassen

Sie können die Funktion fitdistr() aus dem MASS- Paket in R verwenden, um die Parameter einer Verteilung durch Maximieren der Likelihood-Funktion zu schätzen.

Diese Funktion verwendet die folgende grundlegende Syntax:

fitdistr(x, Densefun, …)

Gold:

• x : Ein numerischer Vektor, der die Werte der Verteilung darstellt
• Densefun : die Verteilung, für die die Parameter geschätzt werden sollen

Beachten Sie, dass das Densefun- Argument die folgenden möglichen Verteilungsnamen akzeptiert: Beta , Cauchy , Chi-Quadrat , Exponential , Gamma , Geometrisch , Lognormal , Logistisch , Negativ Binomial , Normal , Poisson , t und Weibull .

Das folgende Beispiel zeigt, wie die Funktion fitdistr() in der Praxis verwendet wird.

Beispiel: So verwenden Sie die Funktion fitdistr(), um Verteilungen in R anzupassen

Angenommen, wir verwenden die Funktion rnorm() in R, um einen Vektor mit 200 Werten zu generieren, der einer Normalverteilung folgt:

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

Mit der Funktion hist() können wir ein Histogramm erstellen, um die Verteilung von Datenwerten zu visualisieren:

 hist(data, col=' steelblue ')

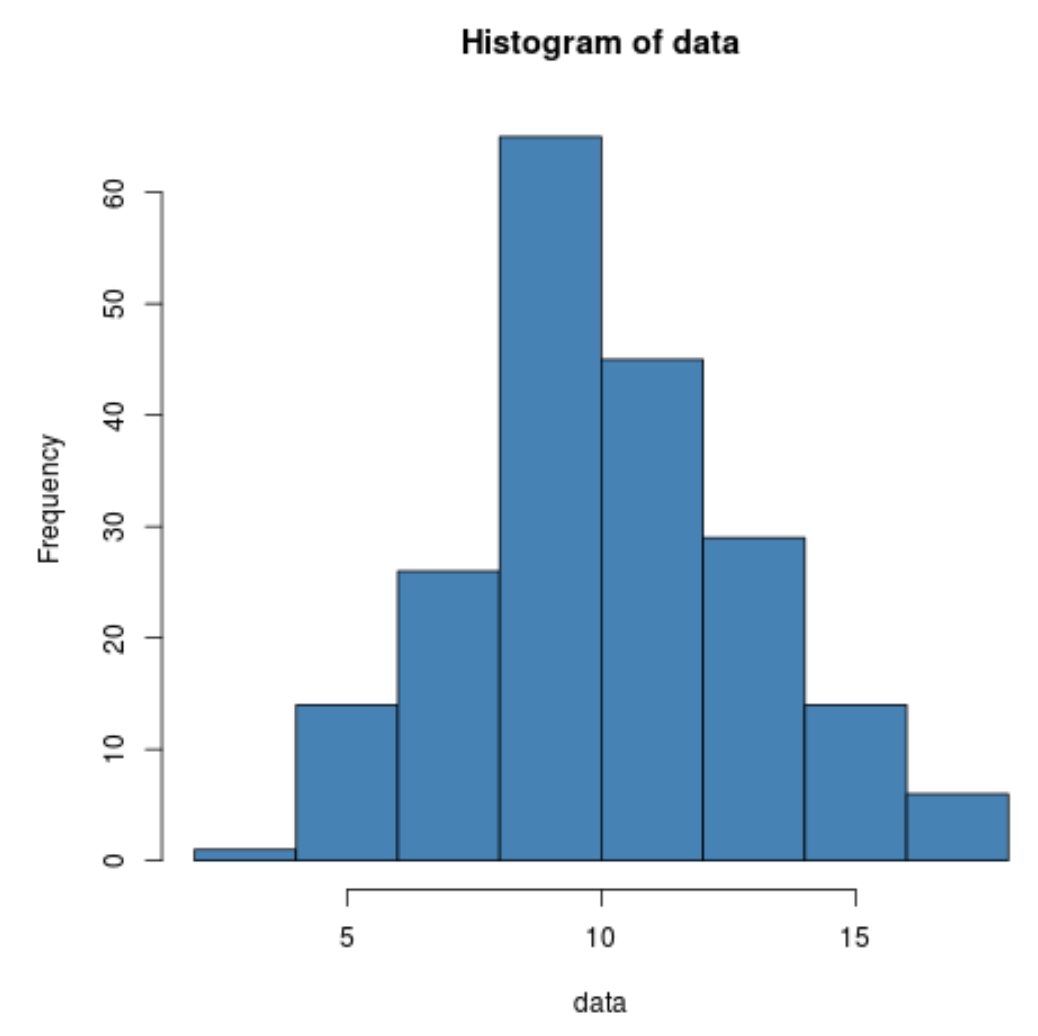
Wir können sehen, dass die Daten tatsächlich normalverteilt erscheinen.

Anschließend können wir die Funktion fitdistr() verwenden, um die Parameter dieser Verteilung abzuschätzen:

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

Die Funktion fitdistr() schätzt, dass der Wertevektor einer Normalverteilung mit einem Mittelwert von 10,1066189 und einer Standardabweichung von 2,7803148 folgt.

Diese Werte sollten nicht überraschen, da wir die Daten mit der Funktion rnorm() mit einem Mittelwert von 10 und einer Standardabweichung von 3 generiert haben.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in R ausführen:

So zeichnen Sie eine Normalverteilung in R auf
So erzeugen Sie eine Normalverteilung in R
So führen Sie einen Shapiro-Wilk-Test auf Normalität in R durch