Frequenzpolygon
In diesem Artikel wird erklärt, was ein Frequenzpolygon ist und wofür es verwendet wird. Darüber hinaus erfahren Sie, welche verschiedenen Arten von Frequenzpolygonen es gibt, und erhalten jeweils ein Beispiel.
Was ist ein Frequenzpolygon?
Ein Häufigkeitspolygon ist eine Art statistisches Diagramm, in dem der Datensatz durch Punkte dargestellt und durch Linien verbunden wird.
In der Statistik wird im Allgemeinen das Häufigkeitspolygon zur Darstellung einer Zeitreihe verwendet. Denn diese Art von Diagramm ist sehr nützlich für die Analyse der Datenentwicklung.
Das Häufigkeitspolygon kann durch Verbinden der Enden der Balken eines Balkendiagramms oder Histogramms erstellt werden. Im Folgenden werden wir sehen, wie das geht.
So erstellen Sie ein Frequenzpolygon
Die Schritte zum Erstellen eines Frequenzpolygons sind wie folgt:
- Zeichnen Sie die horizontale und vertikale Achse des Frequenzpolygons und erstellen Sie den Maßstab, damit Sie die Daten anschließend im Diagramm darstellen können.
- Stellen Sie die Datenpaare als Punkte im Diagramm dar.
- Verbinden Sie aufeinanderfolgende Punkte im Diagramm mithilfe einer Linie.
Beispiel für ein Frequenzpolygon
Damit Sie genau sehen können, wie ein Frequenzpolygon aufgebaut wird, finden Sie unten ein erläutertes Beispiel.
- In der folgenden Datentabelle ist der Aktienwert eines börsennotierten Unternehmens der letzten 10 Jahre zusammengestellt. Stellen Sie die Daten mithilfe eines Häufigkeitspolygons grafisch dar.
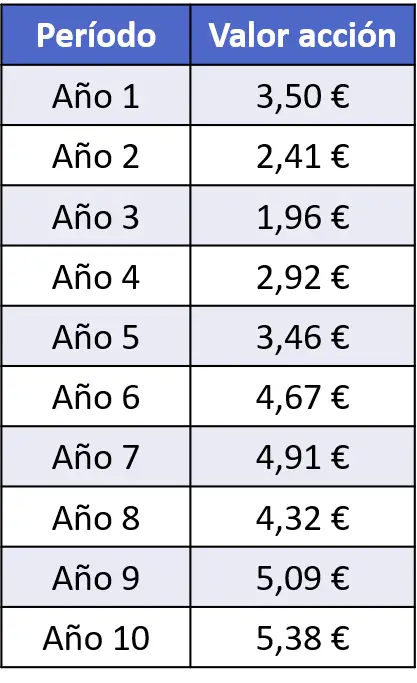
Zunächst müssen wir die Achsen des Frequenzpolygons darstellen. Auf der horizontalen Achse tragen wir die Zeiträume und auf der vertikalen Achse die Aktienkurse ein:
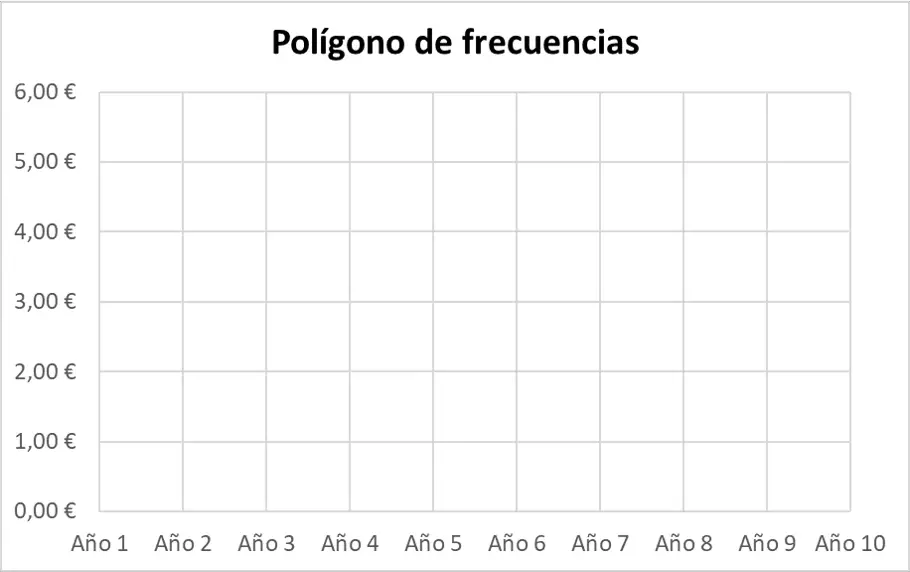
Zweitens stellen wir den statistischen Datensatz mit Punkten dar. Denken Sie daran, dass jeder Punkt im Diagramm dort dargestellt wird, wo sich die beiden imaginären Linien ihrer entsprechenden Werte auf den Achsen schneiden.
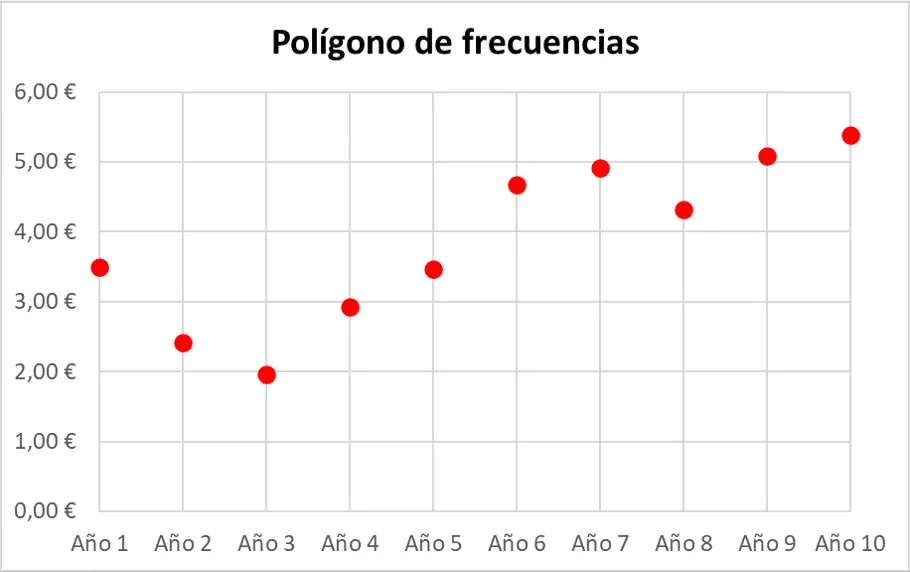
Zum Schluss verbinden Sie einfach die aufeinanderfolgenden Punkte mit einer geraden Linie und bilden so eine durchgehende Linie für das gesamte Frequenzpolygon.
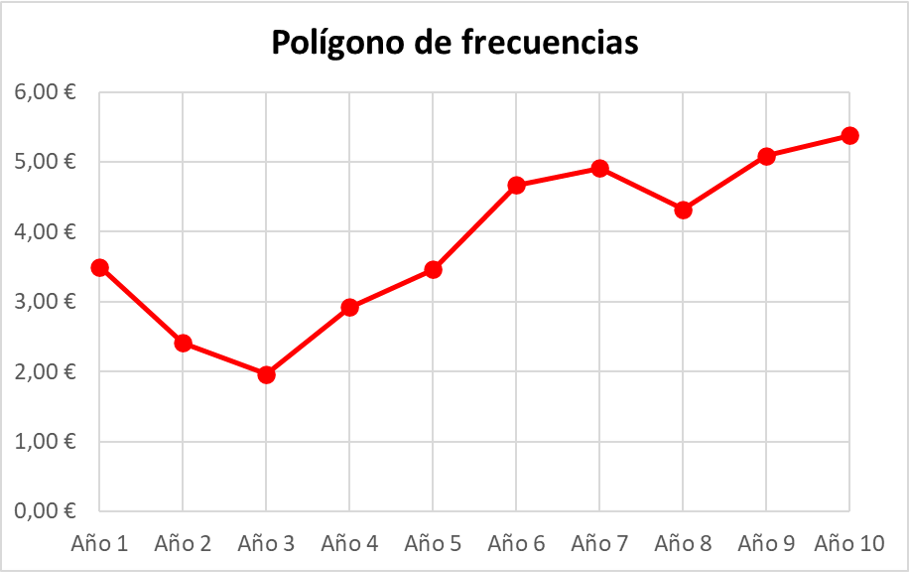
In diesem Fall wurden absolute Häufigkeiten im Häufigkeitspolygon dargestellt, es hätten aber auch relative (oder prozentuale) Häufigkeiten dargestellt werden können.
Häufigkeitspolygon für gruppierte Daten
Wir haben gerade gesehen, wie ein Häufigkeitspolygon erstellt wird, wenn die Variable diskret ist, aber ein Häufigkeitspolygon kann auch mit kontinuierlichen Variablen erstellt werden, d. h. wenn die Daten in Intervallen gruppiert sind. Unten sehen Sie ein solches gelöstes Beispiel.
- Die Stichprobengröße von 50 Personen wurde gemessen und die Daten in der folgenden Häufigkeitstabelle aufgezeichnet. Stellen Sie die Daten mithilfe eines Häufigkeitspolygons grafisch dar.
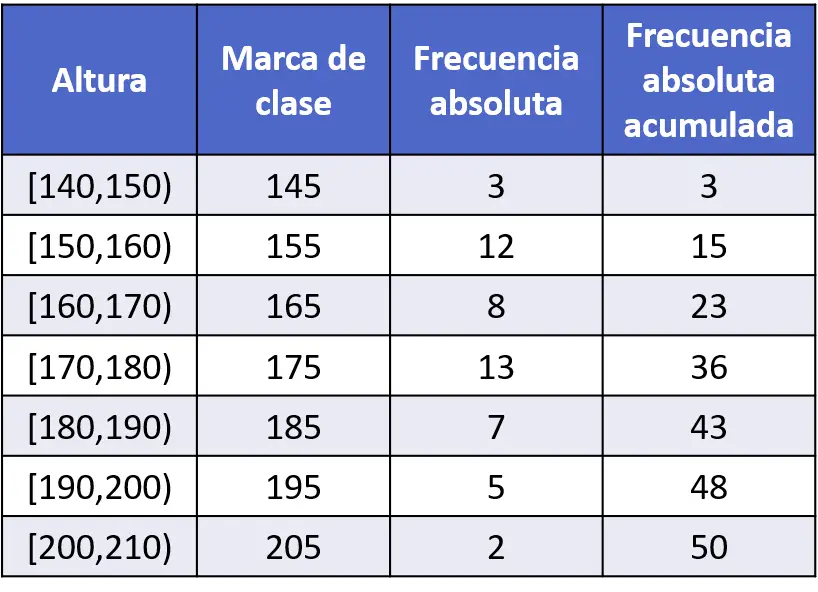
Da die Daten nach Intervallen gruppiert sind, sollten die Punkte des Häufigkeitspolygons an der Klassenmarkierung jedes Intervalls aufgetragen werden, d. h. am Mittelpunkt der Endpunkte des Intervalls.
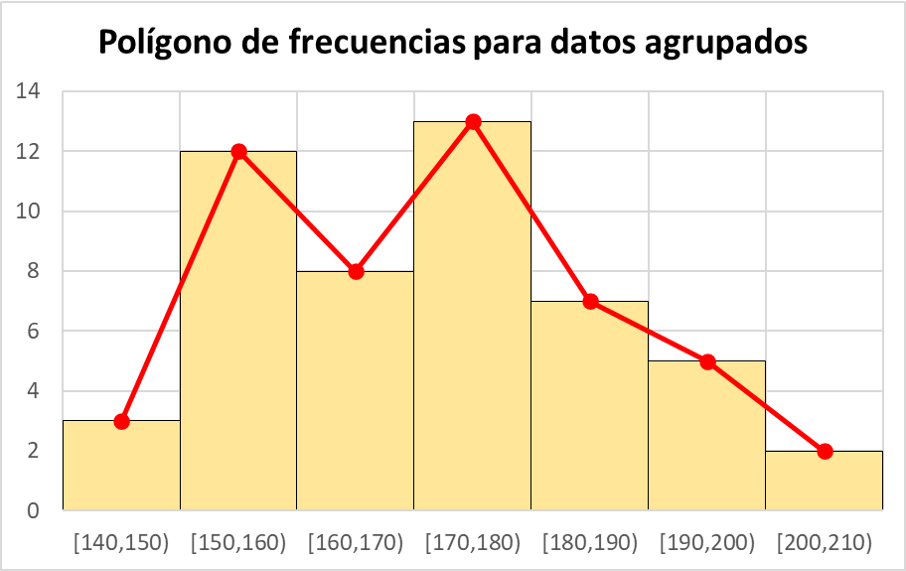
Wie das Diagramm zeigt, kann bei der Gruppierung von Daten das Häufigkeitspolygon mit einem Histogramm kombiniert werden. Wenn Sie zunächst das Histogramm erstellen, müssen Sie zum Zeichnen des Häufigkeitspolygons lediglich die Mittelpunkte jedes rechteckigen Balkens im Histogramm verbinden.
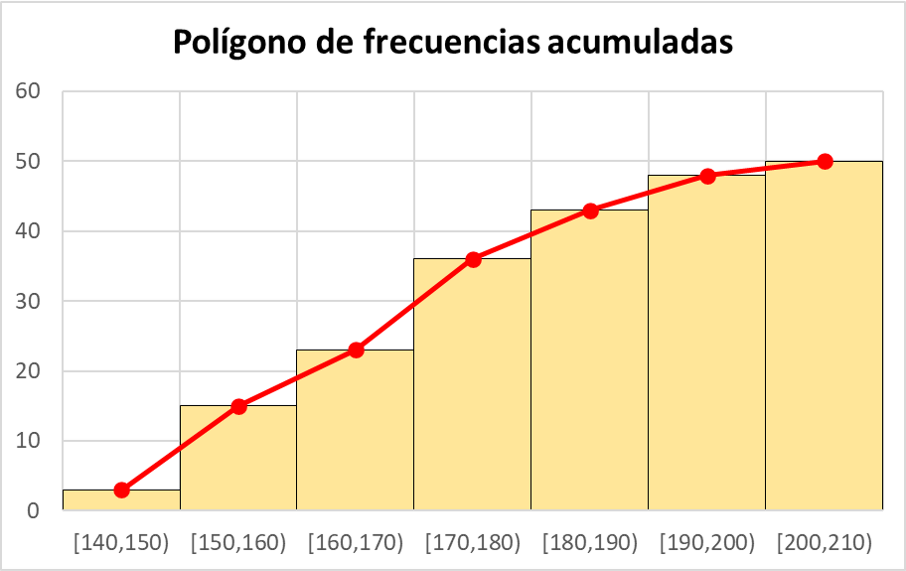
Kumulatives Häufigkeitspolygon
In der Statistik wird das Häufigkeitspolygon auch zur Darstellung von Summenhäufigkeiten verwendet. Berechnen Sie einfach zuerst die kumulativen Häufigkeiten des Datensatzes und verwenden Sie dann die kumulativen Häufigkeiten anstelle der absoluten Häufigkeiten, um die Punkte im Häufigkeitspolygon darzustellen.
Denken Sie daran, dass die kumulative absolute Häufigkeit durch Addition aller vorherigen absoluten Häufigkeiten plus der absoluten Häufigkeit des Intervalls selbst berechnet wird.
Als Beispiel sehen Sie unten das kumulative absolute Häufigkeitspolygon aus dem Datensatz aus der vorherigen Übung: