Friedman-test: definition, formel und beispiel

Der Friedman-Test ist eine nichtparametrische Alternative zur ANOVA mit wiederholten Messungen .

Es wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht, in denen in jeder Gruppe dieselben Probanden vorkommen.

Wann ist der Friedman-Test anzuwenden?

Der Friedman-Test wird üblicherweise in zwei Situationen verwendet:

1. Messen Sie die durchschnittlichen Ergebnisse der Probanden über drei oder mehr Zeitpunkte.

Beispielsweise möchten Sie möglicherweise die verbleibende Herzfrequenz der Probanden einen Monat vor Beginn eines Trainingsprogramms, einen Monat nach Beginn des Programms und zwei Monate nach Verwendung des Programms messen. Sie können den Friedman-Test durchführen, um zu sehen, ob zu diesen drei Zeitpunkten ein signifikanter Unterschied in der durchschnittlichen verbleibenden Herzfrequenz des Patienten besteht.

2. Messen Sie die durchschnittlichen Ergebnisse der Probanden unter drei verschiedenen Bedingungen.

Beispielsweise könnten Sie Probanden bitten, sich drei verschiedene Filme anzusehen und jeden davon danach zu bewerten, wie gut er ihnen gefallen hat. Da jedes Thema in jeder Stichprobe vorkommt, können Sie einen Friedman-Test durchführen, um zu sehen, ob es einen signifikanten Unterschied in der durchschnittlichen Bewertung der drei Filme gibt.

Friedman-Test: Beispiel

Angenommen, wir möchten wissen, ob die durchschnittliche Reaktionszeit von Probanden auf drei verschiedene Medikamente unterschiedlich ist. Um dies zu testen, rekrutieren wir 10 Patienten und messen jede ihrer Reaktionszeiten (in Sekunden) auf die drei verschiedenen Medikamente. Nachfolgend werden die Ergebnisse für jeden Patienten dargestellt:

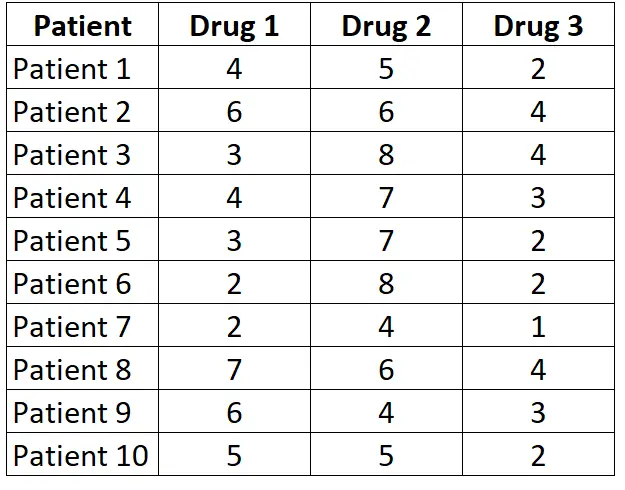
Da bei jedem Patienten jedes der drei Medikamente gemessen wird, verwenden wir den Friedman-Test, um festzustellen, ob sich die durchschnittliche Reaktionszeit zwischen den drei Medikamenten unterscheidet.

Schritt 1. Formulieren Sie die Hypothesen.

Die Nullhypothese (H ₀ ): µ ₁ = µ ₂ = µ ₃ (die durchschnittlichen Reaktionszeiten aller Populationen sind alle gleich)

Die Alternativhypothese: (Ha): Mindestens ein Populationsmittelwert unterscheidet sich vom Rest

Schritt 2. Führen Sie den Friedman-Test durch.

Wir verwenden den Friedman-Testrechner mit der folgenden Eingabe:

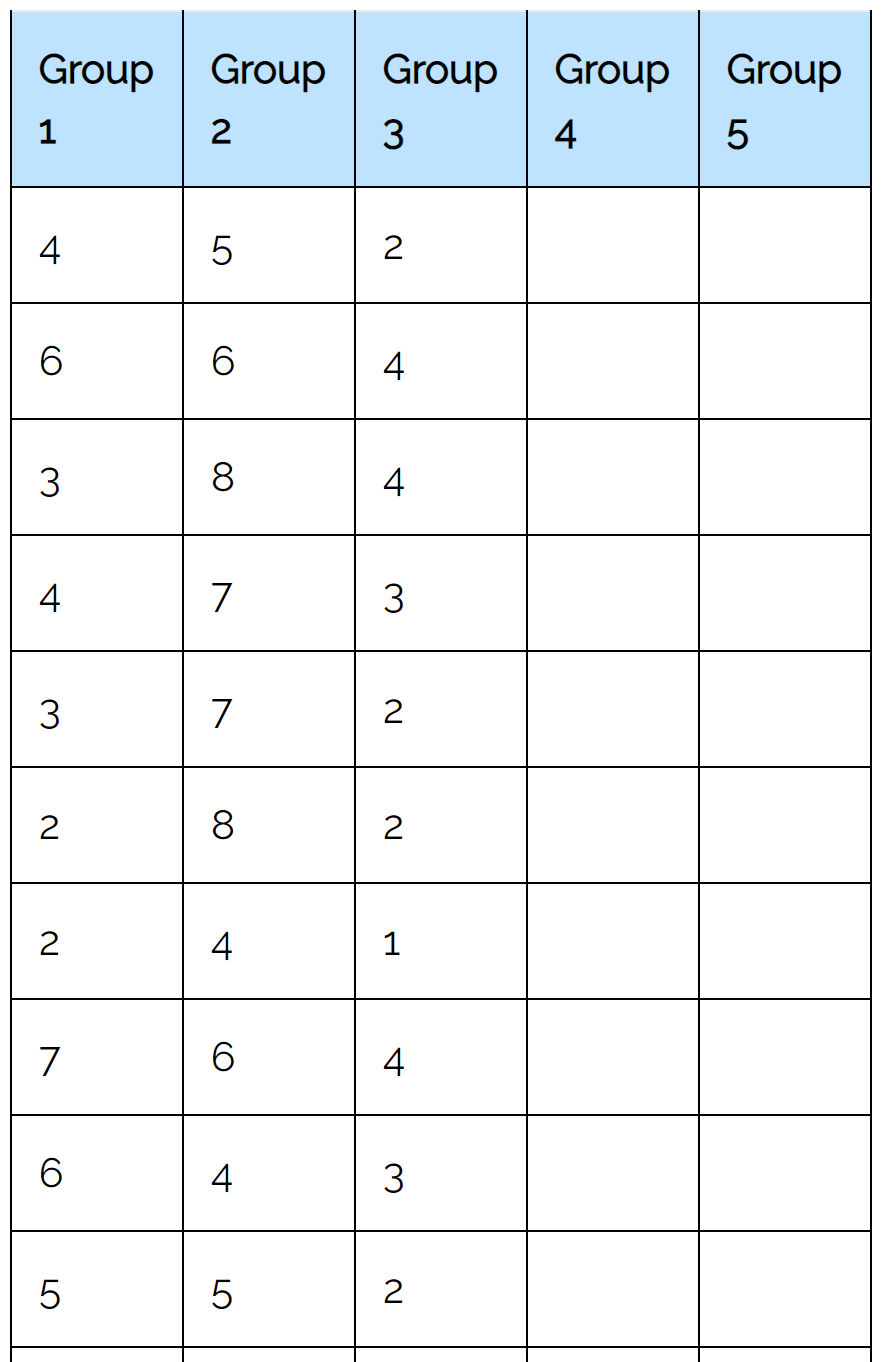
Sobald wir auf „Berechnen“ klicken, erscheint automatisch folgendes Ergebnis:

Schritt 3: Interpretieren Sie die Ergebnisse.

Die Teststatistik ist Q = 12,35 und der entsprechende p-Wert ist p = 0,00208 . Da dieser Wert kleiner als 0,05 ist, können wir die Nullhypothese zurückweisen, dass die durchschnittliche Reaktionszeit für alle drei Medikamente gleich ist.

Wir haben genügend Beweise, um zu dem Schluss zu kommen, dass die Art der verwendeten Medikamente zu statistisch signifikanten Unterschieden in der Reaktionszeit führt.

Schritt 4: Melden Sie die Ergebnisse.

Abschließend möchten wir Ihnen die Testergebnisse mitteilen. Hier ist ein Beispiel dafür:

An 10 Patienten wurde ein Friedman-Test durchgeführt, um die Wirkung von drei verschiedenen Medikamenten auf die Reaktionszeit zu untersuchen. Jeder Patient verwendete jedes Medikament einmal.

Die Ergebnisse zeigten, dass die Art der verwendeten Medikamente zu statistisch signifikanten Unterschieden in der Reaktionszeit führte (Q = 12,35, p = 0,00208).

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie den Friedman-Test mit unterschiedlicher Statistiksoftware durchführen:

So führen Sie den Friedman-Test in Excel durch
So führen Sie den Friedman-Test in R durch
So führen Sie den Friedman-Test in Python durch
So führen Sie den Friedman-Test in Stata durch
Online-Friedman-Testrechner