Gammaverteilung
In diesem Artikel wird erklärt, was die Gammaverteilung ist und wofür sie verwendet wird. So finden Sie die Definition der Gammaverteilung, ihre Eigenschaften und wie ihre grafische Darstellung aussieht.
Was ist die Gammaverteilung?
Die Gammaverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die durch zwei charakteristische Parameter, α und λ, definiert wird. Mit anderen Worten: Die Gammaverteilung hängt vom Wert ihrer beiden Parameter ab: α ist der Formparameter und λ der Skalenparameter.
Das Symbol für die Gammaverteilung ist der griechische Großbuchstabe Γ. Wenn also eine Zufallsvariable einer Gammaverteilung folgt, wird sie wie folgt geschrieben:
![]()
Die Gammaverteilung kann auch mit dem Formparameter k = α und dem inversen Skalenparameter θ = 1/λ parametrisiert werden. In allen Fällen sind die beiden Parameter, die die Gammaverteilung definieren, positive reelle Zahlen.
Typischerweise wird die Gammaverteilung zur Modellierung rechtsschiefer Datensätze verwendet, sodass auf der linken Seite des Diagramms eine größere Datenkonzentration vorliegt. Beispielsweise wird die Gammaverteilung zur Modellierung der Zuverlässigkeit elektrischer Komponenten verwendet.
Gamma-Verteilungsdiagramm
Der Graph der Gammaverteilung hängt von den Werten seiner charakteristischen Parameter ab. Unten sehen Sie, wie die Dichtefunktion der Gammaverteilung je nach Formparameter und Skalenparameter variiert.
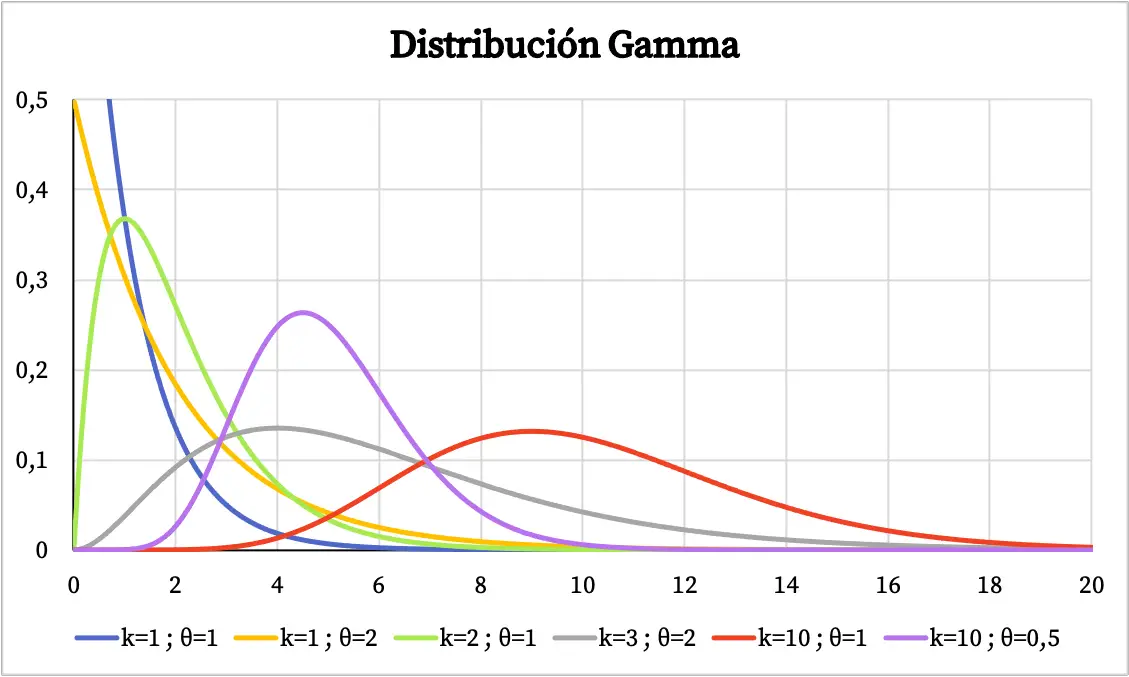
Andererseits können Sie unten die Grafik der kumulativen Wahrscheinlichkeitsfunktion der Gammaverteilung sehen:
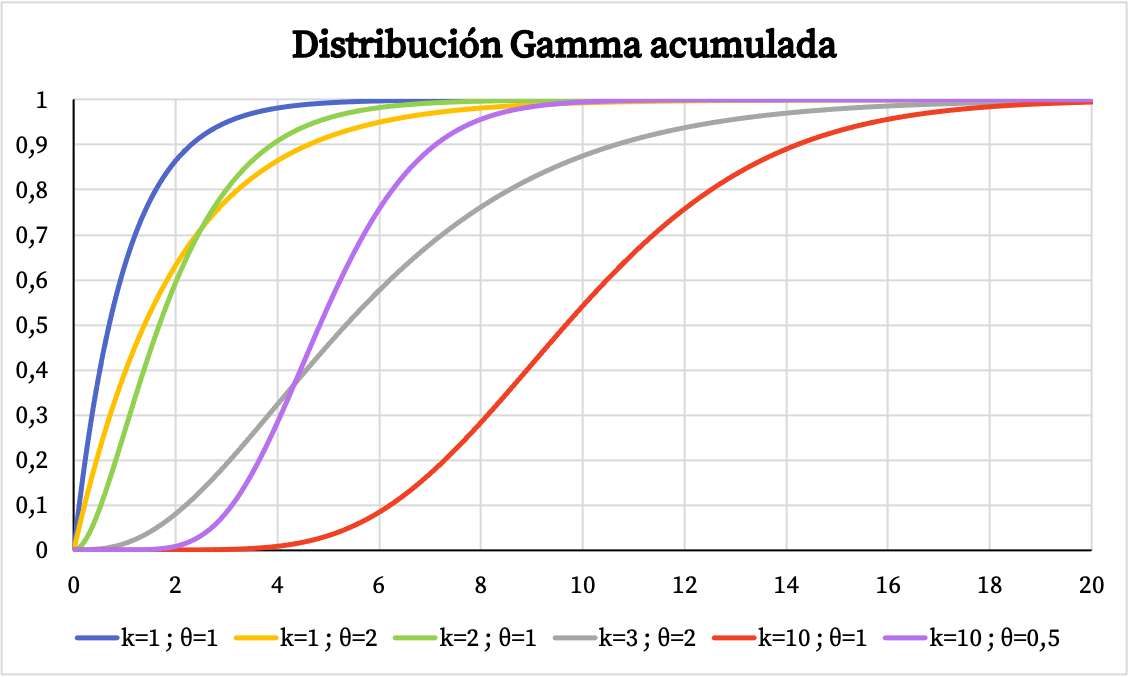
Eigenschaften der Gammaverteilung
Wir werden dann sehen, was die Eigenschaften der Gammaverteilung sind.
- Der Graph der Gammaverteilung wird vollständig durch seine beiden charakteristischen Parameter definiert: α ist der Formparameter und λ ist der Skalenparameter.
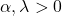
![]()
- Der Mittelwert der Gammaverteilung ist gleich dem Verhältnis zwischen dem Formparameter und dem Skalenparameter, also α/λ.
![]()
- Die Varianz der Gammaverteilung entspricht dem Formparameter dividiert durch das Quadrat des Skalenparameters.
![]()
- Für Werte von α kleiner als 1 ist der Modus 0. Wenn α jedoch gleich oder größer als 1 ist, kann der Modus der Gammaverteilung mit der folgenden Formel berechnet werden:
![Rendered by QuickLaTeX.com \begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9e2762af62f9c38870902ec0284ee07_l3.png)
- Die Formel für die Dichtefunktion der Gammaverteilung lautet:
![]()
Wobei Γ die Gammafunktion ist, die definiert ist als:
![]()
- Die Formel für die kumulative Verteilung einer durch eine Gammaverteilung definierten Zufallsvariablen lautet wie folgt:
![]()
- Wenn der Formparameter α gleich 1 ist, dann entspricht die Gammaverteilung einer Exponentialverteilung mit demselben Skalenparameter λ.
![]()
- Wenn der Skalenparameter λ ein Durchschnitt ist, ist die Gammaverteilung ein Sonderfall der Chi-Quadrat-Verteilung .
![]()