So interpretieren sie ein gekrümmtes residuendiagramm (mit beispiel)

Mithilfe von Residuendiagrammen wird beurteilt, ob die Residuen eines Regressionsmodells normalverteilt sind und ob sie Heteroskedastizität aufweisen.

Idealerweise möchten Sie, dass die Punkte in einem Residuendiagramm zufällig um einen Wert von Null herum verstreut sind und kein klares Muster aufweisen.

Wenn Sie auf ein Residuendiagramm stoßen, in dem die Diagrammpunkte ein gekrümmtes Muster aufweisen, bedeutet dies wahrscheinlich, dass das von Ihnen für die Daten angegebene Regressionsmodell nicht korrekt ist.

In den meisten Fällen bedeutet dies, dass Sie versucht haben, ein lineares Regressionsmodell an einen Datensatz anzupassen, der stattdessen einem quadratischen Trend folgt.

Das folgende Beispiel zeigt, wie ein gekrümmtes Residuendiagramm in der Praxis interpretiert (und korrigiert) wird.

Beispiel: Interpretation eines gekrümmten Residuendiagramms

Angenommen, wir erfassen die folgenden Daten zur Anzahl der pro Woche geleisteten Arbeitsstunden und zum gemeldeten Grad der Zufriedenheit (auf einer Skala von 0 bis 100) für 11 verschiedene Personen in einem Büro:

Wenn wir ein einfaches Streudiagramm der geleisteten Arbeitsstunden im Verhältnis zum Zufriedenheitsgrad erstellen würden, würde es so aussehen:

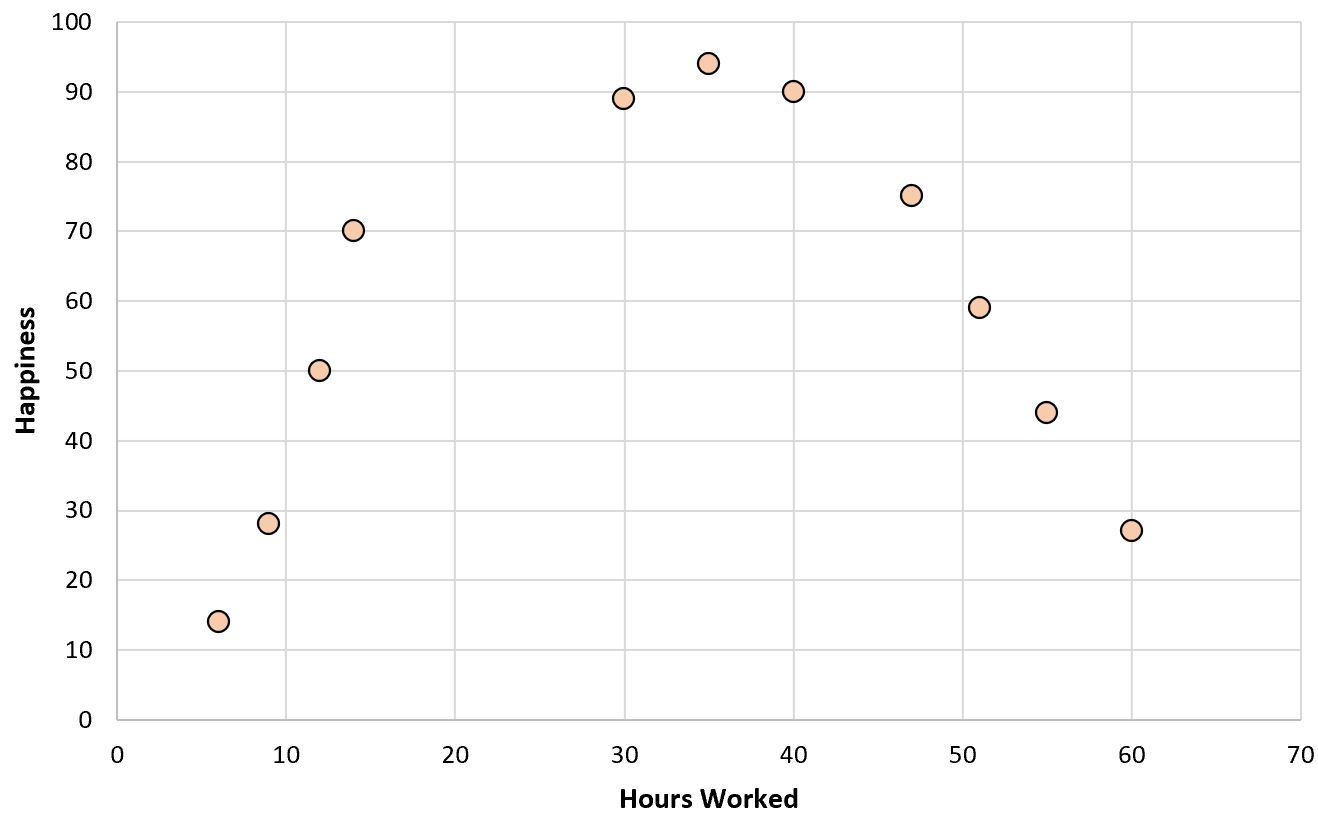
Nehmen wir nun an, wir möchten ein Regressionsmodell anhand der geleisteten Arbeitsstunden anpassen, um das Glücksniveau vorherzusagen.

Der folgende Code zeigt, wie man ein einfaches lineares Regressionsmodell an diesen Datensatz anpasst und ein Residuendiagramm in R erstellt:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

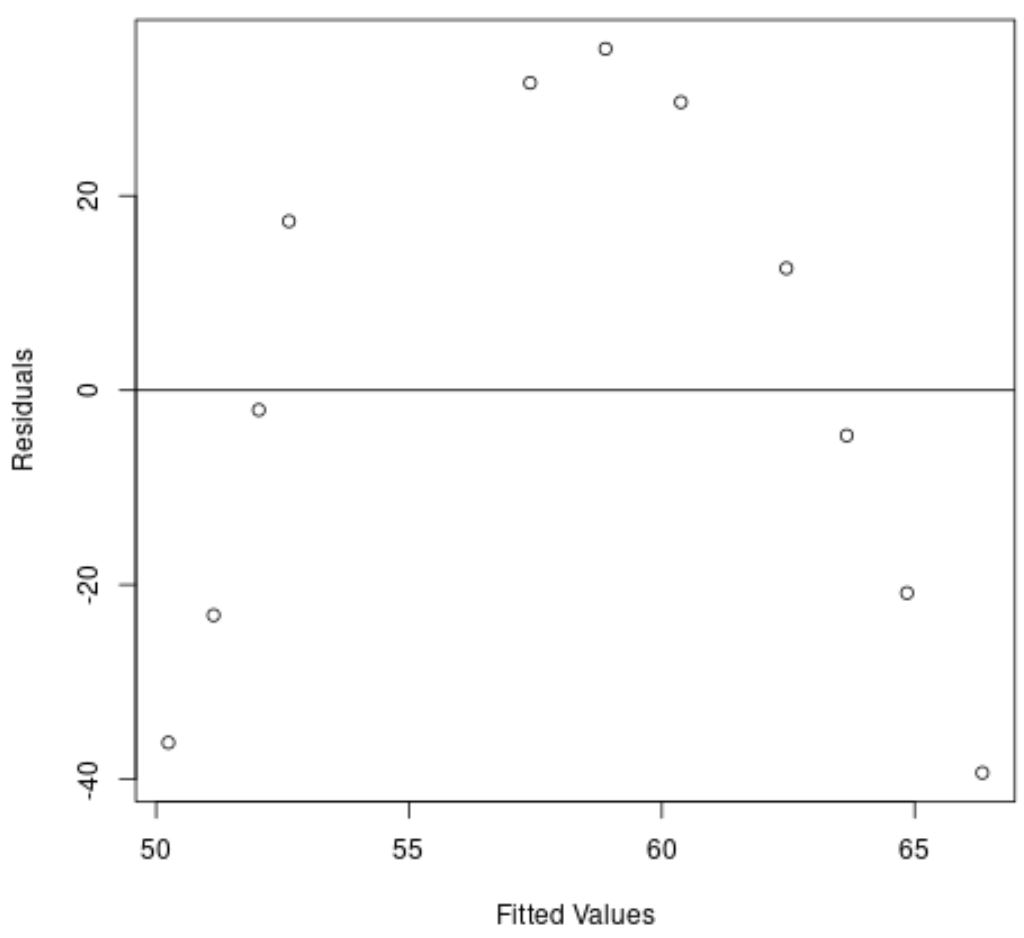
Die x-Achse zeigt die angepassten Werte und die y-Achse zeigt die Residuen an.

Aus der Grafik können wir erkennen, dass die Residuen ein gekrümmtes Muster aufweisen, was darauf hindeutet, dass ein lineares Regressionsmodell keine geeignete Anpassung an diesen Datensatz bietet.

Der folgende Code zeigt, wie man ein quadratisches Regressionsmodell an diesen Datensatz anpasst und ein Residuendiagramm in R erstellt:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

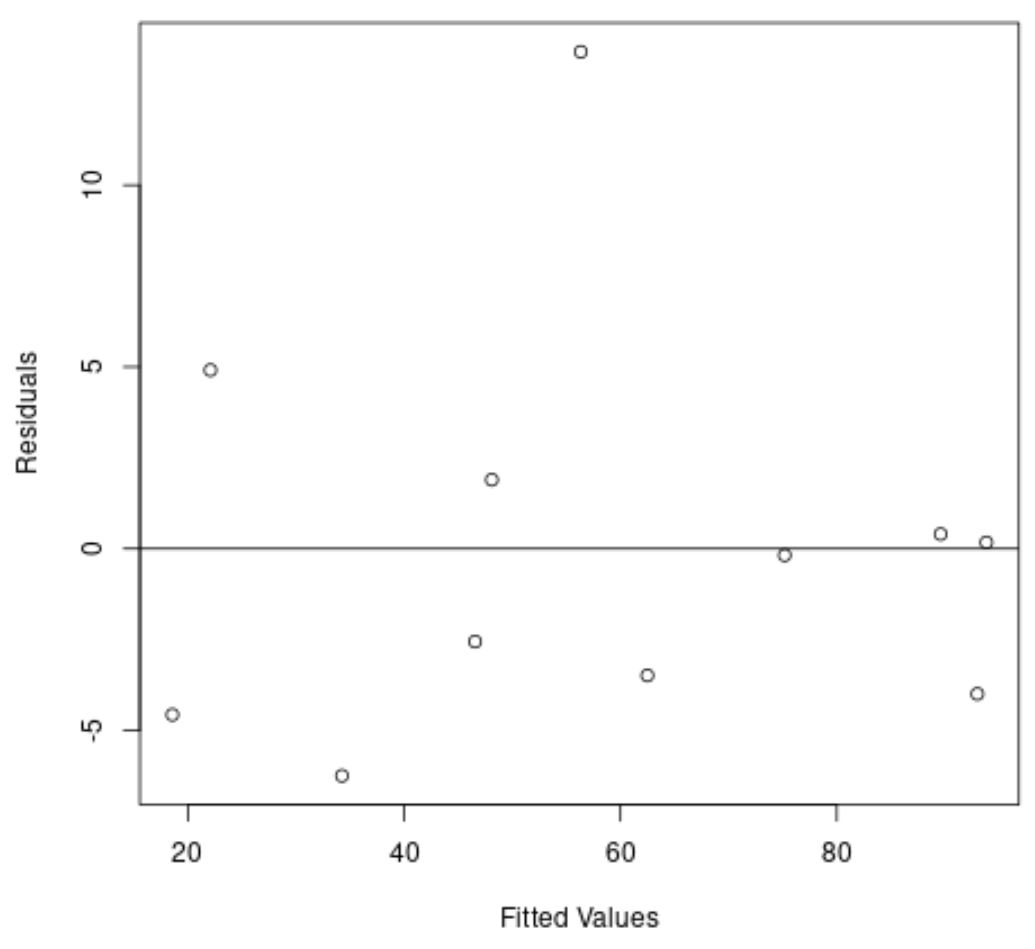
Auch hier zeigt die x-Achse die angepassten Werte und die y-Achse die Residuen.

Aus dem Diagramm können wir ersehen, dass die Residuen zufällig um Null herum verstreut sind und es keinen klaren Trend bei den Residuen gibt.

Dies zeigt uns, dass ein quadratisches Regressionsmodell diesen Datensatz viel besser anpassen kann als ein lineares Regressionsmodell.

Dies sollte angesichts der Tatsache, dass wir gesehen haben, dass der tatsächliche Zusammenhang zwischen geleisteten Arbeitsstunden und dem Grad der Zufriedenheit eher quadratisch als linear zu sein scheint, Sinn ergeben.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie mit unterschiedlicher Statistiksoftware Residuendiagramme erstellen:

So erstellen Sie manuell einen Restpfad
So erstellen Sie ein Residuendiagramm in R
So erstellen Sie ein Residuendiagramm in Excel
So erstellen Sie ein Restdiagramm in Python