Was ist eine gemeinsame wahrscheinlichkeitsverteilung?

Eine bidirektionale Häufigkeitstabelle ist eine Tabelle, die die Häufigkeiten (oder „Zählungen“) für zwei kategoriale Variablen anzeigt.

Die folgende Zwei-Wege-Tabelle zeigt beispielsweise die Ergebnisse einer Umfrage, bei der 100 Personen gefragt wurden, welche Sportart sie bevorzugen: Baseball, Basketball oder Fußball.

In den Zeilen wird das Geschlecht des Befragten angezeigt und in den Spalten die von ihm gewählte Sportart:

In diesem Beispiel gibt es zwei Variablen: Sport und Geschlecht.

Eine gemeinsame Wahrscheinlichkeitsverteilung beschreibt einfach die Wahrscheinlichkeit, dass eine bestimmte Person zwei bestimmte Werte für die Variablen annimmt.

Das Wort „Konjunktion“ kommt daher, dass wir an der Wahrscheinlichkeit interessiert sind, dass zwei Dinge gleichzeitig passieren.

Beispielsweise waren von insgesamt 100 Personen 13 männlich und wählten Baseball als ihren Lieblingssport.

Wir würden also sagen, dass die gemeinsame Wahrscheinlichkeit, dass eine bestimmte Person männlich ist und Baseball als ihren Lieblingssport wählt, 13/100 = 0,13 oder 13 % beträgt.

In mathematischer Notation geschrieben:

P(Geschlecht = Männlich, Sport = Baseball) = 13/100 = 0,13 .

Mit diesem Verfahren können wir die gesamte gemeinsame Wahrscheinlichkeitsverteilung berechnen:

• P (Geschlecht = männlich, Sport = Baseball) = 13/100 = 0,13
• P(Geschlecht = Männlich, Sport = Basketball) = 15/100 = 0,15
• P(Geschlecht = Männlich, Sport = Fußball) = 20/100 = 0,20
• P (Geschlecht = weiblich, Sport = Baseball) = 23/100 = 0,23
• P(Geschlecht = weiblich, Sport = Basketball) = 16/100 = 0,16
• P(Geschlecht = weiblich, Sport = Fußball) = 13/100 = 0,13

Beachten Sie, dass die Summe der Wahrscheinlichkeiten 1 oder 100 % beträgt.

Warum eine gemeinsame Wahrscheinlichkeitsverteilung verwenden?

Gemeinsame Wahrscheinlichkeitsverteilungen sind nützlich, da wir häufig Daten für zwei Variablen (wie Sport und Geschlecht) sammeln und Fragen zu beiden Variablen beantworten möchten.

Beispielsweise möchten wir möglicherweise die Wahrscheinlichkeit verstehen, dass eine bestimmte Person in einer Population männlich ist und Baseball als Lieblingssport bevorzugt.

Oder wir möchten die Wahrscheinlichkeit verstehen, dass eine bestimmte Person weiblich ist und Fußball als Lieblingssport bevorzugt.

Eine gemeinsame Wahrscheinlichkeitsverteilung kann uns bei der Beantwortung dieser Fragen helfen.

Nutzen Sie die folgenden Beispiele als Übung, um gemeinsame Wahrscheinlichkeitsverteilungen besser zu verstehen.

Beispiel 1

Die folgende Zwei-Wege-Tabelle stellt die Ergebnisse einer Umfrage dar, bei der 238 Personen gefragt wurden, welche Art von Film sie bevorzugen:

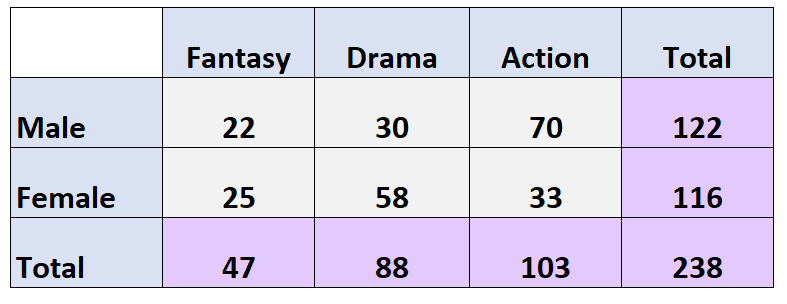
Frage: Wie groß ist die Wahrscheinlichkeit, dass eine bestimmte Person weiblich ist und Drama als ihr Lieblingsfilmgenre bevorzugt?

Antwort: P (Geschlecht = weiblich, Geschlecht = Drama) = 58/238 = 0,244 = 24,4 %

Beispiel 2

Die folgende Zwei-Wege-Tabelle zeigt die Prüfungsergebnisse von 64 Schülern einer Klasse basierend auf der Anzahl der Stunden, die sie mit dem Lernen verbracht haben:

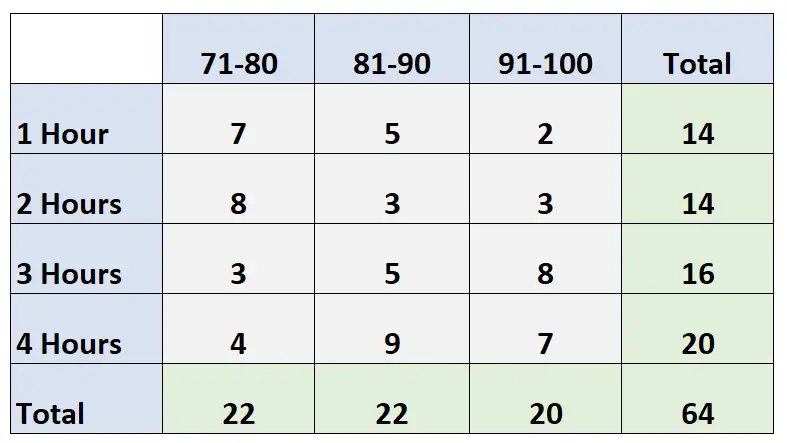
Frage: Wie hoch ist die Wahrscheinlichkeit, dass eine bestimmte Person zwei Stunden lang lernt und eine Note zwischen 91 und 100 erhält?

Antwort: P (Lernen = 2 Stunden, Ergebnis = 91–100) = 3/64 = 0,047 = 4,7 %

Zusätzliche Ressourcen

Was ist eine Randverteilung?
So ermitteln Sie die bedingte relative Häufigkeit in einer Tabelle mit doppeltem Eintrag