Exakter fisher-test: definition, formel und beispiel
Der exakte Fisher-Test wird verwendet, um zu bestimmen, ob zwischen zwei kategorialen Variablen ein signifikanter Zusammenhang besteht oder nicht. Er wird im Allgemeinen als Alternative zumChi-Quadrat-Unabhängigkeitstest verwendet, wenn eine oder mehrere Zellenzahlen in einer 2 × 2-Tabelle weniger als 5 betragen.
Der exakte Fisher-Test verwendet die folgenden Null- und Alternativhypothesen:
- H 0 : (Nullhypothese) Die beiden Variablen sind unabhängig.
- H 1 : (Alternativhypothese) Die beiden Variablen sind nicht unabhängig.
Angenommen, wir haben die folgende 2×2-Tabelle:
| Gruppe 1 | Gruppe 2 | Zeilensumme | |
| Kategorie 1 | HAT | B | a+b |
| Kategorie 2 | vs. | D | c+d |
| Gesamtspalte | a+c | b+d | a+b+c+d = n |
Der einseitige p-Wert für den exakten Fisher-Test wird wie folgt berechnet:
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
Dies ergibt denselben p-Wert wie der CDF der hypergeometrischen Verteilung mit den folgenden Parametern:
- Bevölkerungsgröße = n
- „Erfolg“ der Bevölkerung = a+b
- Stichprobengröße = a + c
- Beispiele für „Erfolg“ = eins
Der zweiseitige p-Wert für den exakten Fisher-Test ist weniger einfach zu berechnen und kann nicht durch einfache Multiplikation des einseitigen p-Werts mit zwei ermittelt werden. Um den zweiseitigen p-Wert zu ermitteln, empfehlen wir die Verwendungdes exakten Testrechners von Fisher .
Exakter Fisher-Test: Beispiel
Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz für eine politische Partei zusammenhängt oder nicht. Wir nehmen eine einfache Zufallsstichprobe von 25 Wählern und befragen sie zu ihrer Präferenz für eine politische Partei. Die folgende Tabelle stellt die Ergebnisse der Umfrage dar:
| Demokrat | Republikaner | Gesamt | |
| Männlich | 4 | 9 | 13 |
| Weiblich | 8 | 4 | 12 |
| Gesamt | 12 | 13 | 25 |
Schritt 1: Annahmen definieren.
Wir werden den exakten Fisher-Test unter Verwendung der folgenden Annahmen durchführen:
- H 0 : Geschlecht und politische Parteipräferenzen sind unabhängig.
- H 1 : Geschlecht und politische Parteipräferenzen sind nicht unabhängig.
Schritt 2: Berechnung des zweiseitigen p-Werts.
Wir können denFisher-Rechner für exakte Tests mit der folgenden Eingabe verwenden:
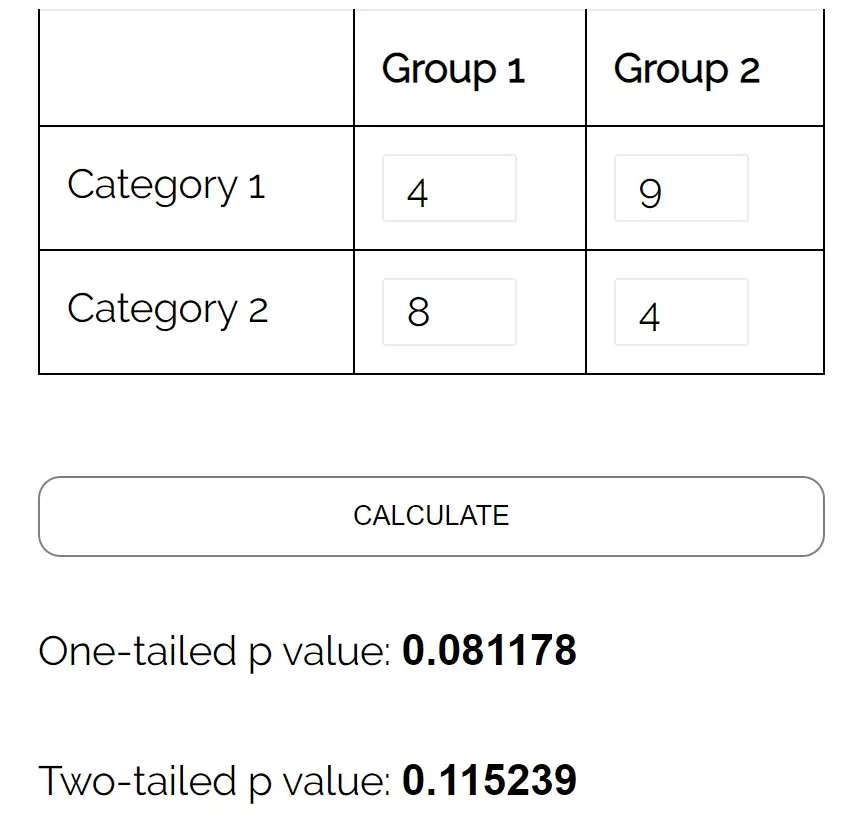
Der zweiseitige p-Wert beträgt 0,115239 . Da dieser Wert kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben keine ausreichenden Beweise dafür, dass es einen statistisch signifikanten Zusammenhang zwischen Geschlecht und Präferenz für eine politische Partei gibt.
Zusätzliche Ressourcen
In den folgenden Tutorials wird erläutert, wie Sie mit verschiedenen Statistikprogrammen einen exakten Fisher-Test durchführen:
So führen Sie den exakten Fisher-Test in R durch
So führen Sie den exakten Fisher-Test in Excel durch
So führen Sie den exakten Fisher-Test in Stata durch
So führen Sie den exakten Fisher-Test in SPSS durch
So führen Sie den genauen Fisher-Test in Python durch
Fishers exakter Testrechner