So führen sie den exakten fisher-test in excel durch

Der exakte Fisher-Test wird verwendet, um zu bestimmen, ob zwischen zwei kategorialen Variablen ein signifikanter Zusammenhang besteht oder nicht. Er wird im Allgemeinen als Alternative zum Chi-Quadrat-Unabhängigkeitstest verwendet, wenn eine oder mehrere Zellenzahlen in einer 2 × 2-Tabelle weniger als 5 betragen.

In diesem Tutorial wird erläutert, wie Sie den exakten Fisher-Test in Excel durchführen.

Beispiel: Exakter Fisher-Test in Excel

Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz für eine politische Partei an einer bestimmten Hochschule zusammenhängt. Um dies herauszufinden, befragen wir stichprobenartig 25 Studierende auf dem Campus. Die Anzahl der demokratischen oder republikanischen Studenten, basierend auf ihrem Geschlecht, ist in der folgenden Tabelle aufgeführt:

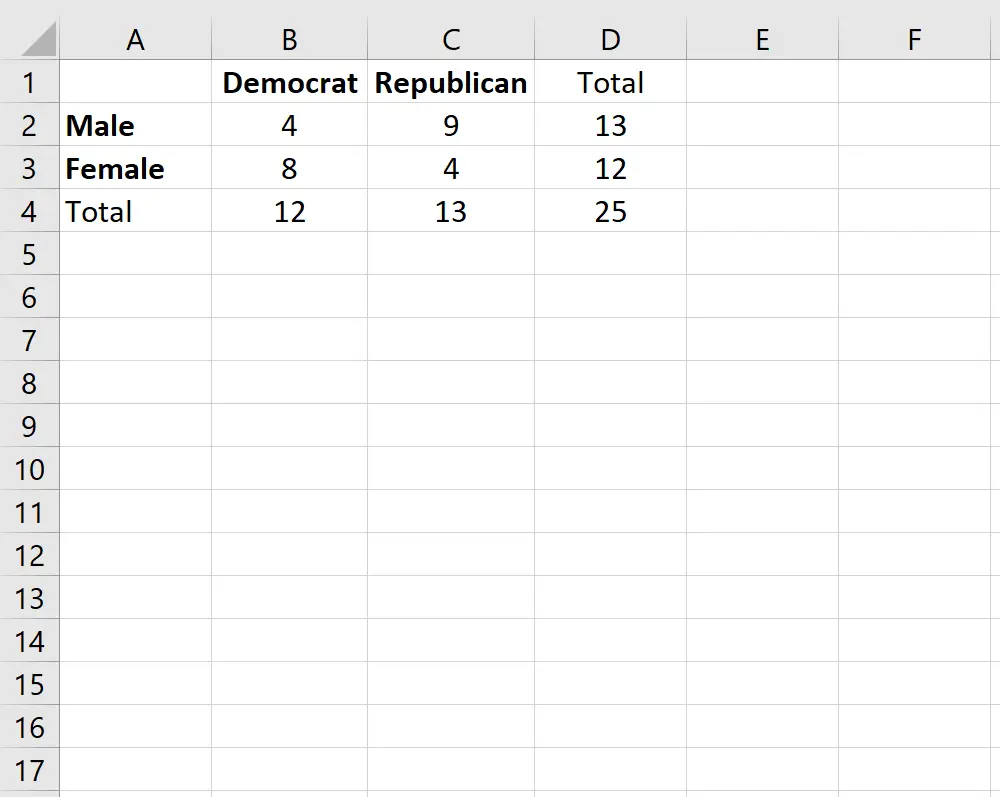
Um festzustellen, ob ein statistisch signifikanter Zusammenhang zwischen Geschlecht und Parteipräferenz besteht, können wir den exakten Fisher-Test durchführen.

Obwohl Excel nicht über eine integrierte Funktion zur Durchführung dieses Tests verfügt, können wir zur Durchführung des Tests die hypergeometrische Funktion verwenden, die die folgende Syntax verwendet:

=HYPGEOM.DIST(sample_s, number_sample, population_s, number_pop, kumulativ)

Gold:

• sample_s = die Anzahl der „Erfolge“ in der Stichprobe
• number_sample = Stichprobengröße
• Population_s = die Anzahl der „Erfolge“ in der Population
• number_pop = Bevölkerungsgröße
• kumulativ = wenn TRUE, gibt dies die kumulative Verteilungsfunktion zurück; wenn FALSE, gibt dies die Wahrscheinlichkeitsmassenfunktion zurück. Für unsere Zwecke verwenden wir immer TRUE.

Um diese Funktion auf unser Beispiel anzuwenden, wählen wir eine der vier Zellen in der 2×2-Tabelle zur Verwendung aus. Jede Zelle reicht aus, aber wir verwenden für dieses Beispiel die Zelle oben links mit dem Wert „4“.

Als nächstes geben wir die folgenden Werte für die Funktion ein:

= HYPGEOM.VERT (Wert in einzelner Zelle, Gesamtzahl der Spalten, Gesamtzahl der Zeilen, Gesamtstichprobengröße, WAHR)

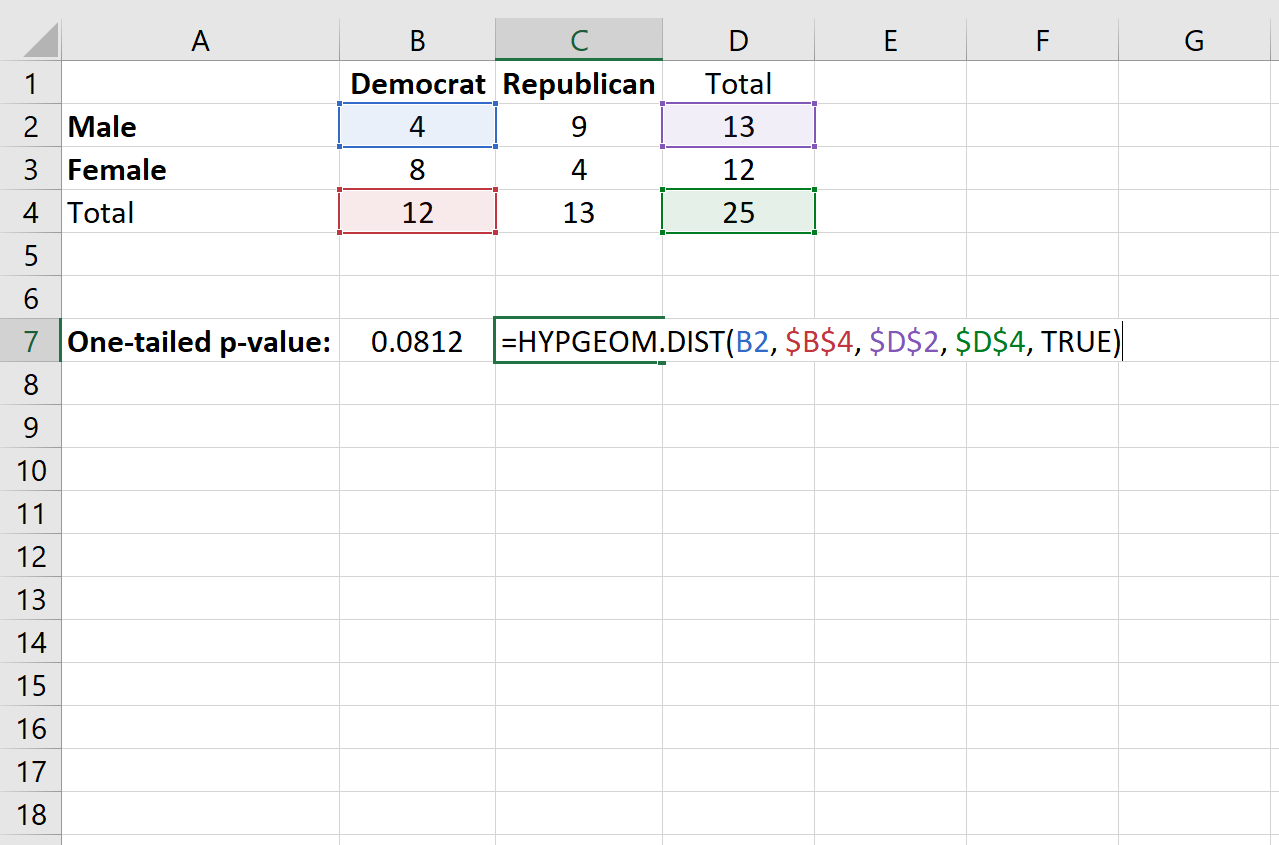
Dies ergibt einen einseitigen p-Wert von 0,0812 .

Um den zweiseitigen p-Wert für den Test zu ermitteln, fügen wir die folgenden zwei Wahrscheinlichkeiten hinzu:

• Die Wahrscheinlichkeit, in der interessierenden Zelle x „Erfolg“ zu erzielen. In unserem Fall ist dies die Wahrscheinlichkeit, 4 Erfolge zu erzielen (wir haben bereits festgestellt, dass diese Wahrscheinlichkeit 0,0812 beträgt).
• 1 – die Wahrscheinlichkeit, (Gesamtzahl der Spalten – x „Erfolg“) in die interessierende Zelle zu gelangen. In diesem Fall beträgt die Gesamtzahl der Spalten für „Demokrat“ 12, wir finden also 1 – (Wahrscheinlichkeit von 8 „Erfolg“).

Hier ist die Formel, die wir verwenden werden:

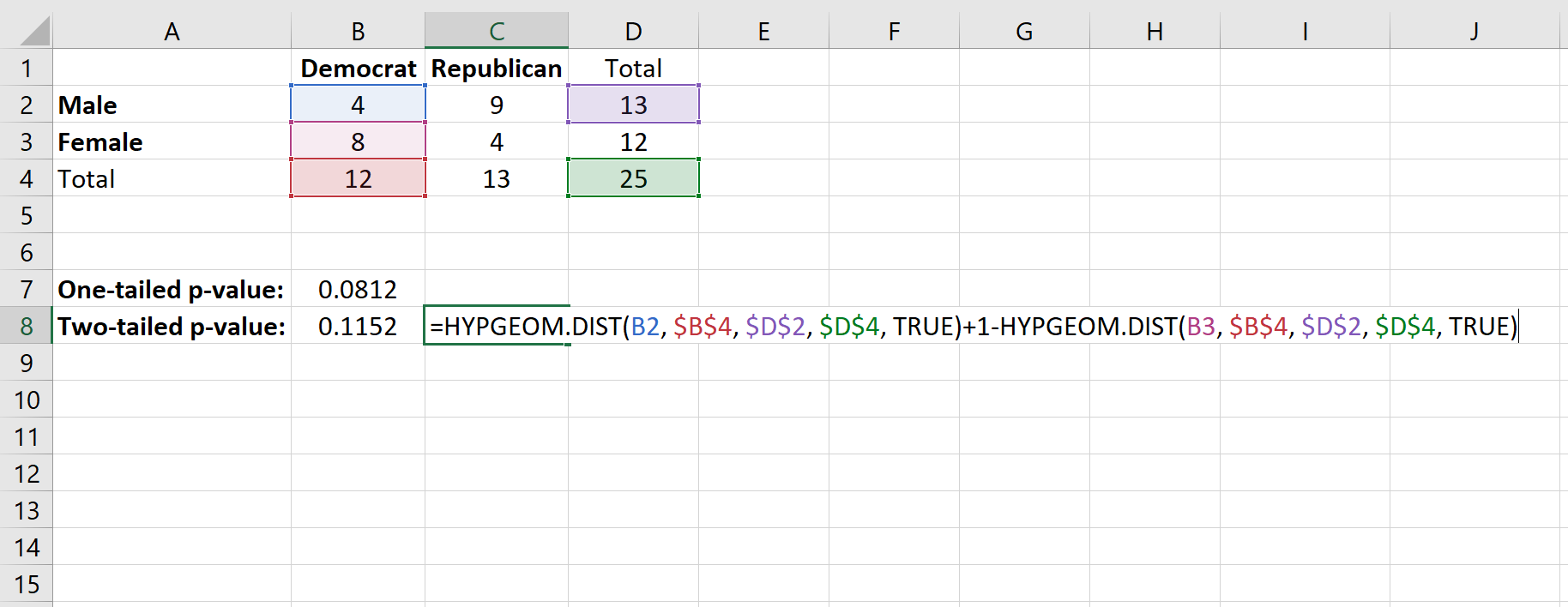
Dies ergibt einen zweiseitigen p-Wert von 0,1152 .

In beiden Fällen, unabhängig davon, ob wir einen einseitigen oder zweiseitigen Test durchführen, beträgt der p-Wert nicht weniger als 0,05, sodass wir die Nullhypothese nicht ablehnen können. Mit anderen Worten: Wir haben keine ausreichenden Belege dafür, dass ein signifikanter Zusammenhang zwischen Geschlecht und politischen Parteipräferenzen besteht.

Zusätzliche Ressourcen

So führen Sie einen Chi-Quadrat-Unabhängigkeitstest in Excel durch
So führen Sie einen Chi-Quadrat-Fit-Test in Excel durch
So berechnen Sie Cramers V in Excel