So verwenden sie geometpdf() und geometcdf() auf einem ti-84-rechner

Die geometrische Verteilung beschreibt die Wahrscheinlichkeit, in einer Versuchsreihe mit folgenden Merkmalen eine bestimmte Anzahl von Fehlschlägen zu erleben, bevor der erste Erfolg eintritt:

• Es gibt nur zwei mögliche Ergebnisse: Erfolg oder Misserfolg.
• Die Erfolgswahrscheinlichkeit ist bei jedem Versuch gleich.

Folgt eine Zufallsvariable

P(X=k) = (1-p) ^kp

Gold:

• k: Anzahl der Misserfolge vor dem ersten Erfolg
• p: Erfolgswahrscheinlichkeit bei jedem Versuch

Die kumulative Wahrscheinlichkeit , dass wir bis zum ersten Erfolg k oder weniger Ausfälle erleben, kann mithilfe der folgenden Formel ermittelt werden:

P(X≤k) = 1 – (1-p) ^k+1

Um die mit der geometrischen Verteilung verknüpften Wahrscheinlichkeiten auf einem TI-84-Rechner zu berechnen, können Sie die folgenden Funktionen verwenden:

• geometpdf (Wahrscheinlichkeiten, Tests)
• geometcdf(Wahrscheinlichkeit, Tests)

Die folgenden Beispiele zeigen, wie Sie jede dieser Funktionen in der Praxis nutzen können.

Beispiel 1: Verwendung von geometpdf()

Angenommen, ein Forscher wartet vor einer Bibliothek, um die Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Wie groß ist die Wahrscheinlichkeit, dass die vierte Person, mit der der Forscher spricht, als erste das Gesetz unterstützt?

Um diese Frage zu beantworten, können wir die Funktion geometpdf() verwenden.

Drücken Sie 2nd und dann VARS . Scrollen Sie zu geometpdf() und drücken Sie ENTER .

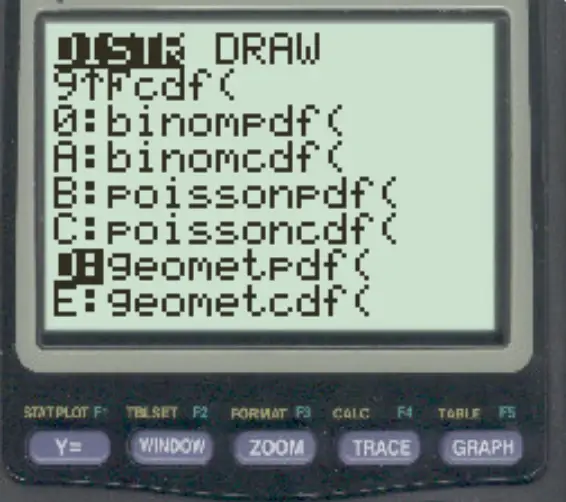
Geben Sie dann die folgenden Werte ein und drücken Sie die EINGABETASTE .

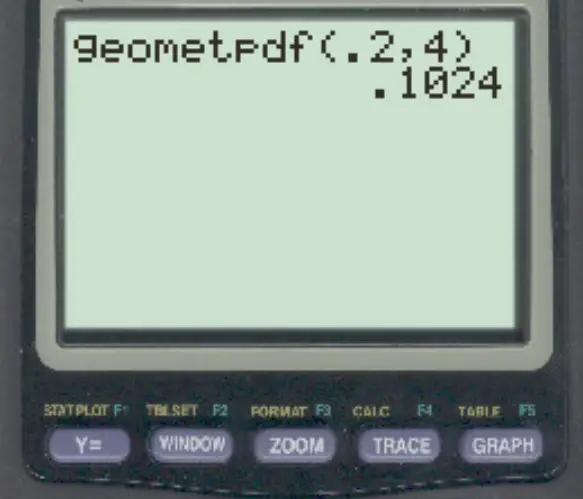
Die Wahrscheinlichkeit, dass die vierte Person, mit der der Forscher spricht, als erste das Gesetz unterstützt, beträgt 0,1024 .

Beispiel 2: Verwendung von geometcdf()

Nehmen wir an, wir wissen, dass 4 % der Menschen, die einen bestimmten Banker aufsuchen, dies tun, um Insolvenz anzumelden. Wie groß ist die Wahrscheinlichkeit, dass der Bankier weniger als 9 Personen trifft, bevor er jemanden trifft, der Insolvenz anmeldet?

Um diese Frage zu beantworten, können wir die Funktion geometcdf() verwenden.

Drücken Sie 2nd und dann VARS . Scrollen Sie nach unten zu geometcdf() und drücken Sie ENTER .

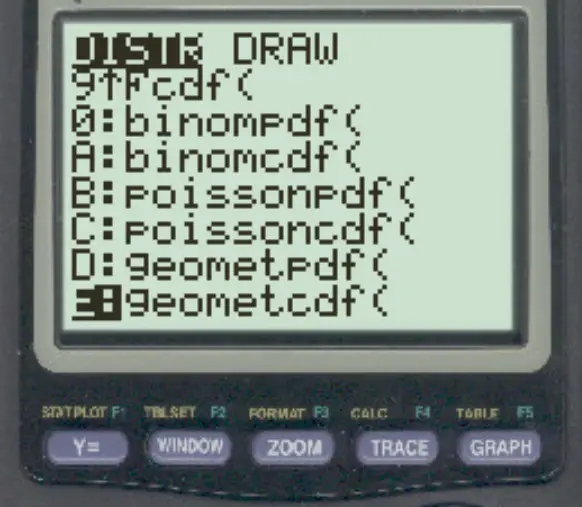
Geben Sie dann die folgenden Werte ein und drücken Sie die EINGABETASTE .

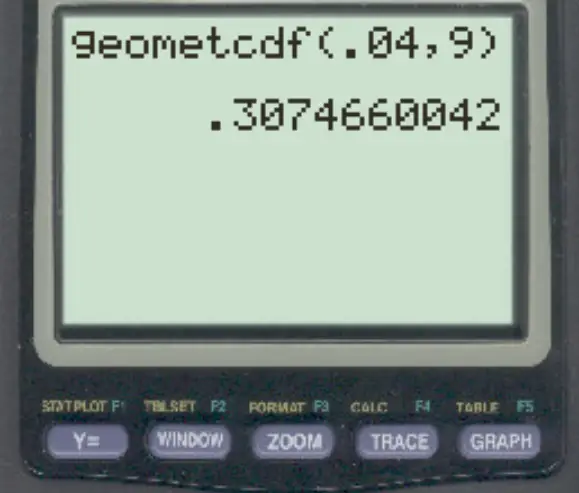
Die Wahrscheinlichkeit, dass der Bankier weniger als 9 Personen trifft, bevor er jemanden trifft, der Insolvenz anmeldet, beträgt 0,307466 .

Bonus: Fühlen Sie sich frei, diesen Online-Rechner für die geometrische Verteilung zu verwenden, um Ihre Ergebnisse zu bestätigen.

Zusätzliche Ressourcen

So berechnen Sie Normalwahrscheinlichkeiten mit einem TI-84-Rechner
So berechnen Sie Binomialwahrscheinlichkeiten mit einem TI-84-Rechner
So berechnen Sie Poisson-Wahrscheinlichkeiten mit einem TI-84-Rechner