Eine einführung in die geometrische verteilung

Die geometrische Verteilung beschreibt die Wahrscheinlichkeit, in einer Reihe von Bernoulli-Versuchen eine bestimmte Anzahl von Fehlschlägen zu erleben, bevor der erste Erfolg eintritt.

Ein Bernoulli-Versuch ist ein Experiment mit nur zwei möglichen Ergebnissen – „Erfolg“ oder „Misserfolg“ – und die Erfolgswahrscheinlichkeit ist bei jeder Durchführung des Experiments gleich.

Ein Beispiel für einen Bernoulli-Aufsatz ist ein Münzwurf. Die Münze kann nur auf zwei Köpfen landen (wir könnten Kopf als „Treffer“ und Zahl als „Misserfolg“ bezeichnen) und die Erfolgswahrscheinlichkeit bei jedem Wurf beträgt 0,5, vorausgesetzt, die Münze ist fair.

Folgt eine Zufallsvariable

P(X=k) = (1-p) ^kp

Gold:

• k: Anzahl der Misserfolge vor dem ersten Erfolg
• p: Erfolgswahrscheinlichkeit bei jedem Versuch

Nehmen wir zum Beispiel an, wir möchten wissen, wie oft wir eine faire Münze werfen müssen, bis sie Kopf zeigt. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit von 0, 1, 2, 3 Ausfällen usw. zu bestimmen. bevor die Münze auf „Kopf“ landet:

Hinweis: Die Münze kann 0 „Misserfolg“ erleiden, wenn sie beim ersten Wurf „Kopf“ ergibt.

P(X=0) = (1-.5) ⁰ (.5) = 0,5

P(X=1) = (1-.5) ¹ (.5) = 0,25

P(X=2) = (1-.5) ² (.5) = 0,125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Wir können die Wahrscheinlichkeit beliebig vieler Münzwürfe bis ins Unendliche berechnen. Anschließend erstellen wir ein einfaches Histogramm, um diese Wahrscheinlichkeitsverteilung zu visualisieren:

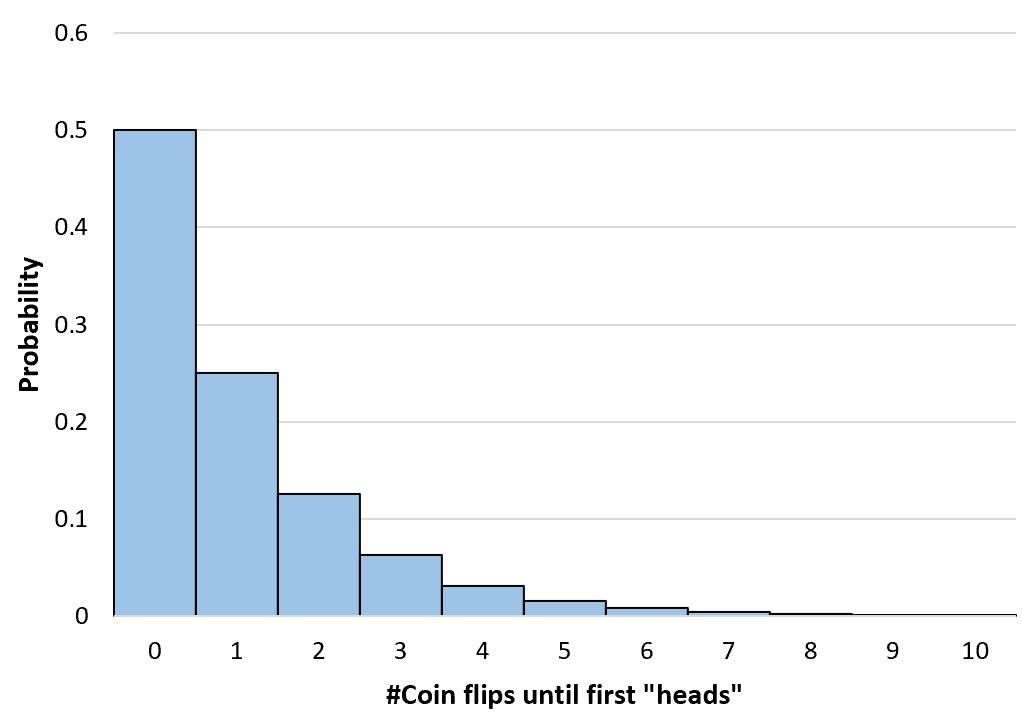
Berechnung kumulativer geometrischer Wahrscheinlichkeiten

Die kumulative Wahrscheinlichkeit , dass wir bis zum ersten Erfolg k oder weniger Ausfälle erleben, kann durch die folgende Formel ermittelt werden:

P(X≤k) = 1 – (1-p) ^k+1

Gold:

• k: Anzahl der Misserfolge vor dem ersten Erfolg
• p: Erfolgswahrscheinlichkeit bei jedem Versuch

Nehmen wir zum Beispiel an, wir möchten die Wahrscheinlichkeit wissen, dass es drei oder weniger „Fehltreffer“ braucht, bis die Münze schließlich auf dem Kopf landet. Zur Berechnung dieser Wahrscheinlichkeit würden wir die folgende Formel verwenden:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Wir können jede kumulative Wahrscheinlichkeit mit einer ähnlichen Formel berechnen:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0,5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Wir können diese kumulativen Wahrscheinlichkeiten für beliebig viele Münzwürfe bis hin zur Unendlichen berechnen. Anschließend können wir ein Histogramm erstellen, um diese kumulative Wahrscheinlichkeitsverteilung zu visualisieren:

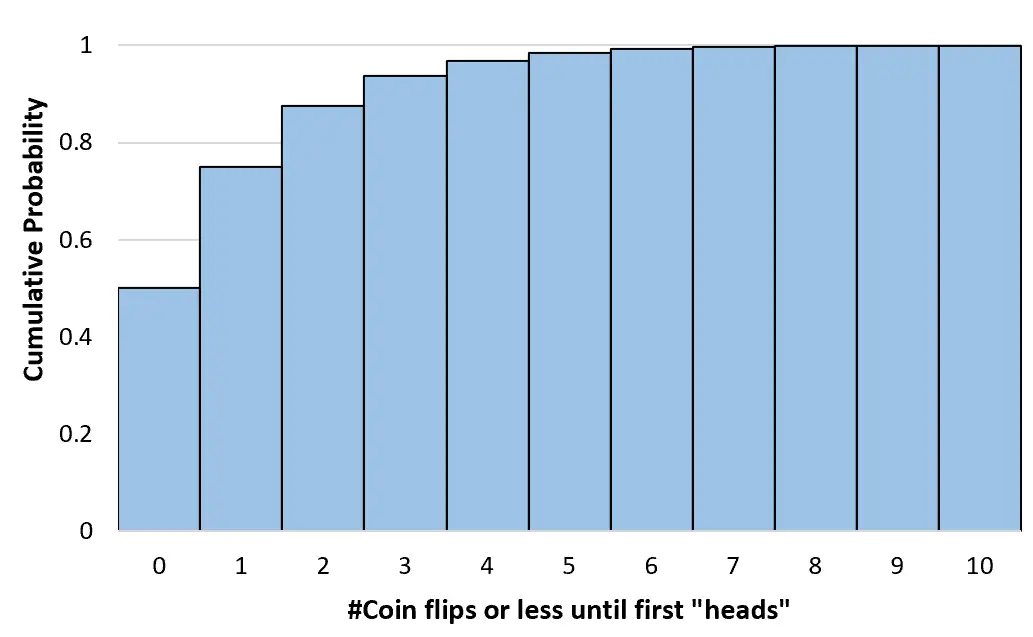
Eigenschaften der geometrischen Verteilung

Die geometrische Verteilung hat folgende Eigenschaften:

Der Mittelwert der Verteilung beträgt (1-p) / p .

Die Varianz der Verteilung beträgt (1-p) / p ² .

Zum Beispiel:

Die durchschnittliche Häufigkeit, mit der wir erwarten, dass eine Münze „Kopf“ landet, bevor sie „Zahl“ landet, wäre (1-p) / p = (1-.5) / .5 = 1 .

Die Varianz der Anzahl der Würfe bis zum Ergebnis „Kopf“ wäre (1-p)/ ^p2 =(1-.5)/. ⁵² = 2 .

Probleme der geometrischen Verteilungspraxis

Verwenden Sie die folgenden Übungsaufgaben, um Ihr Wissen über geometrische Verteilung zu testen.

Hinweis: Wir verwenden den Rechner für die geometrische Verteilung , um die Antworten auf diese Fragen zu berechnen.

Problem 1

Frage: Ein Forscher wartet vor einer Bibliothek, um die Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Wie groß ist die Wahrscheinlichkeit, dass die vierte Person, mit der der Forscher spricht, als erste das Gesetz unterstützt?

Antwort: Die Anzahl der „Misserfolge“ bis zum ersten Erfolg – also die Anzahl der Menschen, die das Gesetz nicht unterstützen, bis die erste Person es unterstützt – beträgt 3. Also bei Verwendung des geometrischen Verteilungsrechners mit p = 0,2 und x = 3 Ausfälle, wir finden, dass P(X=3) = 0,10240 .

Problem 2

Frage: Ein Forscher wartet vor einer Bibliothek, um die Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Wie groß ist die Wahrscheinlichkeit, dass der Forscher mit mehr als vier Personen sprechen müsste, um jemanden zu finden, der das Gesetz unterstützt?

Antwort: Unter Verwendung des geometrischen Verteilungsrechners mit p = 0,2 und x = 4 Ausfällen finden wir, dass P(X>4) = 0,32768 ist.

Problem 3

Frage: Ein Forscher wartet vor einer Bibliothek, um die Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Mit wie vielen Personen muss die Forscherin voraussichtlich sprechen, bis sie jemanden findet, der das Gesetz unterstützt?

Antwort: Denken Sie daran, dass der Mittelwert der geometrischen Verteilung (1-p) / p beträgt. In dieser Situation wäre der Durchschnitt (1-.2) / .2 = 4 .