So verwenden sie die geometrische verteilung in excel

Die geometrische Verteilung beschreibt die Wahrscheinlichkeit, in einer Reihe von Bernoulli-Versuchen eine bestimmte Anzahl von Fehlschlägen zu erleben, bevor der erste Erfolg eintritt.

Ein Bernoulli-Versuch ist ein Experiment mit nur zwei möglichen Ergebnissen – „Erfolg“ oder „Misserfolg“ – und die Erfolgswahrscheinlichkeit ist bei jeder Durchführung des Experiments gleich.

Ein Beispiel für einen Bernoulli-Aufsatz ist ein Münzwurf. Die Münze kann nur auf zwei Köpfen landen (wir könnten Kopf als „Treffer“ und Zahl als „Misserfolg“ bezeichnen) und die Erfolgswahrscheinlichkeit bei jedem Wurf beträgt 0,5, vorausgesetzt, die Münze ist fair.

Folgt eine Zufallsvariable

P(X=k) = (1-p) ^kp

Gold:

• k: Anzahl der Misserfolge vor dem ersten Erfolg
• p: Erfolgswahrscheinlichkeit bei jedem Versuch

Die folgenden Beispiele zeigen, wie Wahrscheinlichkeiten im Zusammenhang mit der geometrischen Verteilung in Excel berechnet werden.

Beispiel 1: Wirf eine Münze

Angenommen, wir werfen eine Münze und möchten die Wahrscheinlichkeit wissen, dass es genau drei „Fehlschläge“ dauert, bis eine Münze schließlich „Kopf“ landet.

Zur Berechnung dieser Wahrscheinlichkeit würden wir die folgende Formel verwenden:

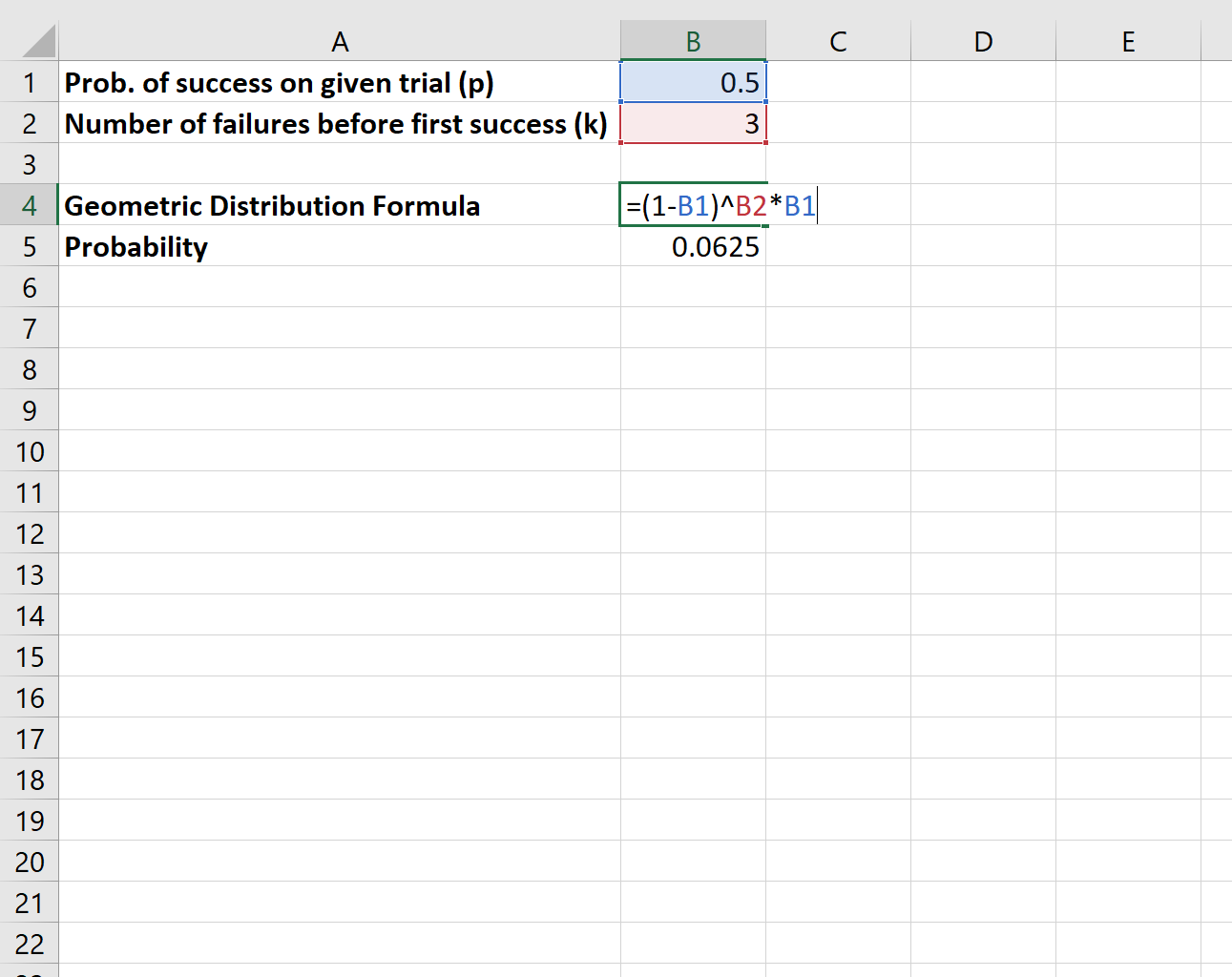
Die Wahrscheinlichkeit, dass wir dreimal „fehlschlagen“, bis eine Münze schließlich „Kopf“ zeigt, beträgt 0,0625 .

Beispiel 2: Freiwurfschießen

Angenommen, ein bestimmter Basketballspieler macht 60 % seiner Freiwürfe. Wie groß ist die Wahrscheinlichkeit, dass der Spieler vier Freiwürfe verpasst, bis er schließlich einen macht?

Zur Berechnung dieser Wahrscheinlichkeit würden wir die folgende Formel verwenden:

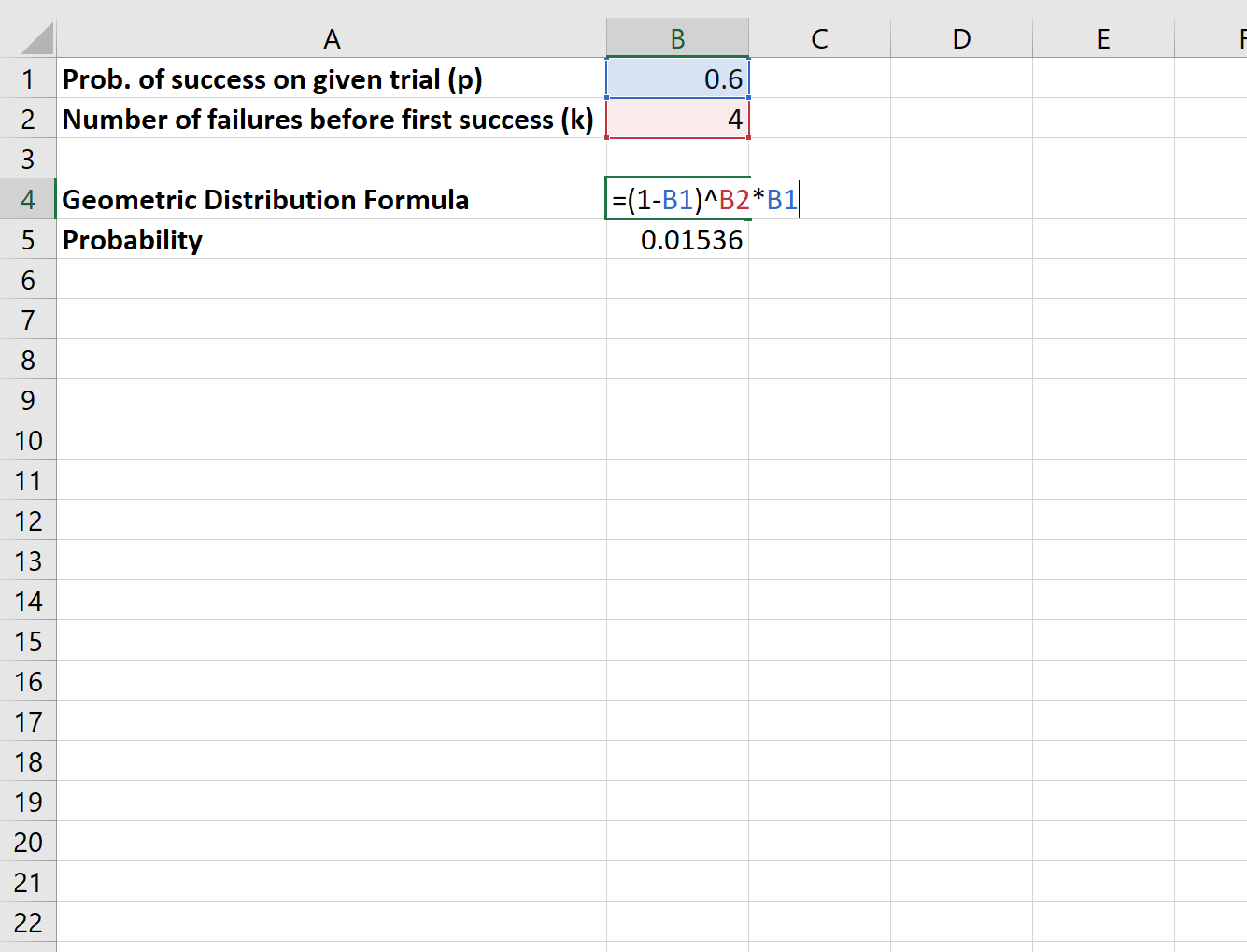
Die Wahrscheinlichkeit, dass der Spieler vier Freiwürfe verpasst, bis er schließlich einen macht, beträgt 0,01536 .

Beispiel 3: Unterstützung eines Gesetzes

Angenommen, ein Forscher wartet vor einer Bibliothek, um die Leute zu fragen, ob sie ein bestimmtes Gesetz unterstützen. Die Wahrscheinlichkeit, dass eine bestimmte Person das Gesetz unterstützt, beträgt p = 0,2. Wie groß ist die Wahrscheinlichkeit, dass die vierte Person, mit der der Forscher spricht, als erste das Gesetz unterstützt?

Zur Berechnung dieser Wahrscheinlichkeit würden wir die folgende Formel verwenden:

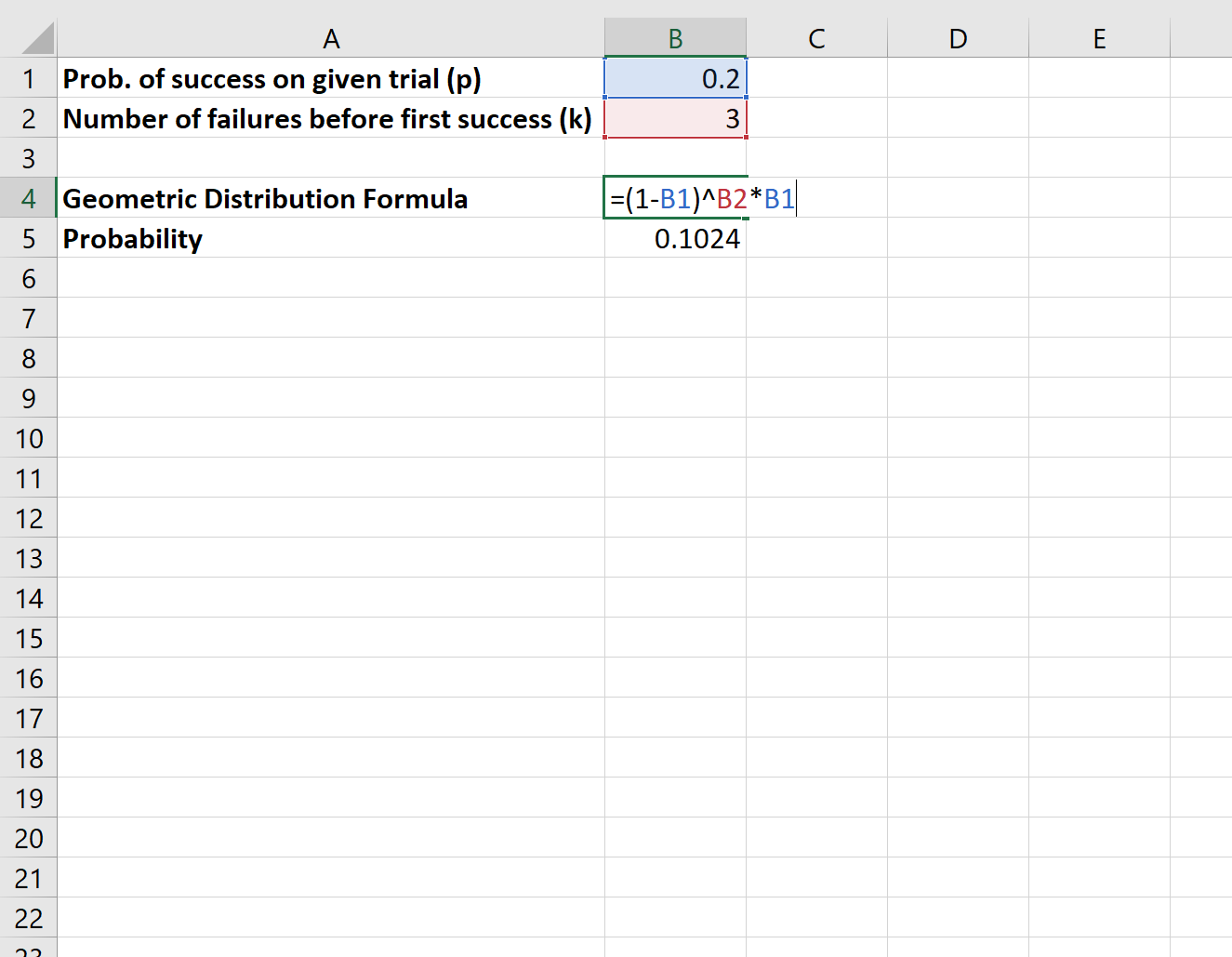
Die Wahrscheinlichkeit, dass die vierte Person, mit der der Forscher spricht, als erste das Gesetz unterstützt, beträgt 0,1024 .

Zusätzliche Ressourcen

Eine Einführung in die geometrische Verteilung
Geometrischer Verteilungsrechner
5 konkrete Beispiele für geometrische Verteilung