Geometrische mittel

Von Dr. Benjamin Anderson August 6, 2023 Statistiken Keine Kommentare

In diesem Artikel erklären wir, was das geometrische Mittel ist, wie es berechnet wird und was der Unterschied zwischen dem geometrischen Mittel und dem arithmetischen Mittel ist. Sie können sich auch eine Schritt-für-Schritt-Anleitung zum geometrischen Mittelwert ansehen und erfahren, welche Eigenschaften dieser Mittelwerttyp hat. Schließlich finden Sie einen Rechner, mit dem Sie das geometrische Mittel eines beliebigen Datensatzes berechnen können.

Was ist das geometrische Mittel?

Das geometrische Mittel ist ein Maß für die Zentralität der deskriptiven Statistik. Das geometrische Mittel einer Reihe statistischer Daten ist gleich der n-ten Wurzel des Produkts aller Werte.

Das geometrische Mittel wird in der Unternehmensfinanzierung zur Berechnung von Renditen, prozentualen Durchschnittswerten und Zinseszinsen verwendet.

Die Formel für das geometrische Mittel lautet daher wie folgt:

Der geometrische Mittelwert kann nur berechnet werden, wenn alle Daten in der Stichprobe positiv sind. Denn wenn ein Wert negativ ist, hätte die Wurzel eine negative Lösung oder keine Lösung. Wenn andererseits ein Datenwert Null ist, würde die Multiplikation der Daten Null ergeben und daher wäre das geometrische Mittel gleich 0.

Es gibt nicht nur das geometrische Mittel, sondern auch das arithmetische Mittel, das gewichtete Mittel, das quadratische Mittel und das harmonische Mittel.

Differenz zwischen geometrischem Mittel und arithmetischem Mittel

Der Hauptunterschied zwischen dem geometrischen Mittel und dem arithmetischen Mittel besteht darin, dass das geometrische Mittel weniger empfindlich auf Extremwerte reagiert als das arithmetische Mittel. Darüber hinaus kann das arithmetische Mittel mit negativen und Nullwerten berechnet werden, während das geometrische Mittel nur mit positiven Werten berechnet werden kann.

Ebenso wird das geometrische Mittel im Allgemeinen niedriger sein als das arithmetische Mittel für denselben Datensatz.

Es ist auch zu beachten, dass die Berechnung des geometrischen Mittels komplexer ist und daher seine statistische Aussagekraft schwieriger zu interpretieren ist.

Kurz gesagt, der geometrische Durchschnitt hat im Vergleich zum arithmetischen Durchschnitt Vor- und Nachteile und je nach Art der Daten ist es angebracht, diesen oder jenen Durchschnitt zu berechnen.

So berechnen Sie das geometrische Mittel

Zur Berechnung des geometrischen Mittels müssen folgende Schritte durchgeführt werden:

Berechnen Sie das Produkt aller statistischen Daten in der Stichprobe.
Finden Sie die n-te Wurzel des berechneten Produkts.
Das erhaltene Ergebnis ist das geometrische Mittel der statistischen Stichprobe.

Wie Sie sehen, ist das Ermitteln des geometrischen Mittelwerts eines Datensatzes mit einem Taschenrechner oder Computerprogramm relativ einfach, da Sie lediglich ein Produkt und eine Wurzel berechnen müssen. Im Gegenteil, die Berechnung per Hand ist recht mühsam.

👉 Aus diesem Grund empfehlen wir, den untenstehenden Rechner zu verwenden, um das geometrische Mittel eines Datensatzes zu berechnen.

Beispiel für einen geometrischen Mittelwert

Sobald wir die Theorie über den geometrischen Mittelwert kennengelernt haben, erstellen wir ein Beispiel, damit Sie genau sehen können, wie Sie den geometrischen Mittelwert ermitteln.

Die wirtschaftlichen Ergebnisse eines Unternehmens in den letzten fünf Jahren sind bekannt. Im ersten Jahr erwirtschaftete das Unternehmen eine wirtschaftliche Rentabilität von 10 %, im zweiten Jahr erreichte der Gewinn 23 %, im dritten Jahr betrug der verdiente Gelder 16 %, im vierten Jahr erreichte es eine wirtschaftliche Rentabilität von 7 % und die Investition im fünften Jahr eine Rendite von 20 %. Sie werden gebeten, den Durchschnitt aller Prozentsätze zu berechnen.

Wie wir gesehen haben, sollten Sie zur Berechnung des Durchschnitts der Prozentsätze nicht den arithmetischen Durchschnitt verwenden, sondern die Berechnung mit dem geometrischen Durchschnitt durchführen.

Daher wenden wir die geometrische Mittelformel an:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

Und wir setzen die Beispielwerte in die Formel ein und führen die Berechnung durch:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Beachten Sie, dass wir fünf Datenpunkte haben und daher die fünfte Wurzel berechnen.

Das numerische Ergebnis des geometrischen Mittels beträgt 1,15, was bedeutet, dass das Unternehmen jedes Jahr ein Wirtschaftswachstum von durchschnittlich 15 % verzeichnete.

Bedenken Sie, dass wir den geometrischen Mittelwert ermitteln konnten, weil alle Werte positiv waren, aber wenn irgendein Prozentsatz negativ gewesen wäre, hätten wir die Daten als positive Dezimalzahl mit dem ganzzahligen Teil in die Formel einfügen müssen. gleich Null. Beispielsweise sollte ein Wachstum von -30 % in der Formel als 0,70 (1-0,3=0,7) ausgedrückt werden.

Geometrischer Mittelrechner

Geben Sie eine beliebige Beispielstatistik in den Rechner unten ein, um den geometrischen Mittelwert zu ermitteln. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden. Denken Sie daran, dass Sie den geometrischen Mittelwert nicht bestimmen können, wenn ein Wert negativ oder Null ist.

Eigenschaften des geometrischen Mittels

Das geometrische Mittel weist folgende Eigenschaften auf:

Dies ist eine Durchschnittsart, die sehr nützlich ist, um den Durchschnitt von Prozentsätzen oder Indizes zu ermitteln.

Sie kann nur berechnet werden, wenn alle Daten positiv sind.

Die geometrische Bedeutung des geometrischen Mittels zweier Zahlen a und b ist die Seite eines Quadrats mit der gleichen Fläche wie das Rechteck, dessen Seiten a und b messen.

$MG(a,b)=\sqrt{a\cdot b}$

Die geometrische Bedeutung des geometrischen Mittels der drei Zahlen a , b und c ist die Seite eines Würfels, dessen Volumen dem Parallelepiped der Seiten a , b und c entspricht.

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Der Logarithmus des geometrischen Mittels eines Datensatzes ergibt das arithmetische Mittel der Logarithmen desselben Satzes.

Das geometrische Mittel einer Wertemenge ist immer kleiner oder gleich dem arithmetischen Mittel.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Der gewichtete geometrische Mittelwert wird auf die gleiche Weise wie der geometrische Mittelwert berechnet, jedoch durch Addition von Gewichtungen zum Exponenten jedes Datenelements, um die statistischen Werte zu gewichten.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

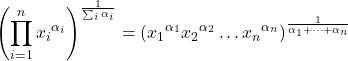
Berechnen Sie den geometrischen Mittelwert in Excel

Lassen Sie uns abschließend sehen, wie Sie mit dem Excel-Programm das geometrische Mittel eines Datensatzes ermitteln.

Um den geometrischen Mittelwert in Excel zu berechnen, müssen Sie die Funktion MEANS.GEOM verwenden. Geben Sie einfach alle Werte ein, deren geometrischer Mittelwert Sie ermitteln möchten, und die Funktion gibt das Ergebnis des geometrischen Mittelwerts zurück.

Um beispielsweise das geometrische Mittel des oben bearbeiteten Beispiels zu bestimmen, müssen Sie in ein Excel-Feld =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) schreiben.

Beachten Sie, dass die Funktion einen Fehler zurückgibt, wenn einer der Werte Null oder negativ ist.

Wie Sie sehen, ist die Berechnung eines geometrischen Mittelwerts mit Excel viel einfacher und schneller, da Sie lediglich die Daten auf ein Blatt kopieren und eine Formel verwenden müssen.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen