Die drei hypothesen wurden in einem gepaarten t-test formuliert

Ein t-Test für gepaarte Stichproben wird verwendet, um die Mittelwerte zweier Stichproben zu vergleichen, wenn jede Beobachtung in einer Stichprobe mit einer Beobachtung in der anderen Stichprobe verknüpft werden kann.

Diese Art von Test geht von den folgenden Annahmen über die Daten aus:

1. Unabhängigkeit: Jede Beobachtung muss unabhängig von jeder anderen Beobachtung sein.

2. Normalität: Die Unterschiede zwischen Paaren sollten annähernd normalverteilt sein.

3. Keine extremen Ausreißer: Es sollte keine extremen Ausreißer in den Unterschieden geben.

Wenn eine oder mehrere dieser Annahmen nicht erfüllt sind, können die Ergebnisse des T-Tests für gepaarte Stichproben unzuverlässig oder irreführend sein.

In diesem Tutorial erklären wir jede Annahme, wie man ermittelt, ob die Annahme erfüllt ist, und was zu tun ist, wenn sie verletzt wird.

Hypothese 1: Unabhängigkeit

Bei einem T-Test für gepaarte Stichproben wird davon ausgegangen, dass jede Beobachtung unabhängig von allen anderen Beobachtungen ist.

So überprüfen Sie diese Hypothese

Der einfachste Weg, diese Annahme zu überprüfen, besteht darin, zu überprüfen, ob jede Beobachtung mithilfe einer Zufallsstichprobenmethode erfasst wurde.

Wenn eine Zufallsstichprobenmethode verwendet wurde (z. B. eine einfache Zufallsstichprobe), können wir davon ausgehen, dass jede Beobachtung unabhängig von allen anderen Beobachtungen ist.

Was tun, wenn diese Annahme nicht respektiert wird?

Wenn diese Annahme nicht erfüllt ist, sind die Ergebnisse des T-Tests für gepaarte Stichproben völlig ungültig.

In diesem Szenario ist es am besten, neue Beobachtungen mithilfe einer Zufallsstichprobenmethode zu sammeln, um sicherzustellen, dass jede Beobachtung unabhängig ist.

Hypothese 2: Normalität

Bei einem T-Test für gepaarte Stichproben wird davon ausgegangen, dass die Unterschiede zwischen Paaren annähernd normalverteilt sein sollten.

Dies ist eine entscheidende Annahme, denn wenn die Unterschiede zwischen Paaren nicht normalverteilt sind, ist es nicht zulässig, den p-Wert des Tests zu verwenden, um Schlussfolgerungen zu ziehen.

So überprüfen Sie diese Hypothese

Der einfachste Weg, diese Hypothese zu testen, besteht darin, einfach ein Histogramm der gepaarten Differenzen zu erstellen und visuell zu überprüfen, ob das Histogramm eine Glockenform hat oder nicht.

Wenn das Histogramm beispielsweise so aussieht, würden wir sagen, dass die Normalitätsannahme erfüllt ist:

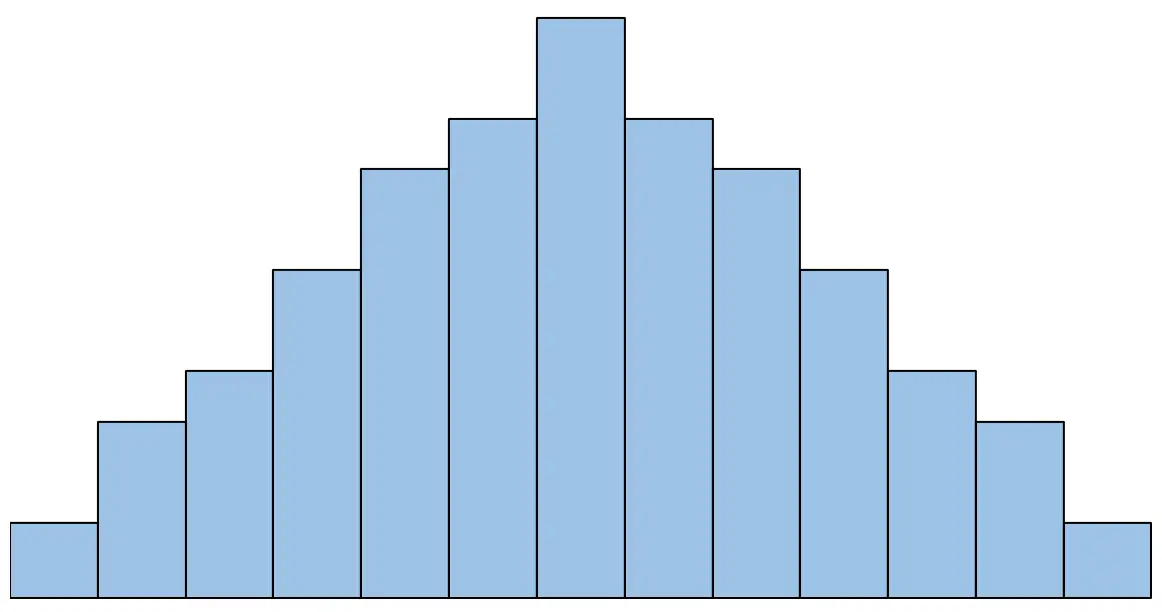
Wenn das Histogramm jedoch so aussieht, würden wir sagen, dass die Normalitätsannahme nicht erfüllt ist:

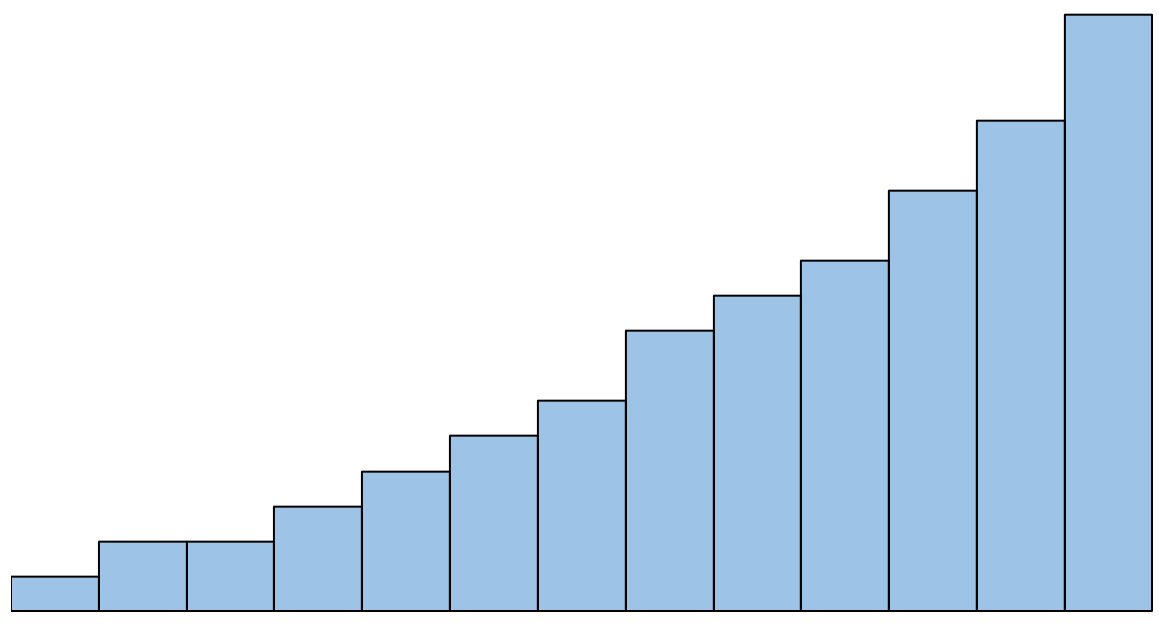
Was tun, wenn diese Annahme nicht respektiert wird?

Wenn diese Annahme verletzt wird, können wir einen Wilcoxon-Signed-Rank-Test durchführen, der als nichtparametrisches Äquivalent des t-Tests für gepaarte Stichproben gilt und nicht davon ausgeht, dass die gepaarten Differenzen normalverteilt sind.

Hypothese 3: keine extremen Ausreißer

Bei einem T-Test für gepaarte Stichproben wird davon ausgegangen, dass die Daten keine extremen Ausreißer enthalten.

So überprüfen Sie diese Hypothese

Der einfachste Weg, diese Hypothese zu testen, besteht darin, ein Boxdiagramm gepaarter Differenzen zu erstellen und visuell zu überprüfen, ob Ausreißer vorhanden sind.

Angenommen, das Boxdiagramm der gepaarten Differenzen sieht beispielsweise so aus:

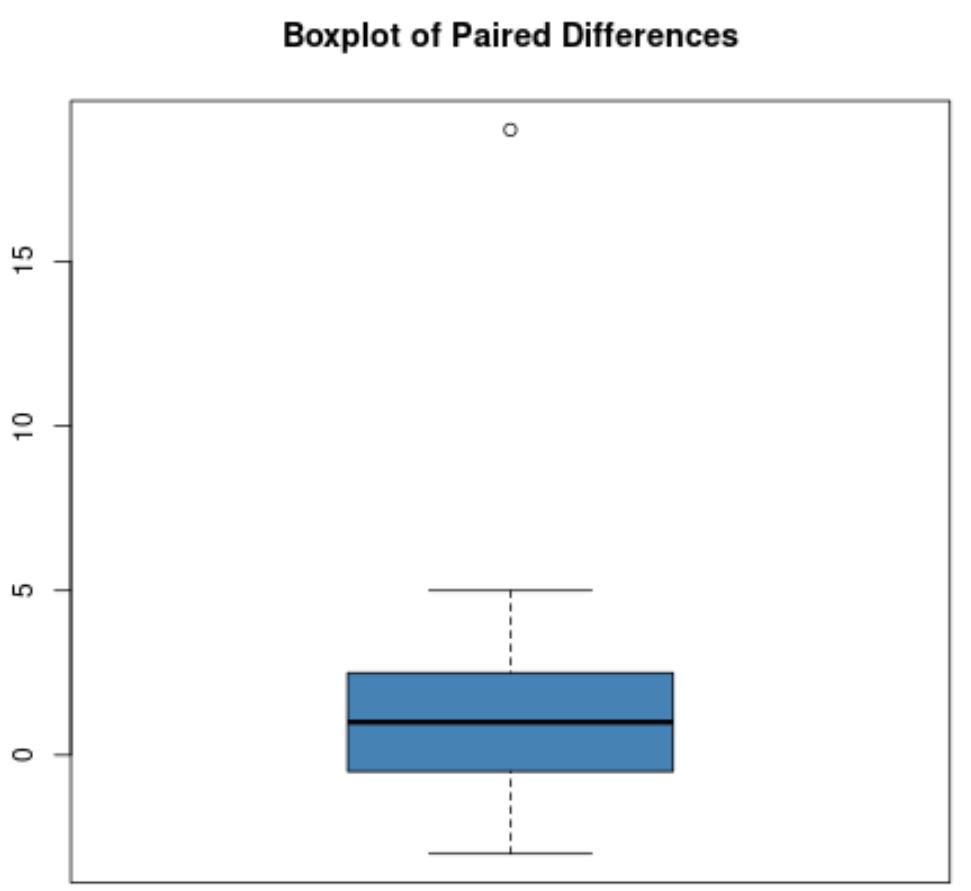
Die meisten gepaarten Differenzen liegen nahe bei Null, es gibt jedoch eine gepaarte Differenz von etwa 19, was eindeutig ein Ausreißer ist.

Hinweis : In einem Boxplot wird normalerweise ein Kreis verwendet, um einen Ausreißer anzuzeigen.

Nehmen wir jedoch an, dass das Boxplot der gepaarten Differenzen wie folgt aussieht:

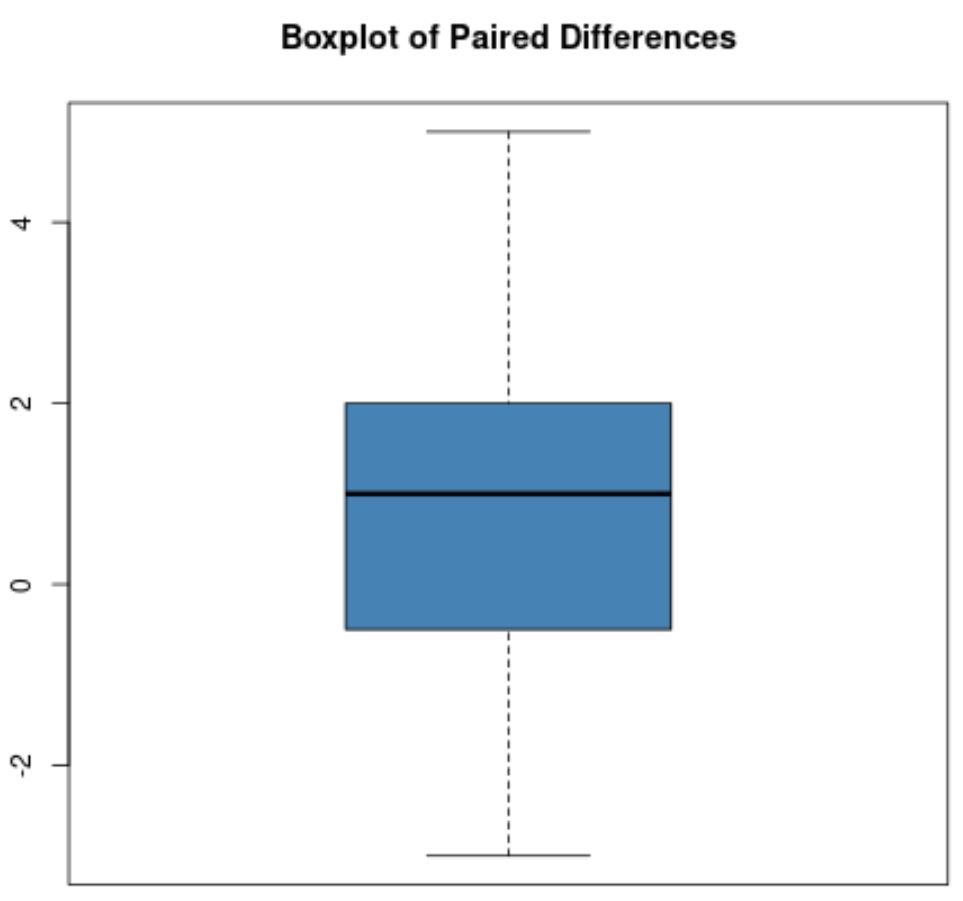
Da es in diesem Boxplot keine eindeutigen Ausreißer gibt, gehen wir davon aus, dass die Daten keine extremen Ausreißer enthalten.

Was tun, wenn diese Annahme nicht respektiert wird?

Wenn diese Annahme verletzt wird, könnten die Ergebnisse des T-Tests für gepaarte Stichproben durch den Ausreißer ungewöhnlich beeinflusst werden.

In diesem Szenario können Sie den Ausreißer entfernen, wenn Sie glauben, dass er einen fehlerhaften Datenpunkt darstellt oder das Ergebnis eines Dateneingabefehlers ist.

Alternativ können Sie den Ausreißer behalten und ihn einfach notieren, wenn Sie die Ergebnisse des T-Tests für gepaarte Stichproben melden.

Zusätzliche Ressourcen

In den folgenden Tutorials werden Annahmen erläutert, die in anderen statistischen Tests getroffen wurden:

Die vier in einem t-Test formulierten Hypothesen
Die vier Hypothesen eines Chi-Quadrat-Tests
Die vier Hypothesen parametrischer Tests