So führen sie einen t-test für gepaarte stichproben in sas durch

Ein t-Test für gepaarte Stichproben wird verwendet, um die Mittelwerte zweier Stichproben zu vergleichen, wenn jede Beobachtung in einer Stichprobe mit einer Beobachtung in der anderen Stichprobe verknüpft werden kann.

In diesem Tutorial wird erläutert, wie Sie einen T-Test für gepaarte Stichproben in SAS durchführen.

Beispiel: T-Test für gepaarte Stichproben in SAS

Angenommen, ein Professor möchte feststellen, ob ein bestimmter Lehrplan Auswirkungen auf die Testergebnisse hat. Um dies zu testen, wählt er nach dem Zufallsprinzip 15 Schüler aus, die einen Vortest absolvieren. Dann lässt er jeden Schüler einen Monat lang den Lehrplan anwenden und anschließend einen Nachtest mit ähnlichem Schwierigkeitsgrad absolvieren.

Die Testergebnisse für jeden der 15 Studenten sind unten aufgeführt:

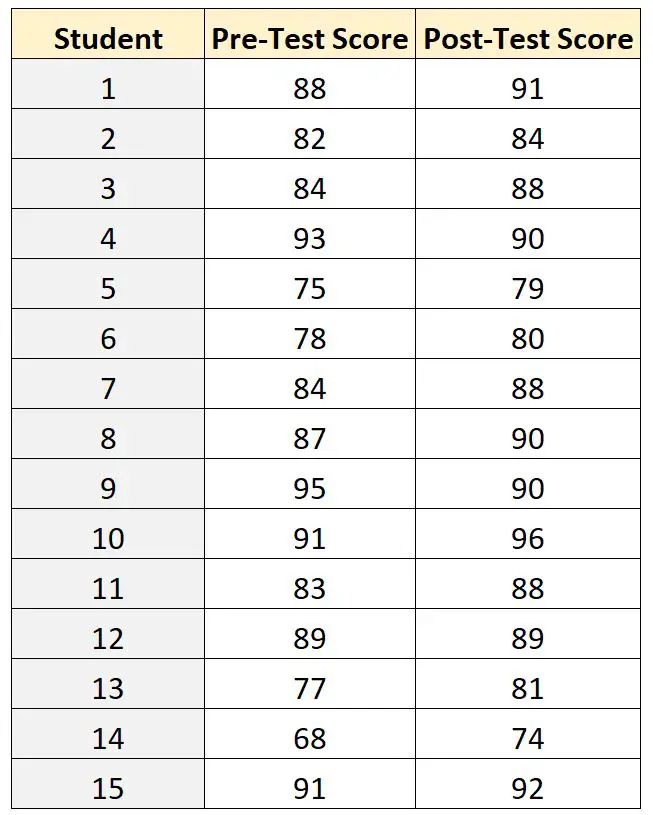
Um die Differenz zwischen den durchschnittlichen Ergebnissen vor und nach dem Test zu vergleichen, kann der Lehrer gepaarte T-Test-Stichproben verwenden, da für jeden Schüler sein Ergebnis vor dem Test mit seinem Ergebnis nach dem Test verknüpft werden kann.

Befolgen Sie die folgenden Schritte, um diesen T-Test für gepaarte Stichproben in SAS durchzuführen:

Schritt 1: Erstellen Sie die Daten

Lassen Sie uns zunächst den folgenden Code verwenden, um den Datensatz in SAS zu erstellen:

 /*create dataset*/
datatest_scores ;
    input pre post;
    datalines ;
88 91
82 84
84 88
93 90
75 79
78 80
84 88
87 90
95 90
91 96
83 88
89 89
77 81
68 74
91 92
;
run ;

/*view dataset*/
proc print data =test_scores;

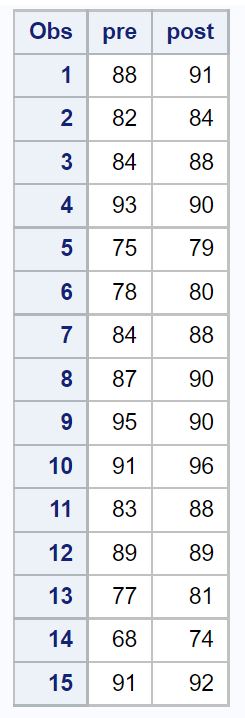
Schritt 2: Führen Sie den T-Test für gepaarte Stichproben durch

Als nächstes können wir proc ttest verwenden, um den T-Test für gepaarte Stichproben durchzuführen:

 /*perform paired samples t-test*/
proc ttest data =test_scores alpha = .05 ;
    paired pre*post;
run ; 

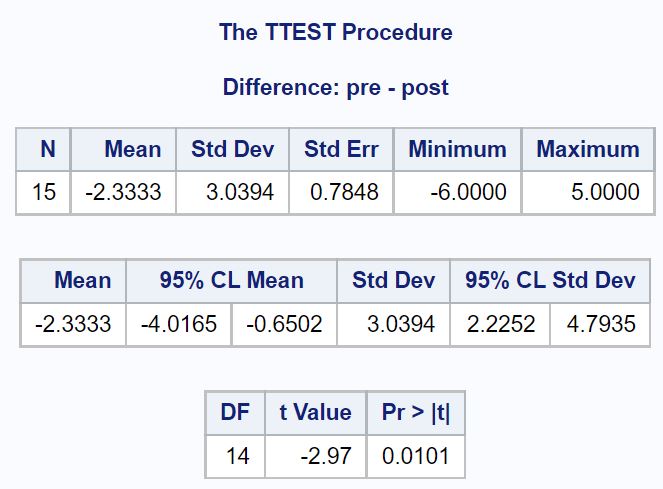
Aus dem Ergebnis können wir Folgendes erkennen:

• Durchschnittliche Differenz zwischen dem Ergebnis vor und nach dem Test: -2,3333
• 95 %-Konfidenzintervall für Mittelwertdifferenz: [-4,0165, -0,6502]

Wir können auch die T-Test-Statistik und den entsprechenden zweiseitigen p-Wert sehen:

• T-Test-Statistik: -2,97
• p-Wert: 0,0101

In diesem Beispiel verwendet der T-Test für gepaarte Stichproben die folgenden Null- und Alternativhypothesen :

• H ₀ : Die durchschnittlichen Ergebnisse vor und nach dem Test sind gleich
• H _A : Die durchschnittlichen Ergebnisse vor und nach dem Test sind nicht gleich

Da der p-Wert ( 0,0101 ) kleiner als 0,05 ist, lehnen wir die Nullhypothese ab.

Das bedeutet, dass wir genügend Beweise haben, um zu sagen, dass die tatsächliche durchschnittliche Testpunktzahl für Studierende vor und nach der Teilnahme am Studienprogramm unterschiedlich ist.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige statistische Tests in SAS durchführen:

So führen Sie einen T-Test bei einer Stichprobe in SAS durch
So führen Sie einen T-Test bei zwei Stichproben in SAS durch
So führen Sie einen Wilcoxon-Signed-Rank-Test in SAS durch