Gepaarter oder ungepaarter t-test: was ist der unterschied?

In der Statistik gibt es zwei Arten von T-Tests bei zwei Stichproben :

Gepaarter T-Test: Wird verwendet, um die Mittelwerte zweier Stichproben zu vergleichen, wenn jedes Individuum in einer Stichprobe auch in der anderen Stichprobe vorkommt.

Ungepaarter T-Test: Wird verwendet, um die Mittelwerte zweier Stichproben zu vergleichen, wenn jedes Individuum in einer Stichprobe unabhängig von jedem Individuum in der anderen Stichprobe ist.

Hinweis: Ein ungepaarter T-Test wird üblicherweise als T-Test für unabhängige Stichproben bezeichnet.

Angenommen, ein Professor möchte feststellen, ob zwei unterschiedliche Lerntechniken zu unterschiedlichen durchschnittlichen Prüfungsergebnissen führen.

Um einen gepaarten T-Test durchzuführen, könnte er 10 Studenten rekrutieren und sie einen Monat lang eine Lerntechnik anwenden lassen und eine Prüfung ablegen, sie dann einen Monat lang die zweite Lerntechnik anwenden lassen und eine weitere Prüfung mit gleichem Schwierigkeitsgrad ablegen.

So würden die Daten aussehen:

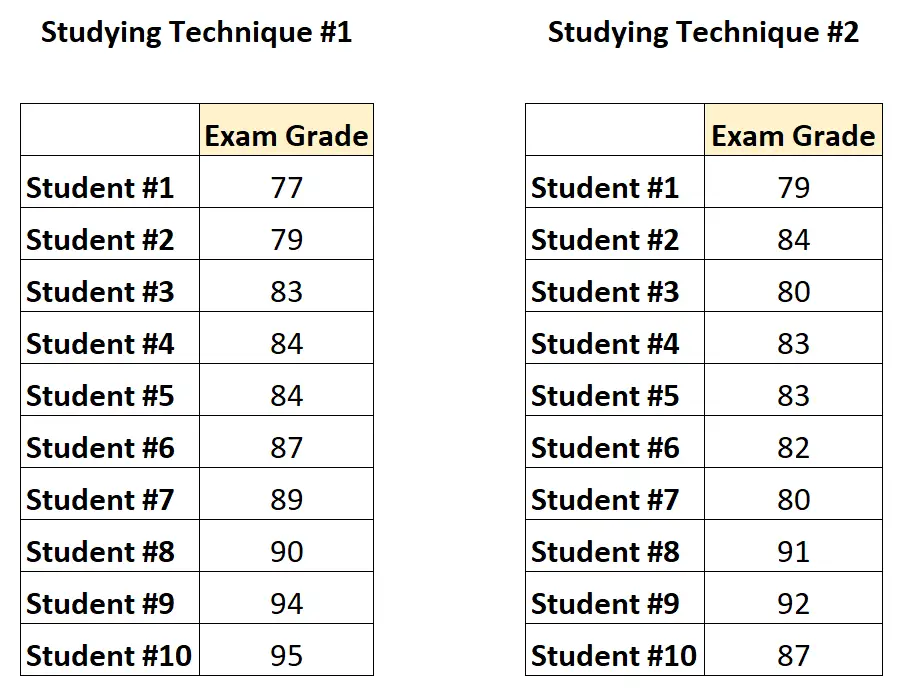
Da jeder Student in jeder Gruppe erscheint, würde der Professor einen gepaarten T-Test durchführen, um festzustellen, ob die durchschnittlichen Ergebnisse zwischen den beiden Gruppen unterschiedlich sind.

Um einen ungepaarten T-Test durchzuführen, könnte er insgesamt 20 Studenten rekrutieren und sie nach dem Zufallsprinzip in zwei Gruppen zu je 10 Personen aufteilen. Er könnte eine Gruppe bitten, eine Lerntechnik einen Monat lang anzuwenden, und die andere Gruppe, „die zweite Lerntechnik für einen Monat zu verwenden“. ein Monat. Monat und lassen Sie alle Schüler die gleiche Prüfung ablegen.

So würden die Daten aussehen:

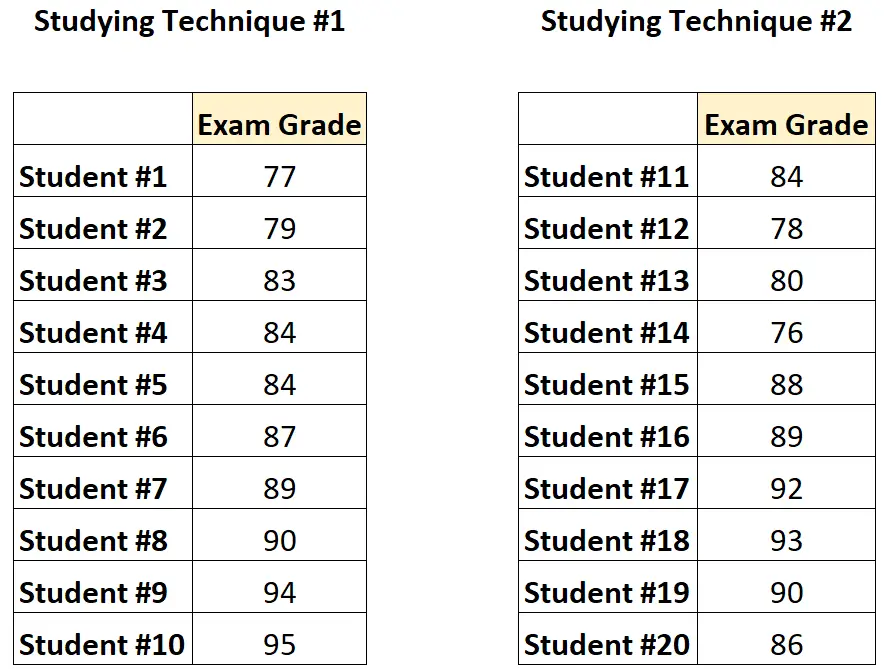
Da die Studierenden einer Gruppe völlig unabhängig von den Studierenden der anderen Gruppe sind, würde der Professor einen ungepaarten T-Test durchführen, um festzustellen, ob die Durchschnittswerte zwischen den beiden Gruppen unterschiedlich sind.

Hypothesen

Sowohl gepaarte als auch ungepaarte t-Tests basieren auf den folgenden Annahmen:

• Die Daten beider Proben wurden mithilfe einer Zufallsstichprobenmethode ermittelt.
• Die Daten beider Stichproben sollten annähernd normalverteilt sein.
• In beiden Stichproben sollte es keine extremen Ausreißer geben.

Diese Annahmen sollten vor der Durchführung eines T-Tests überprüft werden, um die Zuverlässigkeit der Testergebnisse sicherzustellen.

Vorteile und Nachteile

Der gepaarte t-Test bietet folgende Vorteile :

• Es ist eine kleinere Probe erforderlich. Beachten Sie, dass für den gepaarten T-Test im vorherigen Beispiel insgesamt nur 10 Schüler erforderlich waren, während für den ungepaarten T-Test insgesamt 20 Schüler erforderlich waren.
• Jede Stichprobe enthält Individuen mit den gleichen Merkmalen. In beiden Gruppen gibt es garantiert Individuen mit Fähigkeiten, Intellekt usw. gleich, weil in jeder Gruppe die gleichen Individuen vorkommen.

Ein gepaarter T-Test hat jedoch die folgenden potenziellen Nachteile :

• Das Potenzial für eine Reduzierung der Stichprobengröße. Wenn eine Person die Studie verlässt, wird die Stichprobengröße jeder Gruppe um eins reduziert, da diese Person in jeder Gruppe erscheint.
• Das Potenzial für Ordnungseffekte. Reihenfolgeeffekte beziehen sich auf Unterschiede in den Ergebnissen zwischen den beiden Gruppen aufgrund der Reihenfolge, in der die Behandlungen den einzelnen Personen präsentiert wurden. Beispielsweise kann es sein, dass eine Person bei der zweiten Prüfung einfach besser abschneidet, weil sie ihre Prüfungsfähigkeiten verbessert hat, und nicht aufgrund ihrer Lerntechnik.

Berücksichtigen Sie diese Vor- und Nachteile, wenn Sie entscheiden, ob Sie einen gepaarten oder ungepaarten T-Test verwenden möchten.

Zusätzliche Ressourcen

Sehen Sie sich die folgenden Tutorials an, um gepaarte T-Tests besser zu verstehen:

• Eine Einführung in den T-Test für gepaarte Stichproben
• So führen Sie einen T-Test für gepaarte Stichproben in Excel durch

Und nutzen Sie die folgenden Tutorials, um ungepaarte T-Tests (auch T-Tests unabhängiger Stichproben) besser zu verstehen:

• Eine Einführung in den T-Test bei zwei Stichproben
• So führen Sie einen T-Test bei zwei Stichproben in Excel durch