So ermitteln sie den mittelwert und die standardabweichung gruppierter daten

Wir möchten oft den Mittelwert und die Standardabweichung von Daten berechnen, die auf irgendeine Weise gruppiert sind. Angenommen, wir haben die folgenden gruppierten Daten:

Obwohl es nicht möglich ist, den genauen Mittelwert und die Standardabweichung zu berechnen, da wir die Rohdatenwerte nicht kennen, ist es möglich, den Mittelwert und die Standardabweichung zu schätzen.

Die folgenden Schritte erklären, wie das geht.

Verwandte Themen: So finden Sie den gruppierten Datenmodus

Berechnen Sie den Durchschnitt der gruppierten Daten

Wir können die folgende Formel verwenden, um den Mittelwert gruppierter Daten zu schätzen:

Durchschnitt: Σm _i n _i / N

Gold:

• _mi : Die Mitte der i- ^ten Gruppe
• n _i : Die Häufigkeit der i- ^ten Gruppe
• N: Die Gesamtstichprobengröße

So würden wir diese Formel auf unseren vorherigen Datensatz anwenden:

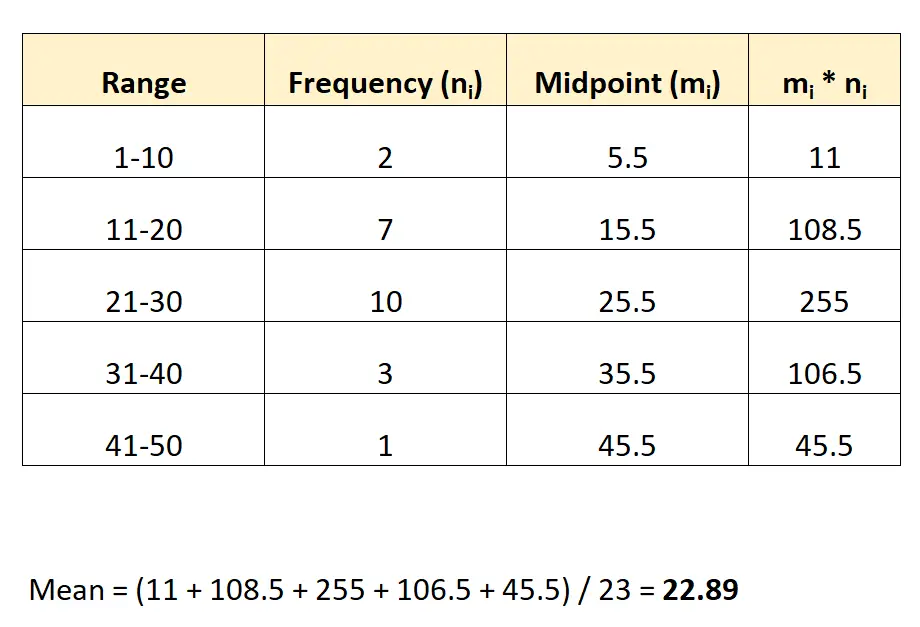
Der Durchschnitt des Datensatzes beträgt 22,89 .

Hinweis: Der Mittelpunkt jeder Gruppe kann durch Bildung des Durchschnitts der unteren und oberen Werte des Bereichs ermittelt werden. Der Mittelpunkt der ersten Gruppe wird beispielsweise wie folgt berechnet: (1+10) / 2 = 5,5.

Berechnen Sie die Standardabweichung gruppierter Daten

Wir können die folgende Formel verwenden, um die Standardabweichung gruppierter Daten zu schätzen:

Standardabweichung: √ Σn _i (m _i -μ) ² / (N-1)

Gold:

• n _i : Die Häufigkeit der i- ^ten Gruppe
• _mi : Die Mitte der i- ^ten Gruppe
• μ : Der Durchschnitt
• N: Die Gesamtstichprobengröße

So würden wir diese Formel auf unseren Datensatz anwenden:

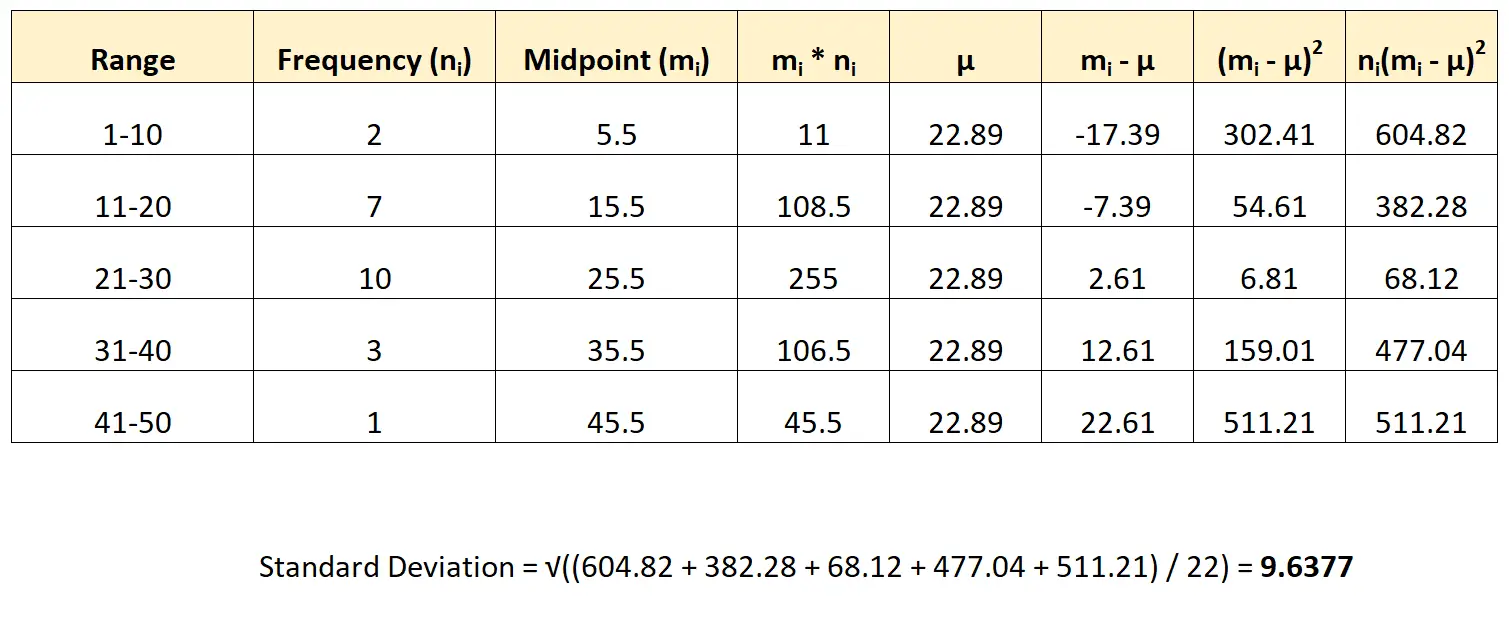Die Standardabweichung des Datensatzes beträgt 9,6377 .

Zusätzliche Ressourcen

So schätzen Sie den Mittelwert und den Median eines beliebigen Histogramms
So berechnen Sie die Perzentilrangfolge für gruppierte Daten
So ermitteln Sie den Median gruppierter Daten