Fishers geringster signifikanter unterschied: definition + beispiel

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Die in einer ANOVA verwendeten Annahmen sind wie folgt:

H ₀ : Die Mittelwerte sind für jede Gruppe gleich.

H _A : Zumindest eine der Möglichkeiten unterscheidet sich von den anderen.

Wenn der p-Wert der ANOVA unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.

Um jedoch genau zu wissen, welche Gruppen sich voneinander unterscheiden, müssen wir einen Post-hoc-Test durchführen.

Ein häufig verwendeter Post-hoc-Test ist der Fisher-Test mit der geringsten signifikanten Differenz .

Um diesen Test durchzuführen, berechnen wir zunächst die folgende Teststatistik:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

Gold:

• t _.025 , _DFw : Der t-kritische Wert der t-Verteilungstabelle mit α = .025 und _DFw entspricht den Freiheitsgraden innerhalb der Gruppen der ANOVA-Tabelle.
• MS _W : Mittlere Quadrate innerhalb der Gruppen in der ANOVA-Tabelle.
• n ₁ , n ₂ : Die Stichprobengrößen jeder Gruppe

Anschließend können wir die mittlere Differenz zwischen den einzelnen Gruppen mit dieser Teststatistik vergleichen. Wenn der Absolutwert der Mittelwertdifferenz zwischen zwei Gruppen größer ist als die Teststatistik, können wir erklären, dass ein statistisch signifikanter Unterschied zwischen den Gruppenmittelwerten besteht.

Das folgende Beispiel zeigt, wie der Fisher-Test auf die geringste signifikante Differenz in der Praxis durchgeführt wird.

Beispiel: Fisher-Least-Significance-Difference-Test

Angenommen, ein Professor möchte wissen, ob drei verschiedene Lerntechniken zu unterschiedlichen Testergebnissen bei den Studenten führen. Um dies zu testen, weist sie nach dem Zufallsprinzip 10 Studenten zu, jede Lerntechnik anzuwenden, und zeichnet ihre Prüfungsergebnisse auf.

Die folgende Tabelle zeigt die Prüfungsergebnisse jedes Studenten basierend auf der verwendeten Lerntechnik:

Der Professor führt eine einfaktorielle ANOVA durch und erhält folgende Ergebnisse:

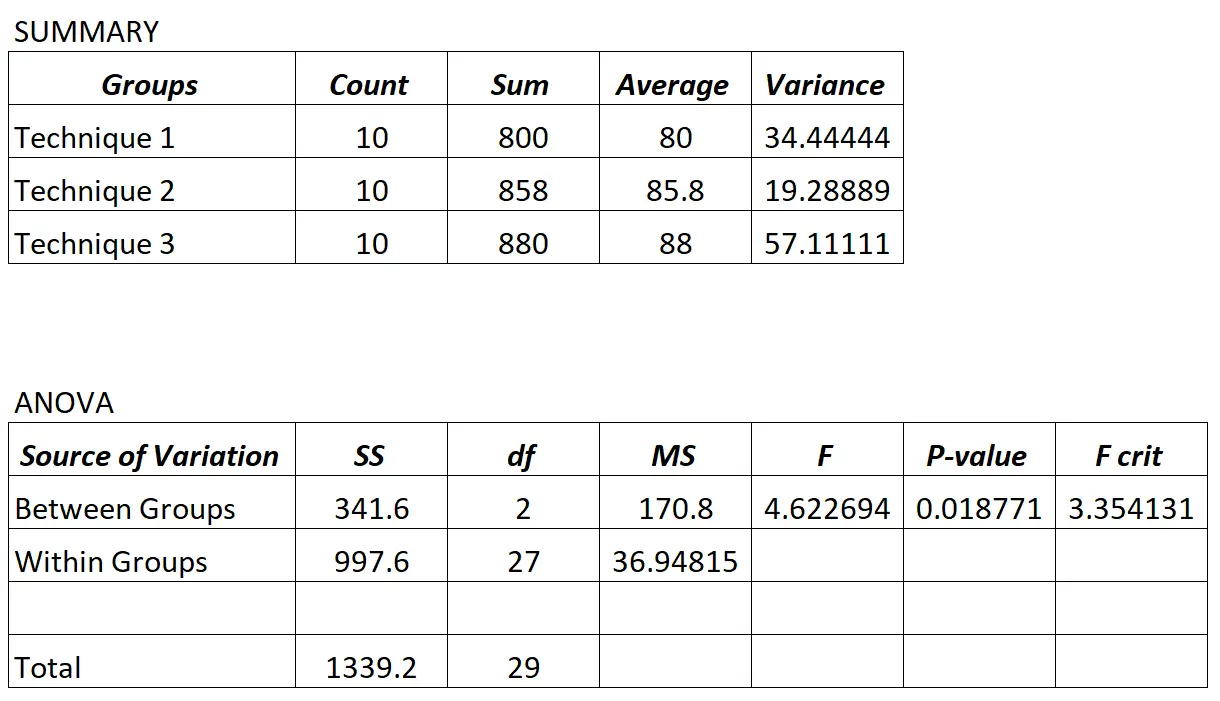
Da der p-Wert in der ANOVA-Tabelle (0,018771) kleiner als 0,05 ist, können wir daraus schließen, dass nicht alle durchschnittlichen Prüfungsergebnisse zwischen den drei Gruppen gleich sind.

Wir können also den Fisher-Test auf die geringste signifikante Differenz durchführen, um zu bestimmen, welche Gruppenmittelwerte unterschiedlich sind.

Mit den Werten aus dem ANOVA-Ergebnis können wir die Fisher-Teststatistik wie folgt berechnen:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• LSD = 2,052 * √ 7,3896
• LSD = 5,578

Anschließend können wir die absolute mittlere Differenz zwischen den einzelnen Gruppen berechnen:

• Technik 1 versus Technik 2: |80 – 85,8| = 5,8
• Technik 1 versus Technik 3: |80 – 88| = 8
• Technik 2 versus Technik 3: |85,8 – 88| = 2,2

Die absoluten Mittelwertunterschiede zwischen Technik 1 und Technik 2 sowie zwischen Technik 1 und Technik 3 sind größer als die Fisher-Teststatistik. Wir können daher den Schluss ziehen, dass diese Techniken zu statistisch signifikant unterschiedlichen durchschnittlichen Prüfungsergebnissen führen.

Wir können auch den Schluss ziehen, dass es keinen signifikanten Unterschied in den durchschnittlichen Prüfungsergebnissen zwischen Technik 2 und Technik 3 gibt.