Geschichtete stichprobe
In diesem Artikel erklären wir, was geschichtete Probenahme ist und wie sie durchgeführt wird. Hier finden Sie die Erklärung der Subtypen der geschichteten Stichprobe und schließlich die Vor- und Nachteile der geschichteten Stichprobe.
Was ist eine geschichtete Stichprobe?
Die geschichtete Stichprobe ist eine statistische Methode, mit der Elemente einer Stichprobe ausgewählt werden, indem die Bevölkerung in Gruppen (sogenannte Schichten) aufgeteilt wird. Das heißt, bei der geschichteten Stichprobe wird die Bevölkerung in Schichten aufgeteilt und Personen aus jeder Schicht werden nach dem Zufallsprinzip ausgewählt, um die gesamte Studienstichprobe zu bilden.
Schichten sind homogene Gruppen, das heißt, Individuen in einer Schicht haben ihre eigenen Merkmale, die sie von anderen Schichten unterscheiden. Ein Individuum kann daher nur einer Schicht angehören.
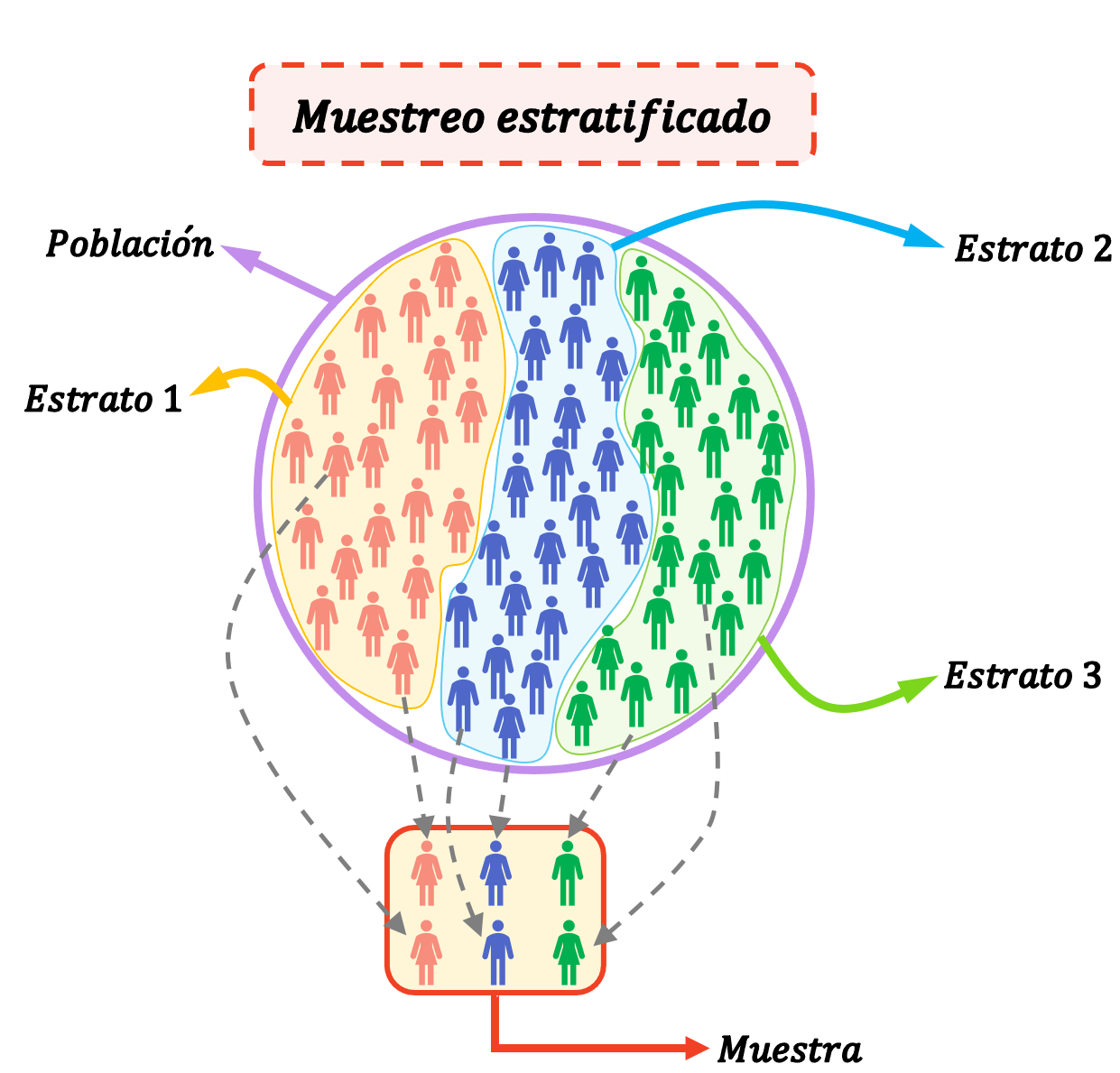
Die geschichtete Stichprobe ist sehr nützlich, wenn die Population aus sehr homogenen Gruppen besteht, die sich stark voneinander unterscheiden.
Logischerweise ergibt die Summe der Größen aller Schichten die Größe der statistischen Grundgesamtheit:
![]()
Ebenso entspricht die Summe der in jeder Schicht gewählten Stichprobengröße der Gesamtstichprobengröße der statistischen Studie:
![]()
Zur Bezeichnung der Grundgesamtheit bzw. Stichprobe unterscheiden wir grundsätzlich zwischen Groß- und Kleinschreibung.
So führen Sie eine geschichtete Stichprobe durch
Die Schritte zur Durchführung einer geschichteten Stichprobe sind wie folgt:
- Definieren Sie die Zielgruppe.
- Wählen Sie die variable Schichtung und wie viele Schichten es geben soll.
- Identifizieren Sie , zu welcher Schicht jedes Element der Bevölkerung gehört.
- Berechnen Sie die Größe jeder Schicht , die Teil der Stichprobe sein wird.
- Wählen Sie nach dem Zufallsprinzip die Elemente aus jeder Schicht aus , die zur Studienstichprobe gehören sollen. Für jede Schicht müssen so viele Elemente ausgewählt werden, wie im vorherigen Schritt festgelegt wurde.
Beachten Sie, dass die Größe, die jede Schicht in der Stichprobe darstellt, nicht nur von der Größe der Schicht abhängt, sondern auch von der Art der geschichteten Stichprobe. Anschließend wird anhand eines Beispiels jede Art der geschichteten Stichprobe erläutert und erläutert, wie die Stichprobengröße jeder Schicht berechnet wird.
Arten der geschichteten Probenahme
Nachdem Sie nun die Definition der geschichteten Stichprobe kennen, sollten Sie wissen, dass es verschiedene Arten der geschichteten Stichprobe gibt, die wie folgt klassifiziert werden:
- Proportional geschichtete Probenahme
- Einheitliche geschichtete Probenahme
- Die Probenahme ist optimal
Jede Art der geschichteten Stichprobe wird im Folgenden ausführlich erläutert, um die Bedeutung der einzelnen Arten besser zu verstehen.
Proportional geschichtete Probenahme
Bei der geschichteten proportionalen Stichprobe oder der proportionalen Allokationsstichprobe ist die Anzahl der Elemente aus jeder Schicht, die Teil der Studienstichprobe sind, proportional zur Größe jeder Schicht.
Wenn also eine Schicht größer ist als eine andere, enthält die endgültige Stichprobe mehr Elemente aus dieser Schicht. Wenn andererseits eine Schicht kleiner ist als eine andere, enthält die Stichprobe der statistischen Analyse weniger Elemente aus dieser Schicht.
Diese Art der geschichteten Stichprobe ist nützlich, wenn die Schichten unterschiedlich groß sind und die Stichprobe mehr Elemente aus den größeren Schichten enthalten soll.
Um die Anzahl der Elemente aus jeder Schicht zu berechnen, die in der Stichprobe enthalten sein werden, muss die Größe jeder Schicht durch die Summe der Größen aller Schichten geteilt werden. Das Ergebnis ist der Anteil der Schicht, der in die Stichprobe einbezogen werden soll. Dieser muss also mit der gewünschten Stichprobengröße multipliziert werden.
![]()
Gold
![]()
ist die gewünschte Gesamtstichprobengröße,
![]()
die Anzahl der Elemente in der Schicht
![]()
in die Stichprobe einbezogen werden,
![]()
Schichtgröße
![]()
, Und
![]()
die Gesamtzahl der Elemente in der Population.
Stellen Sie sich zum Beispiel vor, wir wollten eine Studie in einem Unternehmen mit 150 Mitarbeitern durchführen, eine Stichprobe von 50 Personen nehmen und die Daten nach dem Alter der Mitarbeiter stratifizieren. Wir können die Daten wie folgt klassifizieren:
- Von 20 bis 29 Jahren: 35 Arbeiter
- Von 30 bis 39 Jahren: 57 Mitarbeiter
- Von 40 bis 49 Jahren: 42 Mitarbeiter
- Von 50 bis 59 Jahren: 16 Mitarbeiter
Wenn wir die Daten also proportional schichten, sieht die Stichprobe wie folgt aus:
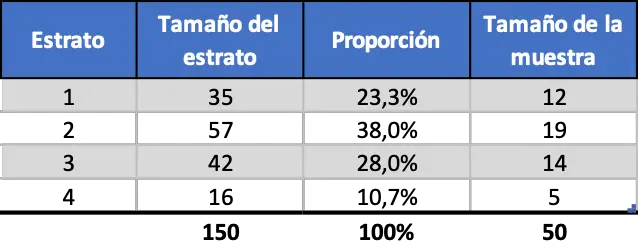
Einheitliche geschichtete Probenahme
Bei der einheitlichen geschichteten Stichprobe oder der einheitlichen Affixationsstichprobe ist die Anzahl der Elemente aus jeder Schicht, die Teil der Untersuchungsstichprobe sind, gleich.
Daher hat bei dieser Art der Stichprobe jede Schicht das gleiche Gewicht. Unabhängig davon, ob eine Schicht mehr oder weniger Individuen hat als eine andere Schicht, werden alle in der Stichprobe durch die gleiche Anzahl von Individuen repräsentiert.
In diesem Fall muss zur Berechnung der Größe der Elemente in jeder Schicht die gewünschte Stichprobengröße durch die Anzahl der vorhandenen Schichten geteilt werden. Mit anderen Worten sollte die folgende Formel verwendet werden:
![]()
Gold
![]()
ist die gewünschte Gesamtstichprobengröße,
![]()
die Anzahl der Elemente in der Schicht
![]()
wer in die Stichprobe einbezogen wird und
![]()
die Anzahl der Schichten, in die die Bevölkerung aufgeteilt wurde.
Da wir gemäß dem vorherigen Beispiel eine Stichprobe von 50 Arbeitnehmern haben wollten und es insgesamt 4 verschiedene Schichten gab, beträgt die Stichprobengröße jeder Schicht:
![]()
Da das Ergebnis eine Dezimalzahl ist, haben einige Schichten 12 Arbeiter und andere 13, bis 50 Arbeiter erreicht sind. Die einheitliche geschichtete Stichprobe lautet also wie folgt:
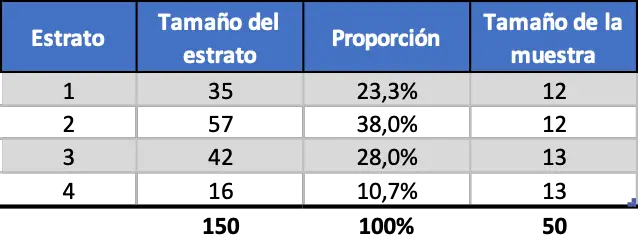
Wie Sie sehen können, ist die Stichprobengröße jeder Schicht unabhängig vom jeweiligen Anteil.
Optimale geschichtete Probenahme
Bei der optimalen geschichteten Stichprobe hängt die Anzahl der Elemente in jeder Schicht proportional von der Variabilität jeder Schicht ab.
Somit haben Schichten mit größerer Variabilität eine größere Stichprobengröße und umgekehrt haben Schichten mit geringerer Variabilität eine kleinere Stichprobengröße.
Die Formel zur Bestimmung, wie viele Elemente aus jeder Schicht Teil der statistischen Studienstichprobe sein werden, lautet wie folgt:
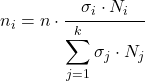
Gold
![]()
ist die gewünschte Gesamtstichprobengröße,
![]()
ist die Anzahl der Elemente in der Schicht
![]()
in die Stichprobe einbezogen werden,
![]()
ist die Standardabweichung (oder typische Abweichung) der Schicht
![]()
, Und
![]()
ist die Größe der Schicht
![]()
.
Vor- und Nachteile der geschichteten Probenahme
Die geschichtete Probenahme hat folgende Vor- und Nachteile:
| Vorteil | Nachteile |
|---|---|
| Es ermöglicht die statistische Untersuchung nicht nur der gesamten Bevölkerung, sondern auch jeder einzelnen Schicht. | Dies ist eine kompliziert zu implementierende Stichprobenmethode. |
| Der bei der geschichteten Stichprobe verursachte Stichprobenfehler ist immer gleich oder kleiner als der einer einfachen Zufallsstichprobe. | Dies ist ein zeitaufwändiger und daher teurer Probenahmeprozess. |
| Es ermöglicht Ihnen, sich das Wissen des Forschers über die Bevölkerung zunutze zu machen. | Um eine Schichtung durchführen zu können, sind viele Informationen über die analysierte Probe erforderlich. |
| Bei der geschichteten Probenahme stellen wir sicher, dass mindestens ein Element aus jeder Schicht in die Probe einbezogen wird. | Um eine Probenahme durchführen zu können, ist es notwendig, den Anteil jeder Schicht zu kennen. |
Das Hauptmerkmal der geschichteten Stichprobe besteht darin, dass sie zur statistischen Analyse jeder Gruppe oder Schicht verwendet wird, in die die Bevölkerung unterteilt wurde. Selbstverständlich kann mit dieser Art der Probenahme auch die gesamte Bevölkerung untersucht werden. Darüber hinaus sind die Vorteile der Datenschichtung größer, wenn sich die Schichten voneinander unterscheiden.
Im Gegenteil bedeutet die Tatsache, dass die Daten geschichtet werden, um die Probenahme durchführen zu können, die Komplexität der Probenahme zu erhöhen, da die geschichtete Probenahme im Vergleich zu anderen Arten der Probenahme komplizierter durchzuführen ist. Diese Eigenschaft impliziert auch, dass es sich um eine teure Stichprobe handelt, da die korrekte Schichtung einige Zeit in Anspruch nimmt.
Ein weiterer Nachteil der geschichteten Stichprobe besteht darin, dass viele Informationen über die zu untersuchende Population erforderlich sind, was bei anderen Stichprobenarten wie der einfachen Zufallsstichprobe nicht erforderlich ist. Dieser Nachteil kann jedoch gemildert werden, wenn der Forscher über umfassende Kenntnisse auf diesem Gebiet verfügt.
Schließlich erhalten wir mit der geschichteten Stichprobe eine Stichprobe, die repräsentativer für die Bevölkerung ist als bei anderen Stichprobenarten, da wir sicherstellen, dass Elemente aus jeder Schicht enthalten sind. Im Gegensatz dazu darf bei anderen Stichproben die resultierende Stichprobe keine Elemente aus irgendeiner Schicht enthalten.