So führen sie eine gewichtete regression der kleinsten quadrate in r durch
Eine der wichtigsten Annahmen der linearen Regression besteht darin, dass die Residuen auf jeder Ebene der Prädiktorvariablen mit gleicher Varianz verteilt sind. Diese Annahme wird als Homoskedastizität bezeichnet.
Wenn diese Annahme nicht berücksichtigt wird, spricht man von Heteroskedastizität in den Residuen. Wenn dies geschieht, werden die Regressionsergebnisse unzuverlässig.
Eine Möglichkeit, dieses Problem zu lösen, ist die Verwendung der gewichteten Regression der kleinsten Quadrate , die den Beobachtungen Gewichte zuweist, sodass Beobachtungen mit geringer Fehlervarianz mehr Gewicht erhalten, da sie im Vergleich zu Beobachtungen mit größerer Fehlervarianz mehr Informationen enthalten.
Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung einer gewichteten Regression der kleinsten Quadrate in R.
Schritt 1: Erstellen Sie die Daten
Der folgende Code erstellt einen Datenrahmen, der die Anzahl der gelernten Stunden und die entsprechende Prüfungspunktzahl für 16 Studenten enthält:
df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))
Schritt 2: Führen Sie eine lineare Regression durch
Als Nächstes verwenden wir die Funktion lm(), um ein einfaches lineares Regressionsmodell anzupassen, das Stunden als Prädiktorvariable und Score als Antwortvariable verwendet:
#fit simple linear regression model model <- lm(score ~ hours, data = df) #view summary of model summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -17,967 -5,970 -0.719 7,531 15,032 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 60,467 5,128 11,791 1.17e-08 *** hours 5,500 1,127 4,879 0.000244 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 9.224 on 14 degrees of freedom Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438
Schritt 3: Testen Sie auf Heteroskedastizität
Als Nächstes erstellen wir ein Diagramm der Residuen und angepassten Werte, um die Heteroskedastizität visuell zu überprüfen:
#create residual vs. fitted plot plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ') #add a horizontal line at 0 abline(0,0)
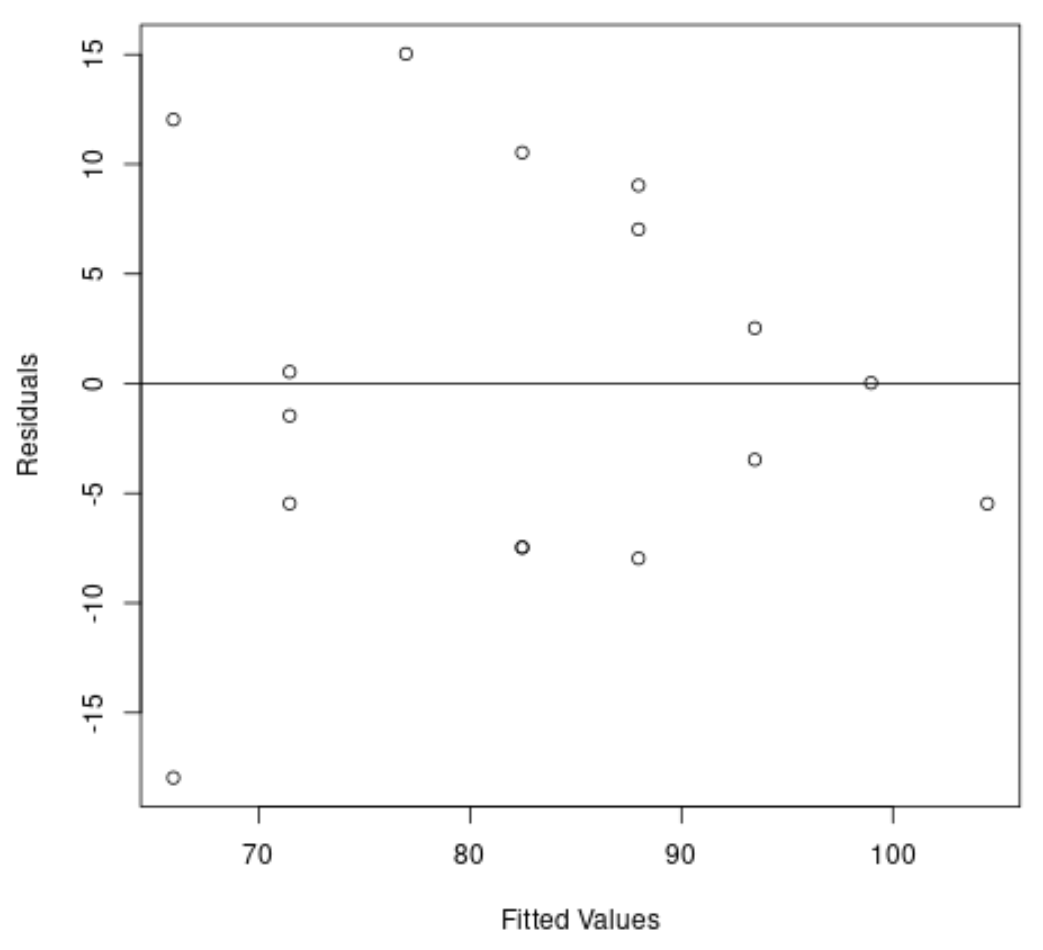
Aus dem Diagramm können wir ersehen, dass die Residuen eine „Kegelform“ haben: Sie sind nicht mit gleicher Varianz über das Diagramm verteilt.
Um die Heteroskedastizität offiziell zu testen, können wir einen Breusch-Pagan-Test durchführen:
#load lmtest package library (lmtest) #perform Breusch-Pagan test bptest(model) studentized Breusch-Pagan test data: model BP = 3.9597, df = 1, p-value = 0.0466
Der Breusch-Pagan-Test verwendet die folgenden Null- und Alternativhypothesen :
- Nullhypothese (H 0 ): Homoskedastizität liegt vor (Residuen sind mit gleicher Varianz verteilt)
- Alternativhypothese ( HA ): Heteroskedastizität liegt vor (Residuen sind nicht mit gleicher Varianz verteilt)
Da der p-Wert des Tests 0,0466 beträgt, lehnen wir die Nullhypothese ab und kommen zu dem Schluss, dass Heteroskedastizität in diesem Modell ein Problem darstellt.
Schritt 4: Führen Sie eine gewichtete Regression der kleinsten Quadrate durch
Da Heteroskedastizität vorliegt, führen wir gewichtete kleinste Quadrate durch, indem wir die Gewichte so festlegen, dass Beobachtungen mit geringerer Varianz mehr Gewicht erhalten:
#define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2
#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)
#view summary of model
summary(wls_model)
Call:
lm(formula = score ~ hours, data = df, weights = wt)
Weighted Residuals:
Min 1Q Median 3Q Max
-2.0167 -0.9263 -0.2589 0.9873 1.6977
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05
Anhand der Ergebnisse können wir erkennen, dass sich die Koeffizientenschätzung für die Stunden -Prädiktorvariable leicht verändert hat und sich die allgemeine Modellanpassung verbessert hat.
Das gewichtete Modell der kleinsten Quadrate weist einen verbleibenden Standardfehler von 1,199 auf, verglichen mit 9,224 im ursprünglichen einfachen linearen Regressionsmodell.
Dies weist darauf hin, dass die vom gewichteten Modell der kleinsten Quadrate erzeugten vorhergesagten Werte viel näher an den tatsächlichen Beobachtungen liegen als die vom einfachen linearen Regressionsmodell erzeugten vorhergesagten Werte.
Das gewichtete Modell der kleinsten Quadrate weist außerdem ein R-Quadrat von 0,6762 auf, verglichen mit 0,6296 im ursprünglichen einfachen linearen Regressionsmodell.
Dies weist darauf hin, dass das gewichtete Modell der kleinsten Quadrate die Varianz der Prüfungsergebnisse besser erklären kann als das einfache lineare Regressionsmodell.
Diese Messungen zeigen, dass das gewichtete Modell der kleinsten Quadrate eine bessere Anpassung an die Daten bietet als das einfache lineare Regressionsmodell.
Zusätzliche Ressourcen
So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine Quantilregression in R durch