Gewichteter durchschnitt

Von Dr. Benjamin Anderson August 6, 2023 Statistiken Keine Kommentare

Hier erklären wir, was der gewichtete Durchschnitt ist und wie er berechnet wird. Sie können eine gelöste Übung zur Ermittlung des gewichteten Durchschnitts sehen. Darüber hinaus können Sie mit dem Rechner am Ende den gewichteten Durchschnitt jedes Datensatzes berechnen.

Was ist der gewichtete Durchschnitt?

Der gewichtete Durchschnitt ist ein Maß für die Zentralität der deskriptiven Statistik. Um den gewichteten Durchschnitt zu berechnen, müssen Sie zunächst alle statistischen Daten mit ihrem Gewicht (oder Gewicht) multiplizieren, dann alle Produkte addieren und schließlich die gewichtete Summe durch die Summe aller Gewichte dividieren.

Mit anderen Worten lautet die Formel für den gewichteten Durchschnitt wie folgt:

Dabei repräsentiert x _i jede Datenprobe und w _i ihr entsprechendes Gewicht.

Je mehr Gewicht also ein Datenelement hat, desto wichtiger wird es für die Berechnung des gewichteten Durchschnitts. Mit anderen Worten: Je höher die Gewichtung eines Datenelements ist, desto stärker beeinflusst es das Ergebnis des gewichteten Durchschnitts.

Der gewichtete Durchschnitt eignet sich insbesondere für die Notenberechnung, da er die Möglichkeit bietet, die während einer Lehrveranstaltung abgelegten Übungen oder Prüfungen mit unterschiedlicher Bedeutung zu bewerten. Der gewichtete Durchschnitt wird auch zur Berechnung des CPI (Consumer Price Index) verwendet, der ein Indikator zur Messung der Preise einer Bevölkerung ist.

Neben dem gewichteten Durchschnitt gibt es auch andere Arten von Durchschnittswerten wie den geometrischen Durchschnitt, den arithmetischen Durchschnitt, den quadratischen Durchschnitt und den harmonischen Durchschnitt.

So berechnen Sie den gewichteten Durchschnitt

Um den gewichteten Durchschnitt zu berechnen, müssen die folgenden Schritte befolgt werden:

Multiplizieren Sie alle statistischen Daten mit ihrem entsprechenden Gewicht.
Addieren Sie alle im vorherigen Schritt berechneten Produkte.
Teilen Sie die gewichtete Summe oben durch die Summe aller Gewichte.
Das erhaltene Ergebnis ist der gewichtete Durchschnitt der statistischen Stichprobe.

👉 Mit dem Rechner unten können Sie den gewichteten Durchschnitt eines beliebigen Datensatzes berechnen.

Beispiel für einen gewichteten Durchschnitt

In Anbetracht der Definition des gewichteten Durchschnitts lösen wir nun eine Übung, um vollständig zu verstehen, wie der gewichtete Durchschnitt aus einem Datensatz ermittelt wird.

Ein Gymnasiast im 1. Jahr erreichte im Fach Mathematik folgende Noten: eine 7 bei der Teilprüfung, die zu 30 % gewertet wird, eine 9 bei der Gruppenarbeit, die zu 20 % gewertet wird, eine 6 bei den im Unterricht gegebenen Übungen mit Gewichtung von 10 % und eine 8 in der Abschlussprüfung, die mit 40 % gewichtet wird. Wie lautet Ihre Abschlussnote für das Fach?

Um die Note des Schülers zu ermitteln, müssen Sie den gewichteten Durchschnitt mit den in der Erklärung angegebenen Werten ermitteln. Dazu wenden wir die gewichtete Durchschnittsformel an:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

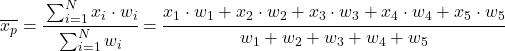
Die Punktzahl jedes Ergebnisses ist der statistische Wert und sein Prozentsatz entspricht der Gewichtung dieses Werts. Daher setzen wir die Werte und Gewichte in die Formel ein und führen die Berechnung des gewichteten Durchschnitts durch:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Die Abschlussnote dieses Schülers in Mathematik beträgt daher 7,7, da es sich hierbei um das Ergebnis aus dem gewichteten Durchschnitt handelt.

Rechner für den gewichteten Durchschnitt

Geben Sie Daten aus einer beliebigen statistischen Stichprobe und deren jeweilige Gewichte in den Rechner unten ein, um den gewichteten Durchschnitt zu berechnen.

Geben Sie die statistischen Daten in das erste Feld und ihre jeweiligen Gewichte in das zweite Feld ein. Sie müssen die Gewichte in derselben Reihenfolge wie die Daten und im Dezimalformat schreiben. Alle Zahlen müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Standardisierte Gewichte

Wie wir gesehen haben, ist die Gewichtung im gewichteten Durchschnitt der Wert, der jedem Datenelement zugewiesen wird, um ihm mehr oder weniger Bedeutung zu verleihen. Wenn Informationen also sehr wichtig sind, haben sie ein sehr hohes Gewicht, wenn Informationen jedoch nicht sehr relevant sind, haben sie ein sehr niedriges Gewicht.

Nun, die normalisierte Gewichtung ist eine Art der Gewichtung, die verwendet wird, um den gewichteten Durchschnitt zu ermitteln, ohne dass eine Division durchgeführt werden muss.

Das normalisierte Gewicht ist das Gewicht eines Datenelements geteilt durch die Summe aller Gewichte.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

Die Summe aller normalisierten Gewichte ist daher gleich eins:

$\sum_{i=1}^N w_i'=1$

Um also den gewichteten Durchschnitt mit den normalisierten Gewichten zu berechnen , multiplizieren Sie einfach jedes Datenelement mit seinem normalisierten Gewicht:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

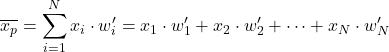
Zum Beispiel haben wir eine statistische Stichprobe, deren Daten 24, 35, 17, 41 sind und deren jeweilige Gewichte 4, 9, 6, 3 sind. Um den gewichteten Durchschnitt dieses Datensatzes zu ermitteln, können wir zunächst die normalisierten Gewichte durch Division berechnen jedes Gewicht durch die Summe aller Gewichte:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

Und jetzt multiplizieren Sie einfach alle Daten mit ihrem normalisierten Gewicht und das Ergebnis ist der gewichtete Durchschnitt:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Differenz zwischen gewichtetem Durchschnitt und arithmetischem Durchschnitt

Die Berechnung des gewichteten Durchschnitts und des arithmetischen Durchschnitts erfolgt auf die gleiche Weise, da ähnliche Operationen durchgeführt werden müssen. Bei der gewichteten Mittelung wird jeder Datenpunkt mit seinem Gewicht multipliziert und durch die Summe der Gewichte dividiert. Bei der arithmetischen Mittelung werden jedoch alle Daten addiert und durch die Gesamtzahl der Datenpunkte dividiert.

Der Unterschied zwischen dem gewichteten Durchschnitt und dem arithmetischen Durchschnitt liegt in seinem Konzept, da beim arithmetischen Durchschnitt davon ausgegangen wird, dass alle Daten den gleichen Wert haben, beim gewichteten Durchschnitt jedoch jede Daten ein anderes Gewicht hat.

Beachten Sie, dass der gewichtete Durchschnitt dem arithmetischen Durchschnitt entspricht, wenn alle Gewichte gleich sind. Den mathematischen Beweis können Sie unten sehen:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen