Eine einführung in die gleichverteilung

Die Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, bei der jeder Wert zwischen einem Intervall von a bis b die gleiche Eintrittswahrscheinlichkeit hat.

Wenn eine Zufallsvariable X einer Gleichverteilung folgt, kann die Wahrscheinlichkeit, dass X einen Wert zwischen x ₁ und x ₂ annimmt, mit der folgenden Formel ermittelt werden:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

Gold:

• x ₁ : der niedrigere Zinswert
• x ₂ : der obere interessierende Wert
• a: der minimal mögliche Wert
• b: der maximal mögliche Wert

Nehmen wir zum Beispiel an, dass das Gewicht der Delfine gleichmäßig zwischen 100 und 150 Pfund verteilt ist.

Wenn wir einen Delfin zufällig auswählen, können wir die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, dass der ausgewählte Delfin zwischen 120 und 130 Pfund wiegt:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0,2

Die Wahrscheinlichkeit, dass der ausgewählte Delfin zwischen 120 und 130 Pfund wiegt, beträgt 0,2 .

Visualisieren Sie eine gleichmäßige Verteilung

Wenn wir ein Dichtediagramm erstellen, um die gleichmäßige Verteilung zu visualisieren, würde es wie folgt aussehen:

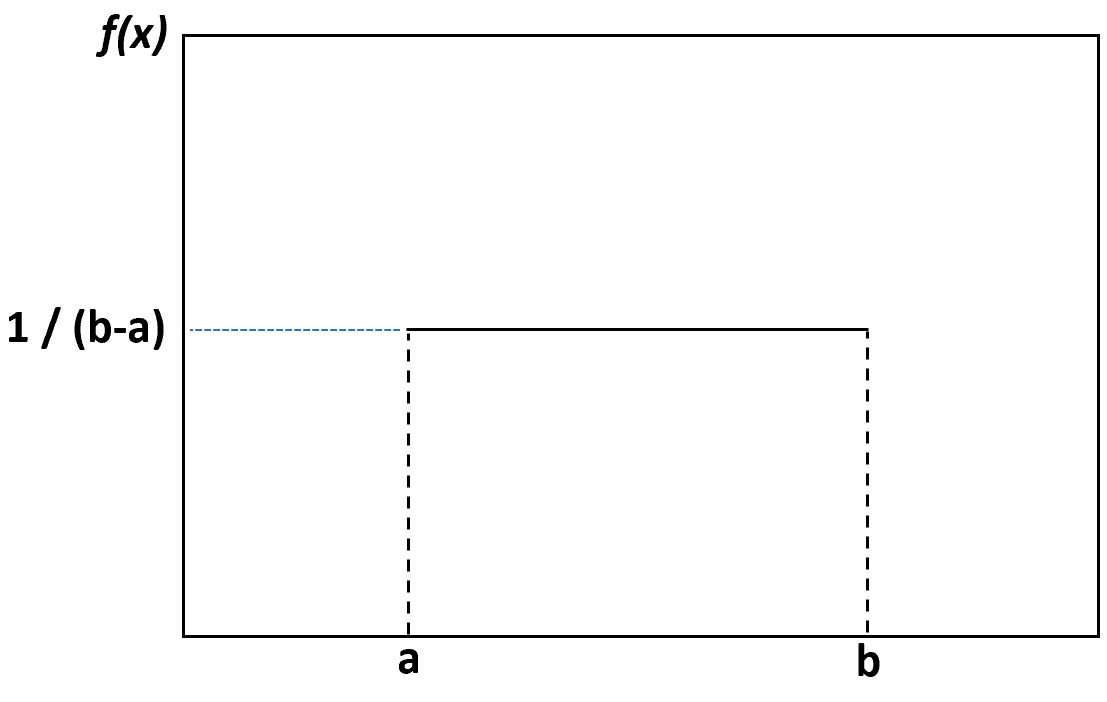
Jeder Wert zwischen der Untergrenze a und der Obergrenze b hat die gleiche Eintrittswahrscheinlichkeit und jeder Wert außerhalb dieser Grenzen hat eine Wahrscheinlichkeit von Null.

In unserem vorherigen Beispiel haben wir beispielsweise gesagt, dass das Gewicht von Delfinen gleichmäßig zwischen 100 und 150 Pfund verteilt ist. So visualisieren Sie diese Verteilung:

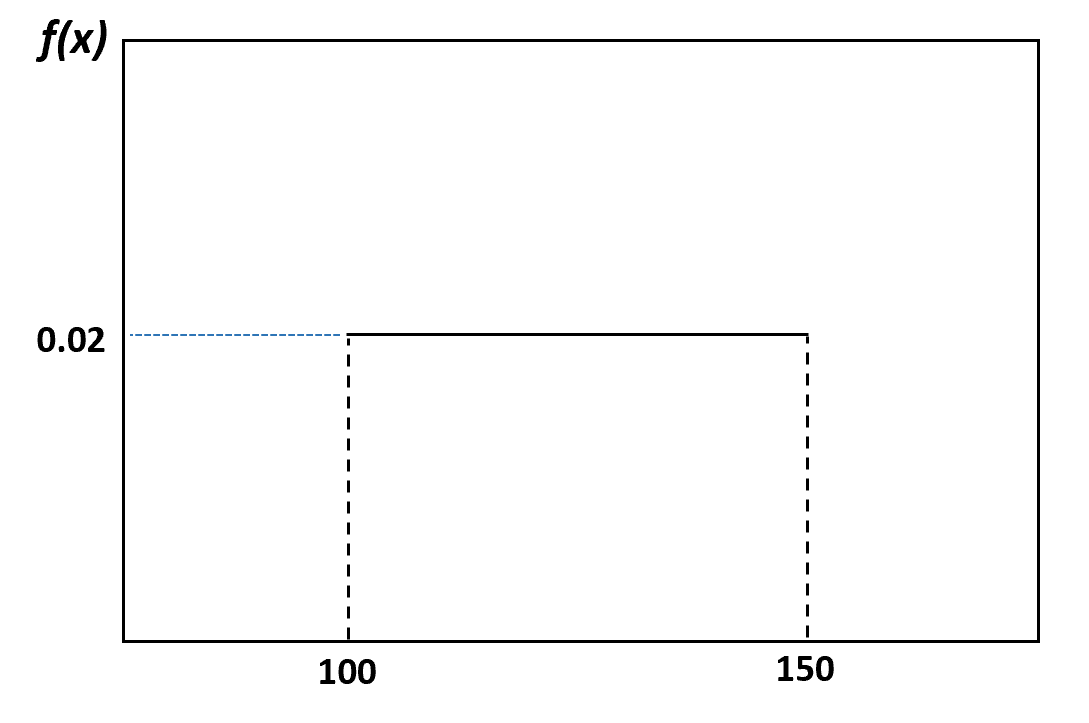
Und die Wahrscheinlichkeit, dass ein zufällig ausgewählter Delfin zwischen 120 und 130 Pfund wiegt, lässt sich wie folgt visualisieren:

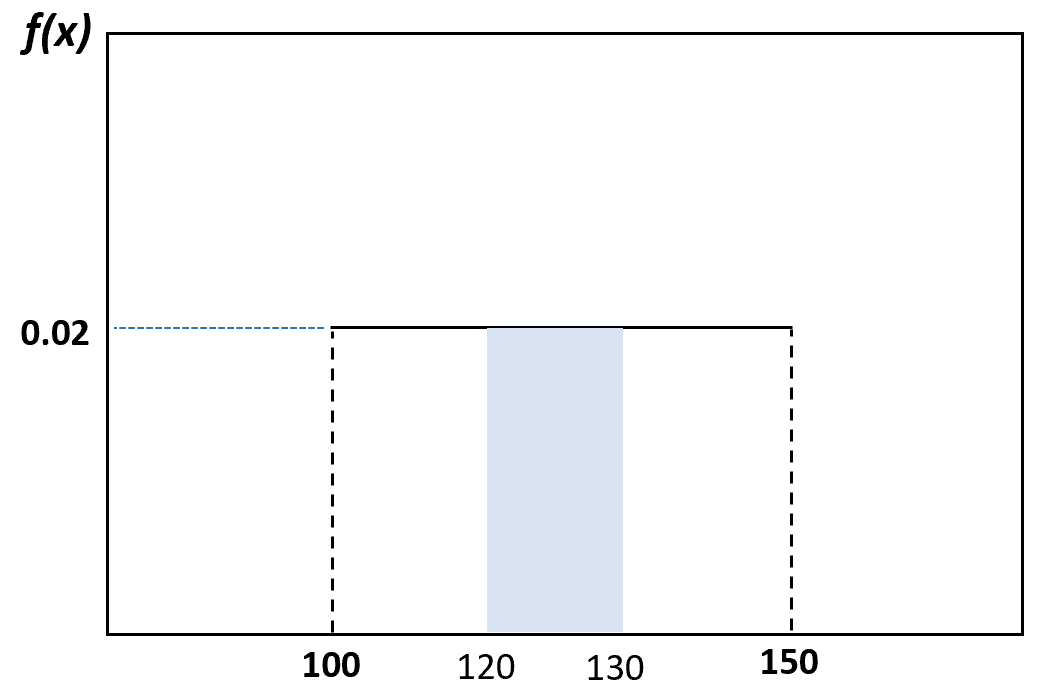
Eigenschaften der Gleichverteilung

Die Gleichverteilung hat folgende Eigenschaften:

• Durchschnitt: (a + b) / 2
• Median: (a + b) / 2
• Standardabweichung: √ (b – a) ² / 12
• Differenz: (b – a) ² / 12

Nehmen wir zum Beispiel an, dass das Gewicht der Delfine gleichmäßig zwischen 100 und 150 Pfund verteilt ist.

Für diese Verteilung könnten wir folgende Eigenschaften berechnen:

• Durchschnittsgewicht: (a + b) / 2 = (150 + 100) / 2 = 125
• Mediangewicht: (a + b) / 2 = (150 + 100) / 2 = 125
• Standardabweichung des Gewichts: √ (150 – 100) ² / 12 = 14,43
• Gewichtsvariation: (150 – 100) ² / 12 = 208,33

Probleme mit einheitlichen Vertriebspraktiken

Verwenden Sie die folgenden Übungsaufgaben, um Ihr Wissen über die Gleichverteilung zu testen.

Frage 1: Alle 20 Minuten kommt ein Bus an eine Haltestelle. Wenn Sie an der Bushaltestelle ankommen, wie hoch ist die Wahrscheinlichkeit, dass der Bus in 8 Minuten oder weniger ankommt?

Lösung 1: Die minimale Wartezeit beträgt 0 Minuten und die maximale Wartezeit beträgt 20 Minuten. Der untere Zinswert beträgt 0 Minuten und der obere Zinswert beträgt 8 Minuten.

Wir würden die Wahrscheinlichkeit also wie folgt berechnen:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Frage 2: Die Dauer eines NBA-Spiels verteilt sich gleichmäßig zwischen 120 und 170 Minuten. Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewähltes NBA-Spiel länger als 155 Minuten dauert?

Lösung 2: Die Mindestdauer beträgt 120 Minuten und die Höchstdauer 170 Minuten. Der untere Zinswert beträgt 155 Minuten und der obere Zinswert beträgt 170 Minuten.

Wir würden die Wahrscheinlichkeit also wie folgt berechnen:

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Frage 3: Das Gewicht einer bestimmten Froschart liegt gleichmäßig zwischen 15 und 25 Gramm. Wenn Sie zufällig einen Frosch auswählen, wie hoch ist die Wahrscheinlichkeit, dass er zwischen 17 und 19 Gramm wiegt?

Lösung 3: Das Mindestgewicht beträgt 15 Gramm und das Höchstgewicht 25 Gramm. Der untere Zinswert beträgt 17 Gramm und der obere Zinswert beträgt 19 Gramm.

Wir würden die Wahrscheinlichkeit also wie folgt berechnen:

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Hinweis: Wir können den Uniform Distribution Calculator verwenden, um unsere Antworten auf jedes dieser Probleme zu überprüfen.