So erstellen sie eine korrelationsmatrix in google sheets
Eine Möglichkeit, die Beziehung zwischen zwei Variablen zu quantifizieren, ist die Verwendung des Pearson-Korrelationskoeffizienten , der ein Maß für den linearen Zusammenhang zwischen zwei Variablen ist . Es hat einen Wert zwischen -1 und 1, wobei:
- -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
- 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
- 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an
Je weiter der Korrelationskoeffizient von Null entfernt ist, desto stärker ist die Beziehung zwischen den beiden Variablen.
In manchen Fällen möchten wir jedoch die Korrelation zwischen mehreren Variablenpaaren verstehen. In diesen Fällen können wir eine Korrelationsmatrix erstellen, bei der es sich um eine quadratische Tabelle handelt, die die Korrelationskoeffizienten zwischen mehreren paarweisen Kombinationen von Variablen zeigt.
In diesem Tutorial wird erläutert, wie Sie eine Korrelationsmatrix in Google Sheets erstellen und interpretieren.
So erstellen Sie eine Korrelationsmatrix in Google Sheets
Nehmen wir an, wir haben den folgenden Datensatz, der die durchschnittliche Anzahl an Punkten, Rebounds und Assists für 10 Basketballspieler zeigt:
Um eine Korrelationsmatrix für diesen Datensatz zu erstellen, können wir die Funktion CORREL() mit der folgenden Syntax verwenden:
COVAR(data_y, data_x)
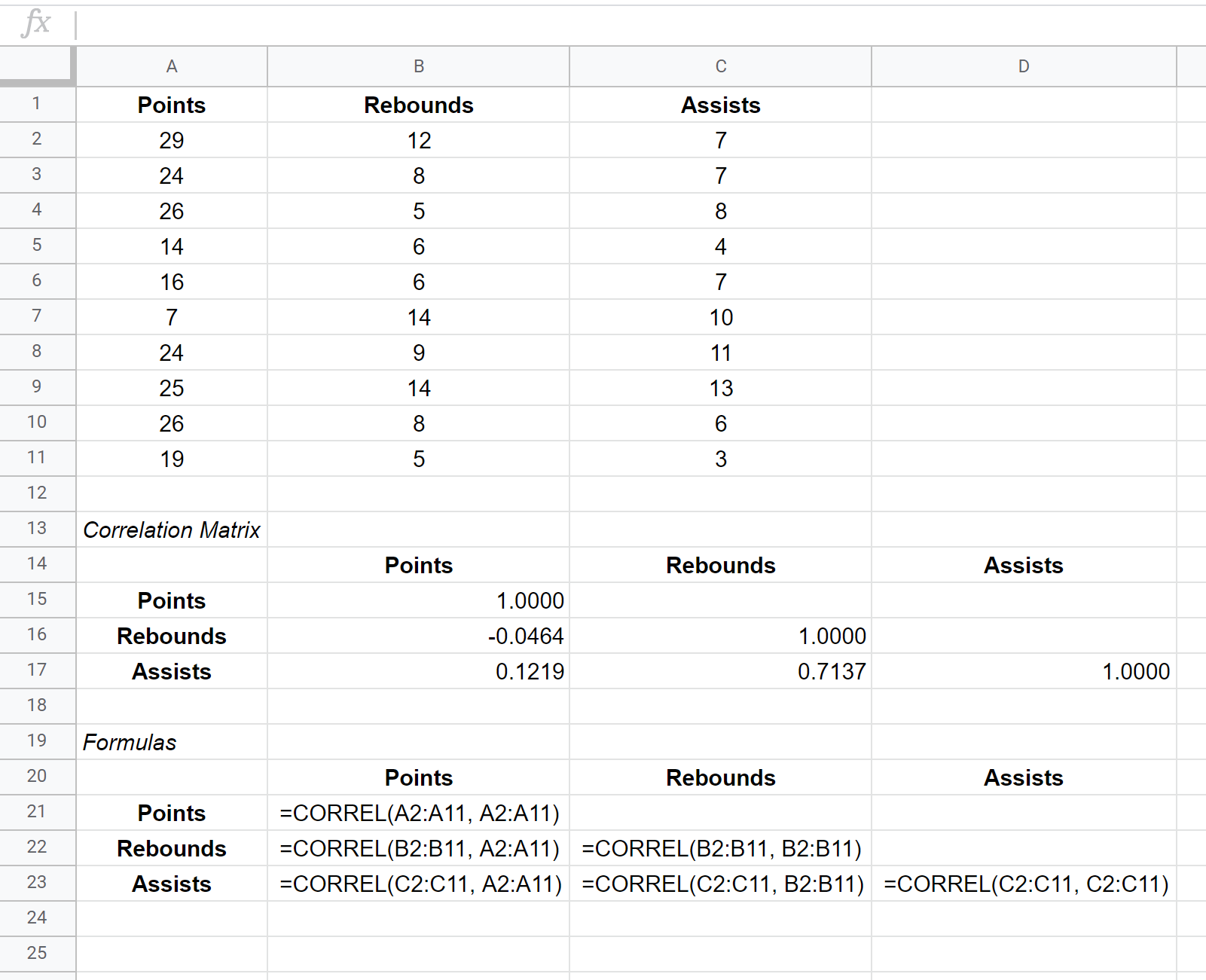
Die Kovarianzmatrix für diesen Datensatz wird in den Zellen B15:D17 angezeigt, während die zur Erstellung der Kovarianzmatrix verwendeten Formeln in den Zellen B21:D23 unten angezeigt werden:
So interpretieren Sie eine Korrelationsmatrix
Die Werte in den einzelnen Zellen der Korrelationsmatrix geben Auskunft über den Pearson-Korrelationskoeffizienten zwischen jeder paarweisen Kombination von Variablen. Zum Beispiel:
Korrelation zwischen Punkten und Rebounds: -0,0464. Punkte und Rebounds korrelieren leicht negativ, aber dieser Wert liegt so nahe bei Null, dass es keine eindeutigen Hinweise auf einen signifikanten Zusammenhang zwischen diesen beiden Variablen gibt.
Korrelation zwischen Punkten und Assists: 0,1219. Punkte und Assists korrelieren leicht positiv, aber auch dieser Wert liegt recht nahe bei Null, sodass es keine eindeutigen Hinweise auf einen signifikanten Zusammenhang zwischen diesen beiden Variablen gibt.
Korrelation zwischen Rebounds und Assists: 0,7137. Rebounds und Assists korrelieren stark positiv. Das heißt, dass Spieler, die mehr Rebounds haben, tendenziell auch mehr Assists haben.
Beachten Sie, dass die Diagonalwerte der Korrelationsmatrix alle 1 sind, da die Korrelation zwischen einer Variablen und sich selbst immer 1 ist. In der Praxis ist diese Zahl nicht sinnvoll zu interpretieren.
Zusätzliche Ressourcen
So lesen Sie eine Korrelationsmatrix
So erstellen Sie eine Korrelationsmatrix in Excel