So bestimmen sie, ob eine wahrscheinlichkeitsverteilung gültig ist

Eine Wahrscheinlichkeitsverteilung gibt uns die Wahrscheinlichkeit an, mit der eine Zufallsvariable bestimmte Werte annimmt.

Damit eine Wahrscheinlichkeitsverteilung gültig ist, muss sie zwei Anforderungen erfüllen:

1. Jede Wahrscheinlichkeit muss zwischen 0 und 1 liegen.

2. Die Summe der Wahrscheinlichkeiten muss 1 ergeben.

Wenn diese beiden Bedingungen erfüllt sind, ist die Wahrscheinlichkeitsverteilung gültig.

Die folgenden Beispiele zeigen, wie man prüft, ob unterschiedliche Wahrscheinlichkeitsverteilungen gültig sind.

Beispiel 1: In einem Fußballspiel erzielte Tore

Die folgende Wahrscheinlichkeitsverteilung zeigt die Wahrscheinlichkeit, dass eine bestimmte Fußballmannschaft in einem Spiel eine bestimmte Anzahl Tore schießt:

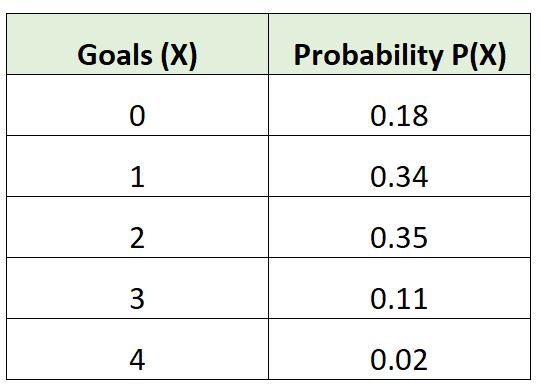
Überprüfen wir, ob diese Wahrscheinlichkeitsverteilung beide Anforderungen erfüllt, um gültig zu sein:

1. Jede Wahrscheinlichkeit muss zwischen 0 und 1 liegen.

Wir können sehen, dass jede einzelne Wahrscheinlichkeit zwischen 0 und 1 liegt.

2. Die Summe der Wahrscheinlichkeiten muss 1 ergeben.

Wir können sehen, dass die Summe der Wahrscheinlichkeiten 1 ergibt:

Summe = 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1

Beide Bedingungen sind erfüllt, daher ist diese Wahrscheinlichkeitsverteilung gültig .

Beispiel 2: Verkäufe in einem Monat

Die folgende Wahrscheinlichkeitsverteilung zeigt die Wahrscheinlichkeit, dass ein bestimmter Verkäufer im kommenden Monat eine bestimmte Anzahl von Verkäufen tätigen wird:

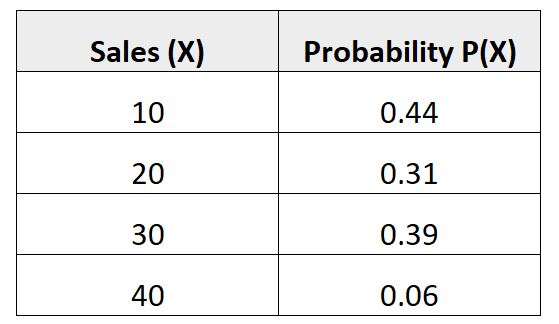
Überprüfen wir, ob diese Wahrscheinlichkeitsverteilung beide Anforderungen erfüllt, um gültig zu sein:

1. Jede Wahrscheinlichkeit muss zwischen 0 und 1 liegen.

Wir können sehen, dass jede einzelne Wahrscheinlichkeit zwischen 0 und 1 liegt.

2. Die Summe der Wahrscheinlichkeiten muss 1 ergeben.

Wir sehen, dass die Summe der Wahrscheinlichkeiten nicht 1 ergibt:

Summe = 0,44 + 0,31 + 0,39 + 0,06 = 1,2

Beide Bedingungen sind nicht erfüllt und diese Wahrscheinlichkeitsverteilung ist daher ungültig .

Beispiel 3: Anzahl der Batterieausfälle

Die folgende Wahrscheinlichkeitsverteilung gibt Auskunft über die Wahrscheinlichkeit, dass bei einem bestimmten Fahrzeug über einen Zeitraum von 10 Jahren eine bestimmte Anzahl von Batterieausfällen auftritt:

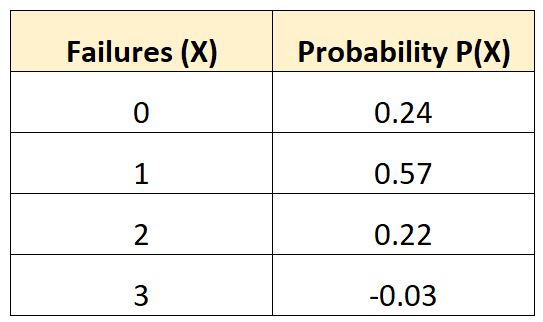
Überprüfen wir, ob diese Wahrscheinlichkeitsverteilung beide Anforderungen erfüllt, um gültig zu sein:

1. Jede Wahrscheinlichkeit muss zwischen 0 und 1 liegen.

Wir können sehen, dass jede einzelne Wahrscheinlichkeit nicht zwischen 0 und 1 liegt.

Die letzte Wahrscheinlichkeit in der Tabelle ist ein negativer Wert.

2. Die Summe der Wahrscheinlichkeiten muss 1 ergeben.

Wir können sehen, dass die Summe der Wahrscheinlichkeiten 1 ergibt:

Summe = 0,24 + 0,57 + 0,22 – 0,03 = 1

Beide Bedingungen sind nicht erfüllt und diese Wahrscheinlichkeitsverteilung ist daher ungültig .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Wahrscheinlichkeitsverteilungen:

So ermitteln Sie den Mittelwert einer Wahrscheinlichkeitsverteilung
So ermitteln Sie die Varianz einer Wahrscheinlichkeitsverteilung
So ermitteln Sie die Standardabweichung einer Wahrscheinlichkeitsverteilung