Was gilt als gutes oder schlechtes residualplot?
In der Regressionsanalyse ist ein Residuendiagramm eine Art Diagramm, das die angepassten Werte eines Regressionsmodells auf der x-Achse und die Residuen des Modells entlang der y-Achse anzeigt.
Bei der visuellen Prüfung eines Restlayouts achten wir im Allgemeinen auf zwei Dinge, um festzustellen, ob das Layout „gut“ oder „schlecht“ ist:
1. Zeigen die Residuen einen klaren Trend?
- In einem „guten“ Residuendiagramm zeigen die Residuen keinen klaren Trend.
- In einem „schlechten“ Residuendiagramm weisen die Residuen ein bestimmtes Muster auf, beispielsweise eine Kurve oder Welle. Dies weist darauf hin, dass das von uns verwendete Regressionsmodell keine angemessene Anpassung an die Daten liefert.
2. Nimmt die Varianz der Residuen systematisch zu oder ab?
- In einem „guten“ Residuendiagramm sind die Residuen zufällig um Null herum verstreut, ohne dass es zu einer systematischen Zunahme oder Abnahme der Varianz kommt.
- In einem „schlechten“ Residuendiagramm nimmt die Varianz der Residuen systematisch zu oder ab.
Wenn ein Residuendiagramm mit „gut“ bewertet wird, bedeutet dies, dass wir den Ergebnissen des Regressionsmodells vertrauen können und dass die Modellkoeffizienten sicher interpretiert werden können.
Wenn ein Residuendiagramm jedoch als „schlecht“ bewertet wird, bedeutet dies, dass die Modellergebnisse unzuverlässig sind und wir ein anderes Regressionsmodell an die Daten anpassen müssen.
Die folgenden Beispiele erläutern, wie „gute“ und „schlechte“ Residuendiagramme in der Praxis interpretiert werden.
Beispiel 1: eine „gute“ Restspur
Angenommen, wir passen ein Regressionsmodell an und erhalten das folgende Residuendiagramm:
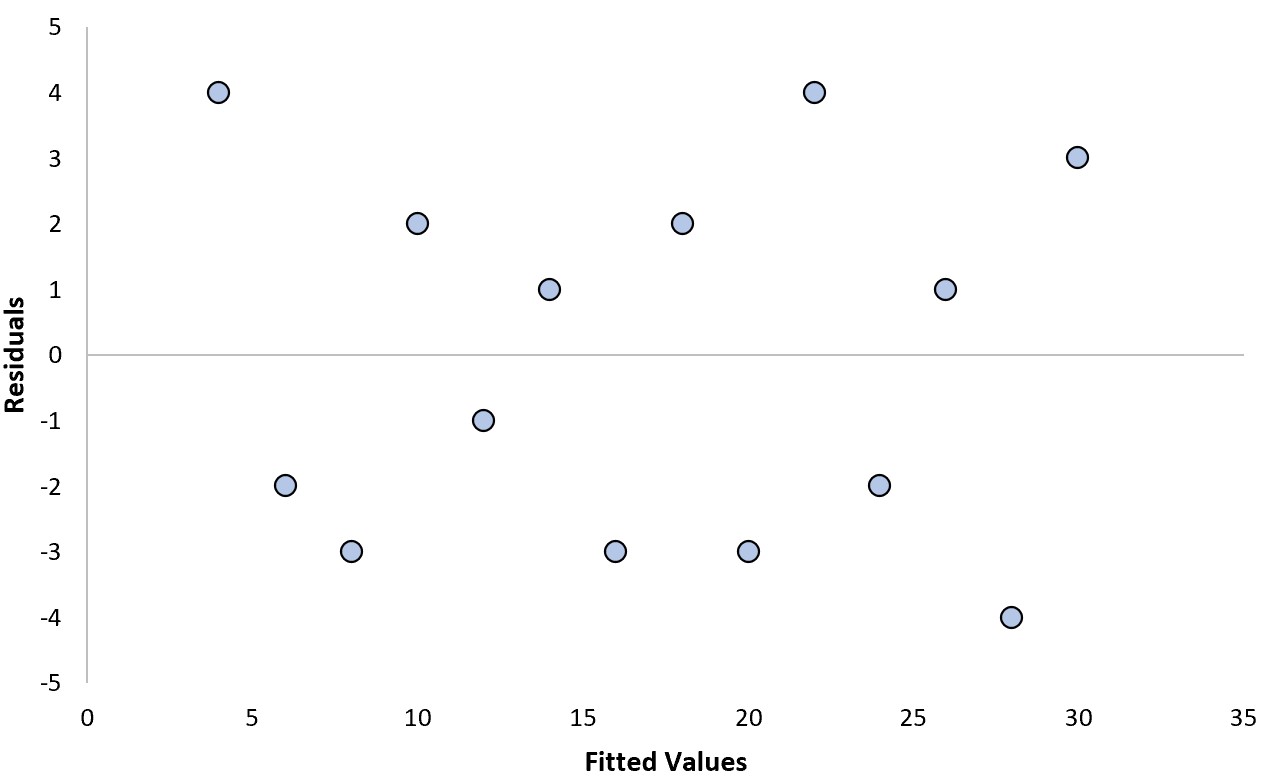
Wir können die folgenden zwei Fragen beantworten, um festzustellen, ob es sich um ein „gutes“ Residuendiagramm handelt:
1. Zeigen die Residuen einen klaren Trend?
Nein. Die Residuen sind zufällig um den Nullpunkt verteilt und weisen kein klares Muster auf.
2. Nimmt die Varianz der Residuen systematisch zu oder ab?
Nein. Die Residuen haben auf jeder Ebene der angepassten Werte eine ziemlich konstante Varianz (dh den Abstand zwischen den Residuen und dem Nullwert).
Da wir beide Fragen mit „Nein“ beantwortet haben, würden wir dies als „gutes“ Restdiagramm betrachten.
Daher können wir den Ergebnissen des Regressionsmodells vertrauen und die Modellkoeffizienten sicher interpretieren.
Beispiel 2: ein „schlechtes“ Residuendiagramm mit einem klaren Modell
Angenommen, wir passen ein Regressionsmodell an und erhalten das folgende Residuendiagramm:
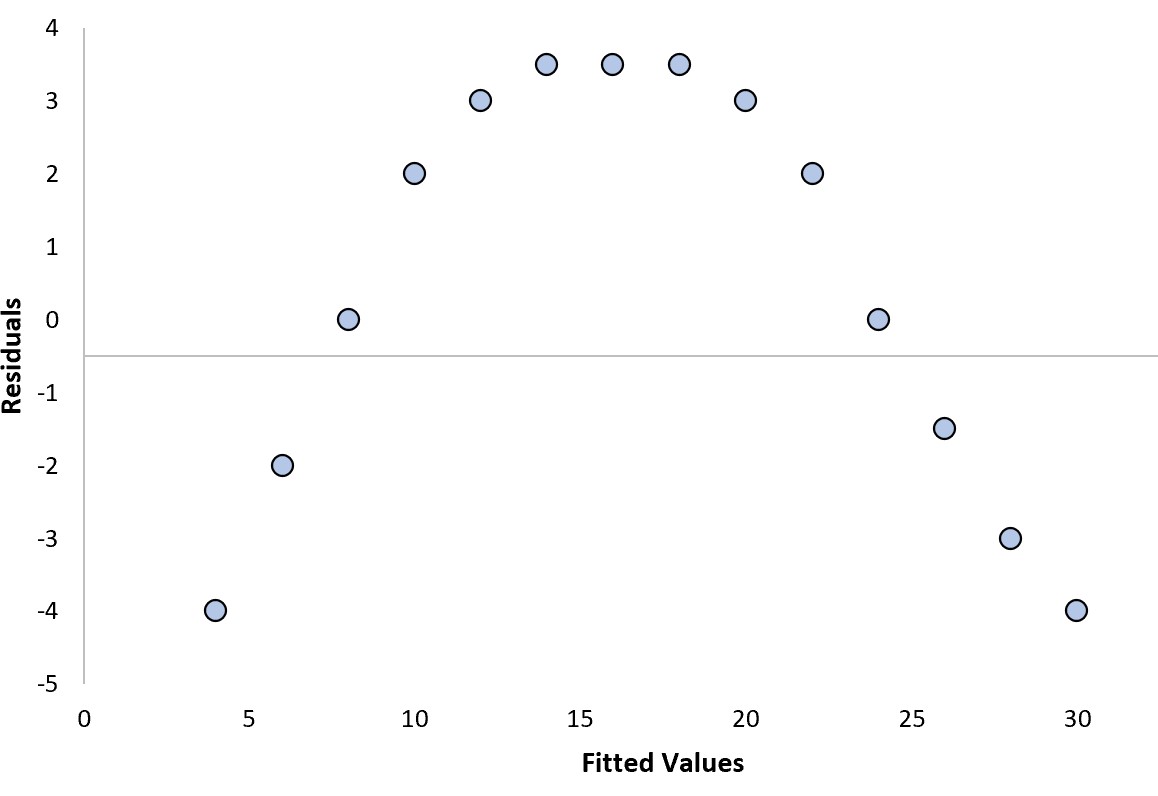
Wir können die folgenden zwei Fragen beantworten, um festzustellen, ob es sich um ein „gutes“ Residuendiagramm handelt:
1. Zeigen die Residuen einen klaren Trend?
Ja . Die Rückstände zeigen ein geschwungenes Muster.
2. Nimmt die Varianz der Residuen systematisch zu oder ab?
Ja . Die Residuen weisen auf verschiedenen Ebenen der angepassten Werte unterschiedliche Varianzniveaus auf.
Da wir mindestens eine dieser Fragen mit „Ja“ beantwortet haben, würden wir dies als „schlechte“ Restdarstellung betrachten.
Das bedeutet, dass das Regressionsmodell keine gute Anpassung an die Daten liefert.
Insbesondere das gekrümmte Muster im Residuendiagramm weist darauf hin, dass ein lineares Regressionsmodell die Daten nicht anpasst und dass ein quadratisches Regressionsmodell wahrscheinlich bessere Ergebnisse liefern würde.
Beispiel 3: ein „schlechtes“ Residuendiagramm mit zunehmender Varianz
Angenommen, wir passen ein Regressionsmodell an und erhalten das folgende Residuendiagramm:
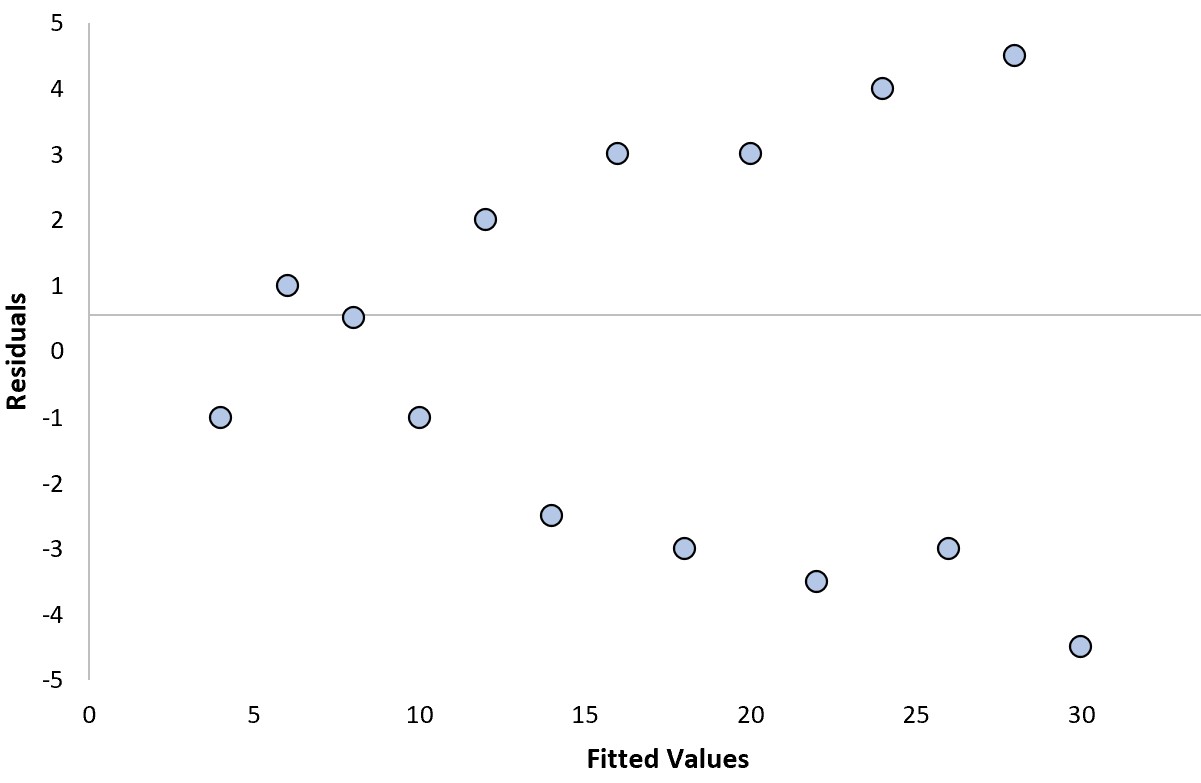
Wir können die folgenden zwei Fragen beantworten, um festzustellen, ob es sich um ein „gutes“ Residuendiagramm handelt:
1. Zeigen die Residuen einen klaren Trend?
Nein. Es gibt keinen klaren Trend bei den Residuen.
2. Nimmt die Varianz der Residuen systematisch zu oder ab?
Ja . Die Varianz der Residuen nimmt mit zunehmenden angepassten Werten zu.
Da wir mindestens eine dieser Fragen mit „Ja“ beantwortet haben, würden wir dies als „schlechte“ Restdarstellung betrachten.
In diesem speziellen Beispiel leiden die Residuen unter Heteroskedastizität , was sich auf eine ungleiche Varianz der Residuen auf verschiedenen Ebenen der angepassten Werte bezieht.
Dies bedeutet, dass die Ergebnisse des Regressionsmodells möglicherweise nicht zuverlässig sind.
In diesem Artikel erfahren Sie, wie Sie das Problem der Heteroskedastizität in einem Regressionsmodell auf verschiedene Arten lösen können.
Zusätzliche Ressourcen
In den folgenden Tutorials wird erläutert, wie Sie mit unterschiedlicher Statistiksoftware Residuendiagramme erstellen:
So erstellen Sie ein Residuendiagramm in R
So erstellen Sie ein Restdiagramm in Python
So erstellen Sie ein Residuendiagramm in Excel
So erstellen Sie ein Restdiagramm in SAS