So führen sie einen chi-quadrat-test von hand durch (schritt für schritt)

Mithilfe eines Chi-Quadrat-Anpassungstests wird ermittelt, ob eine kategoriale Variable einer hypothetischen Verteilung folgt oder nicht.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie manuell einen Chi-Quadrat-Anpassungstest durchführen.

Chi-Quadrat-Anpassungstest von Hand

Angenommen, wir glauben, dass ein bestimmter Würfel richtig ist. Mit anderen Worten: Wir glauben, dass die Würfel bei einem gegebenen Wurf mit derselben Wahrscheinlichkeit auf einer 1, einer 2, einer 3, einer 4, einer 5 oder einer 6 landen.

Um dies zu testen, werfen wir es 60 Mal und notieren jedes Mal die Zahl, auf der es landet. Die Ergebnisse sind wie folgt:

• 1 :8 mal
• 2 : 12 mal
• 3 : 18 Mal
• 4 :9 mal
• 5 :7 mal
• 6 : 6 Mal

Befolgen Sie die folgenden Schritte, um einen Chi-Quadrat-Anpassungstest durchzuführen und festzustellen, ob die Würfel fair sind.

Schritt 1: Definieren Sie die Null- und Alternativhypothese

• H ₀ (Null): Die Würfel haben die gleiche Wahrscheinlichkeit, auf jeder Zahl zu landen.
• H ₁ (Alternative): Die Würfel haben nicht die gleiche Wahrscheinlichkeit, auf jeder Zahl zu landen.

Schritt 2: Berechnen Sie die beobachteten und erwarteten Häufigkeiten

Als nächstes erstellen wir eine Tabelle der beobachteten und erwarteten Häufigkeiten für jede Zahl auf den Würfeln:

Hinweis : Wenn wir glauben, dass der Würfel fair ist, bedeutet das, dass wir erwarten, dass er auf jeder Zahl gleich oft landet – in diesem Fall jeweils zehnmal.

Schritt 3: Berechnen Sie die Teststatistik

Die Chi-Quadrat-Teststatistik X ² wird wie folgt berechnet:

• X ² = Σ(OE) ² / E

Die folgende Tabelle zeigt, wie diese Teststatistik berechnet wird:

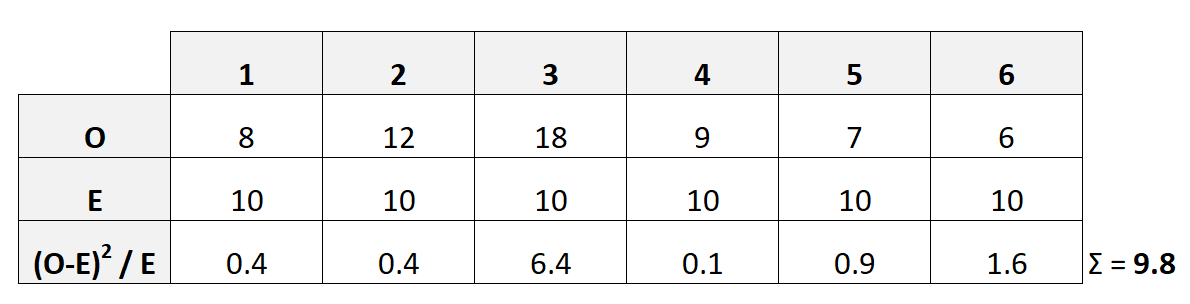
In diesem Fall beträgt X ² 9,8 .

Schritt 4: Finden Sie den kritischen Wert

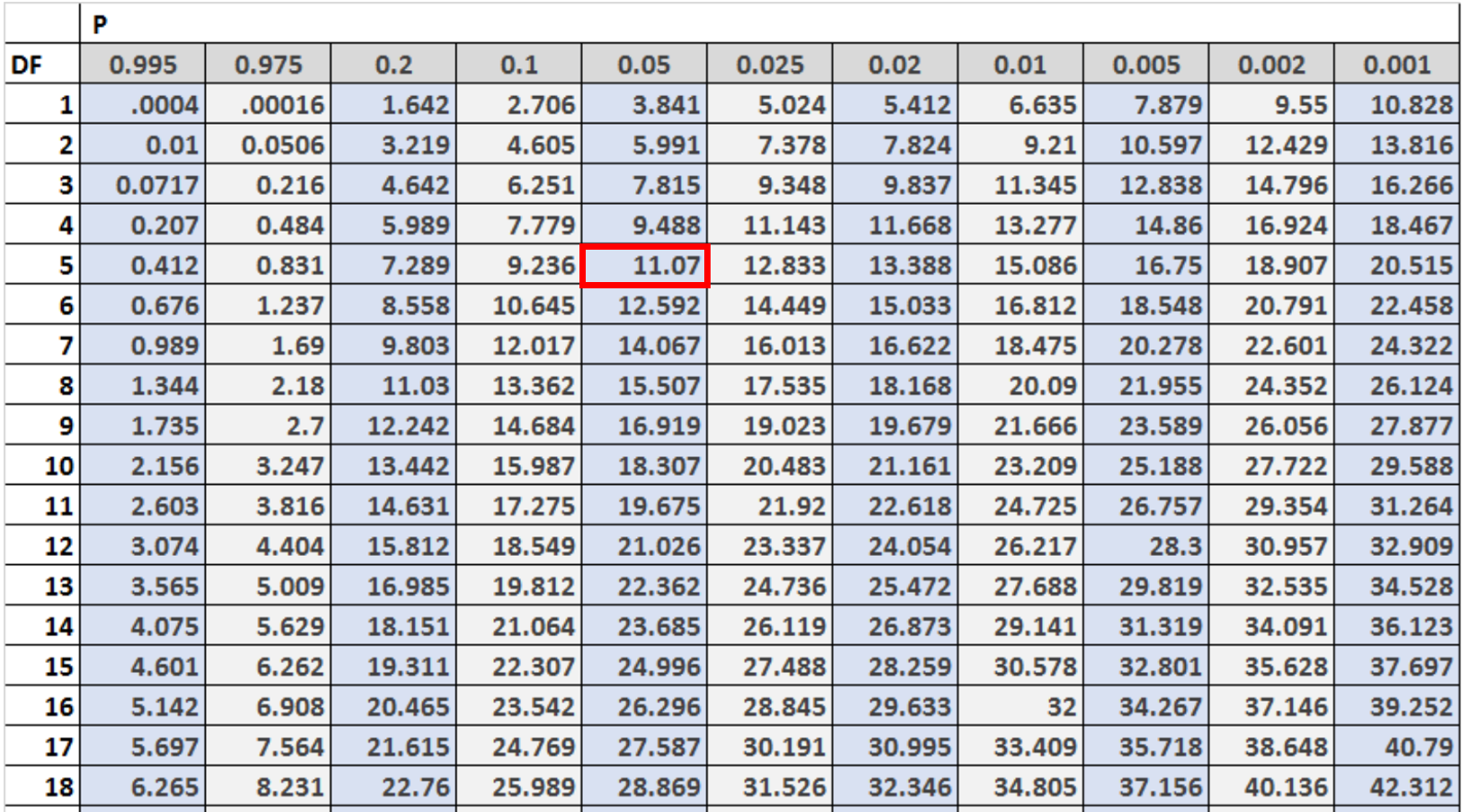
Als nächstes müssen wir den kritischen Wert in der Chi-Quadrat-Verteilungstabelle finden, der α = 0,05 und df = (#Kategorien – 1) entspricht.

In diesem Fall gibt es 6 Kategorien, also verwenden wir df = 6 – 1 = 5 .

Wir können sehen, dass der kritische Wert 11,07 beträgt.

Schritt 5: Die Nullhypothese ablehnen oder nicht ablehnen

Da unsere Teststatistik unter dem kritischen Wert liegt, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass wir nicht genügend Beweise haben, um zu sagen, dass die Würfel unfair sind.

Zusätzliche Ressourcen

Die folgenden Ressourcen bieten zusätzliche Informationen zum Chi-Quadrat-Anpassungstest:

Einführung in den Chi-Quadrat-Anpassungstest
So führen Sie einen Chi-Quadrat-Anpassungstest in R durch
Rechner für Chi-Quadrat-Anpassungstests