Harmonischer durchschnitt

Hier erklären wir, was das harmonische Mittel ist und wie es berechnet wird (Formel). Zusätzlich berechnen wir Schritt für Schritt das harmonische Mittel eines Beispiels. Sie finden auch einen Rechner, mit dem Sie das harmonische Mittel eines beliebigen Datensatzes ermitteln können. Und schließlich können Sie die Eigenschaften des harmonischen Mittelwerts erkennen.

Was ist das harmonische Mittel?

Das harmonische Mittel ist ein zentrales Positionsmaß der deskriptiven Statistik. Der harmonische Mittelwert wird berechnet, indem die Gesamtzahl der statistischen Daten durch die Summe der Kehrwerte jedes Werts dividiert wird.

Der harmonische Durchschnitt wird zur Berechnung von Durchschnittsgeschwindigkeiten und -zeiten oder zur Durchführung elektronischer Berechnungen verwendet. Diese Funktion unterscheidet den harmonischen Durchschnitt von anderen Arten von Durchschnittswerten, die häufig zur Berechnung von Durchschnittspreisen oder -prozentsätzen verwendet werden.

Die Formel für das harmonische Mittel lautet also wie folgt:

Der harmonische Durchschnitt wird normalerweise durch ein großes H dargestellt.

Andere Arten von Durchschnittswerten sind der arithmetische Durchschnitt, der gewichtete Durchschnitt, der quadratische Durchschnitt und der geometrische Durchschnitt. Der harmonische Durchschnitt hat im Vergleich zu anderen Durchschnittstypen Vor- und Nachteile. Im Folgenden werden wir sehen, welche das sind.

So berechnen Sie das harmonische Mittel

Um das harmonische Mittel zu berechnen, müssen folgende Schritte durchgeführt werden:

1. Berechnen Sie den Kehrwert aller statistischen Daten in der Stichprobe.
2. Addieren Sie alle berechneten Inversen.
3. Teilen Sie die Gesamtzahl der Daten durch die im vorherigen Schritt ermittelte Summe.
4. Das erhaltene Ergebnis ist das harmonische Mittel der statistischen Stichprobe.

👉 Wie Sie sehen, erfordert die Ermittlung des harmonischen Mittelwerts eines Datensatzes viele Operationen, sodass es ziemlich mühsam ist, dies manuell durchzuführen. Daher empfehlen wir zur Berechnung des harmonischen Mittels die Verwendung des untenstehenden Rechners.

Beispiel für ein harmonisches Mittel

Nachdem wir die Theorie über den harmonischen Mittelwert kennengelernt haben, werden wir sehen, wie man den harmonischen Mittelwert eines Datensatzes ermittelt, indem man ein schrittweises Beispiel für den Preis einer Aktie löst.

• Eine Person kauft fünf Jahre lang jedes Jahr Aktien eines Unternehmens. In diesem Zeitraum schwankte der Aktienkurs stark: Im ersten Jahr war jede Aktie 7 € wert, im zweiten Jahr 10 €, im dritten Jahr 15 €, im vierten Jahr erlitt das Unternehmen erhebliche finanzielle Verluste und die Der Preis fiel auf 6 € pro Aktie und schließlich tätigte das Unternehmen im fünften Jahr eine große Investition, die den Preis auf 11 € erhöhte. Wie hoch war der durchschnittliche Kaufpreis der Aktien?

Eine Möglichkeit wäre die Berechnung des arithmetischen Mittels, also die Addition aller Preise und die Division durch fünf. Da die Anschaffungen jedoch in unterschiedlichen Jahren getätigt wurden, wäre die Bildung des arithmetischen Durchschnitts ein Fehler. Wir müssen daher das harmonische Mittel aller Preise finden.

Als nächstes wenden wir die harmonische Mittelwertformel an:

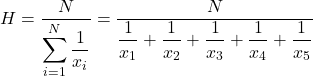
Und dann setzen wir die problematischen Preiswerte in die Formel ein und berechnen den harmonischen Mittelwert:

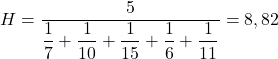
Da es sich um fünf verschiedene Informationen handelt, müssen Sie in den Zähler des Bruchs eine Fünf setzen.

Daher beträgt der durchschnittliche Preis der von Ihnen in diesem Zeitraum erworbenen Aktien 8,82 Euro je Aktie.

Harmonischer Mittelwertrechner

Mit dem folgenden Rechner können Sie das harmonische Mittel eines beliebigen statistischen Datensatzes berechnen.

Sie müssen Zahlen mit dem Punkt als Dezimaltrennzeichen eingeben und die Zahlen durch ein Leerzeichen trennen. Denken Sie daran, dass zur Ermittlung des harmonischen Mittelwerts kein Wert Null sein darf.

Eigenschaften des harmonischen Mittelwerts

Das harmonische Mittel weist folgende Eigenschaften auf:

• Große Werte haben nur geringe Auswirkungen auf den harmonischen Mittelwert eines Ensembles, d. h. ein sehr großer Wert im Verhältnis zu anderen Daten führt nicht zu einer merklichen Änderung des harmonischen Mittelwerts.

• Andererseits hat ein kleiner Wert großen Einfluss auf das harmonische Mittel eines Ensembles und verringert dessen Wert erheblich. Tatsächlich nehmen die Kehrwerte des Nenners der Formel dann sehr große Werte an.

• Das harmonische Mittel kann nicht berechnet werden, wenn einer der Daten Null ist, da dies zu Unbestimmtheit in der Formel führen würde. In einem solchen Fall wird das harmonische Mittel als undefiniert bezeichnet.

• Der Kehrwert des harmonischen Mittels entspricht dem arithmetischen Mittel der Kehrwerte der Beobachtungen.

• Für dieselbe Datengruppe ist das harmonische Mittel kleiner oder gleich dem arithmetischen Mittel.

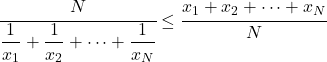
Berechnen Sie das harmonische Mittel mit Excel

Wie wir gesehen haben, kann die manuelle Berechnung des harmonischen Mittels recht mühsam sein, da viele Berechnungen durchgeführt werden müssen. Und noch komplizierter wird es, wenn Sie über große Datenmengen verfügen. Um den harmonischen Mittelwert zu ermitteln, empfehlen wir daher die Verwendung eines Taschenrechners oder des Excel-Programms.

Das harmonische Mittel in Excel wird mit der Formel MEAN.ARMO berechnet. Das heißt, um das harmonische Mittel eines Datensatzes zu berechnen, müssen Sie ihn in eine Excel-Tabelle kopieren und alle Daten in die Funktion MEAN.ARMO eingeben.

Um beispielsweise das harmonische Mittel der oben gelösten Übung zu erhalten, schreiben Sie in eine Excel-Zelle =MEDIA.ARMO(7;10;15;6;11) .

Beachten Sie, dass die Funktion einen Fehler zurückgibt, wenn einer der Werte Null ist, da das harmonische Mittel einer Reihe statistischer Werte nicht bestimmt werden kann, wenn einer dieser Werte Null ist.