Häufigkeitsverteilung

In diesem Artikel wird erklärt, was Häufigkeitsverteilungen sind und wie sie erreicht werden. Außerdem finden Sie Schritt-für-Schritt-Beispiele zu Häufigkeitsverteilungen und können zusätzlich anhand gelöster Aufgaben üben.

Was ist eine Häufigkeitsverteilung?

In der Statistik ist die Häufigkeitsverteilung eine Tabelle, in der die verschiedenen Werte einer Stichprobe in Zeilen gruppiert werden und in jeder Spalte ein Häufigkeitstyp jedes Wertes angezeigt wird. Daher wird die Häufigkeitsverteilung verwendet, um alle Arten von Häufigkeiten in einem Datensatz anzuzeigen.

Genauer gesagt umfasst eine Häufigkeitsverteilung die absolute Häufigkeit, die kumulative absolute Häufigkeit, die relative Häufigkeit und die kumulative relative Häufigkeit.

Eines der Merkmale von Häufigkeitsverteilungen besteht darin, dass sie sehr nützlich sind, um eine statistische Stichprobe einer quantitativen Variablen und einer qualitativen Variablen zusammenzufassen.

So erstellen Sie eine Häufigkeitsverteilung

Um eine Häufigkeitsverteilung durchzuführen, müssen Sie die folgenden Schritte ausführen:

1. Organisieren Sie die Daten in verschiedene Kategorien und erstellen Sie eine Tabelle, in der jede Zeile einer Kategorie entspricht.
2. Berechnen Sie die absolute Häufigkeit jeder Kategorie in der zweiten Spalte der Tabelle.
3. Berechnen Sie die kumulative absolute Häufigkeit jeder Kategorie in der dritten Spalte der Tabelle.
4. Berechnen Sie die relative Häufigkeit jeder Kategorie in der vierten Spalte der Tabelle.
5. Berechnen Sie die kumulative relative Häufigkeit jeder Kategorie in der fünften Spalte der Tabelle.
6. Optional können zwei Spalten hinzugefügt werden, in denen die relative Häufigkeit und die kumulierte relative Häufigkeit in Prozent berechnet werden. Dazu müssen Sie lediglich beide Spalten mit 100 multiplizieren.

Beispiel einer Häufigkeitsverteilung

Nachdem wir die Definition der Häufigkeitsverteilung und die Theorie zu ihrer Konstruktion kennengelernt haben, wird in diesem Abschnitt ein Beispiel Schritt für Schritt gelöst.

• Die im Fach Statistik in einer Klasse mit 30 Schülern erzielten Noten lauten wie folgt. Konstruieren Sie eine Häufigkeitsverteilung des Datensatzes.

Da alle Zahlen nur ganze Zahlen sein können, handelt es sich um eine diskrete Variable. Eine Gruppierung der Daten in Intervalle ist daher nicht erforderlich.

Um eine Häufigkeitsverteilung zu erstellen, müssen wir eine Tabelle erstellen, in der jeder unterschiedliche Wert eine Zeile darstellt, und dann müssen wir die absolute Häufigkeit jedes Werts ermitteln:

Beachten Sie, dass die Summe aller absoluten Häufigkeiten der Gesamtzahl der Daten entspricht. Wenn diese Regel nicht eingehalten wird, bedeutet das, dass Sie vergessen haben, bestimmte Informationen anzugeben.

Da wir nun die absolute Häufigkeit kennen, müssen wir die kumulative absolute Häufigkeit berechnen. Für diese Berechnung haben wir zwei Möglichkeiten: Entweder wir addieren die absolute Häufigkeit des Werts plus alle absoluten Häufigkeiten der kleinsten Werte, oder wir addieren umgekehrt die absolute Häufigkeit des Werts plus die kumulative absolute Häufigkeit des vorherigen Werts.

Die kumulative absolute Häufigkeit des letzten Wertes entspricht immer der Gesamtzahl der Daten. Mit diesem Trick können Sie überprüfen, ob die Berechnungen korrekt sind.

Als nächstes müssen wir die relative Häufigkeit bestimmen, die berechnet wird, indem die absolute Häufigkeit durch die Gesamtzahl der Datenpunkte (30) dividiert wird:

Beachten Sie, dass die Summe aller relativen Häufigkeiten immer gleich 1 ist, andernfalls bedeutet dies, dass eine bestimmte Berechnung der Häufigkeitsverteilung falsch ist.

Zum Schluss müssen wir nur noch die kumulative relative Häufigkeit extrahieren. Dazu müssen Sie die relative Häufigkeit des betreffenden Wertes plus alle vorherigen relativen Häufigkeiten oder, was auf dasselbe hinausläuft, die bisherige kumulierte relative Häufigkeit addieren:

Kurz gesagt ist die Häufigkeitsverteilung mit allen Häufigkeiten der Problemdaten wie folgt:

Häufigkeitsverteilung für gruppierte Daten

Um eine Häufigkeitsverteilung für in Intervallen gruppierte Daten zu erstellen, besteht der einzige Unterschied darin, dass der Datensatz zunächst in verschiedene Intervalle gruppiert werden muss, die übrigen Berechnungen erfolgen jedoch auf die gleiche Weise wie bei einer Häufigkeitsverteilung ohne Gruppierung der Daten.

Als Beispiel wird im Folgenden ein Problem der Erstellung einer Häufigkeitsverteilung für gruppierte Daten gelöst.

• Die Körpergröße von 20 Personen wurde gemessen und die unten aufgeführten Ergebnisse erzielt. Erstellen Sie eine Häufigkeitsverteilung, indem Sie die Daten in Intervalle unterteilen.

Die Daten in diesem Beispiel folgen einer kontinuierlichen Verteilung, da die Zahlen dezimal sein können und daher jeden beliebigen Wert annehmen können. Daher erstellen wir eine Häufigkeitsverteilung, indem wir die Daten in Intervalle gruppieren.

Obwohl es mehrere mathematische Regeln zum Erstellen der Intervalle einer Stichprobe gibt, erstellen wir in diesem Fall einfach Intervalle mit einer Breite von 10 Zehnteln.

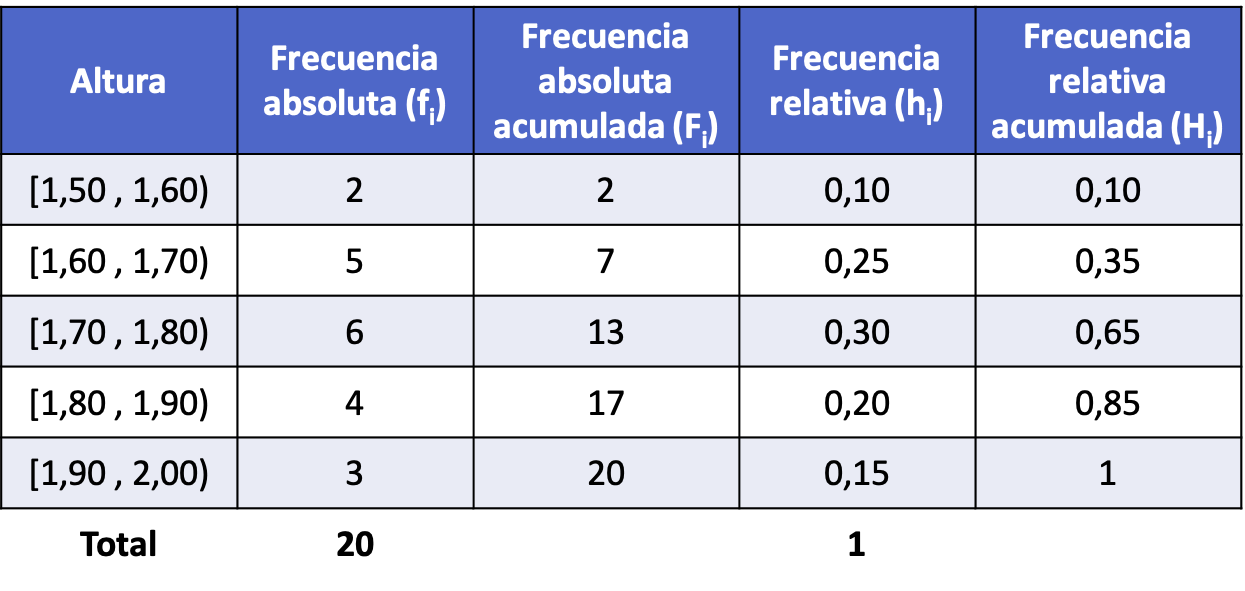
Nach der Berechnung aller Häufigkeitstypen für jedes Intervall (das Verfahren ist das gleiche wie im obigen Beispiel) sieht die Häufigkeitsverteilung mit den in Intervallen gruppierten Daten wie folgt aus:

Aufgaben zur Häufigkeitsverteilung gelöst

Übung 1

Wir haben 20 Menschen gefragt, wie oft sie im Monat ins Kino gehen und hier sind die Ergebnisse:

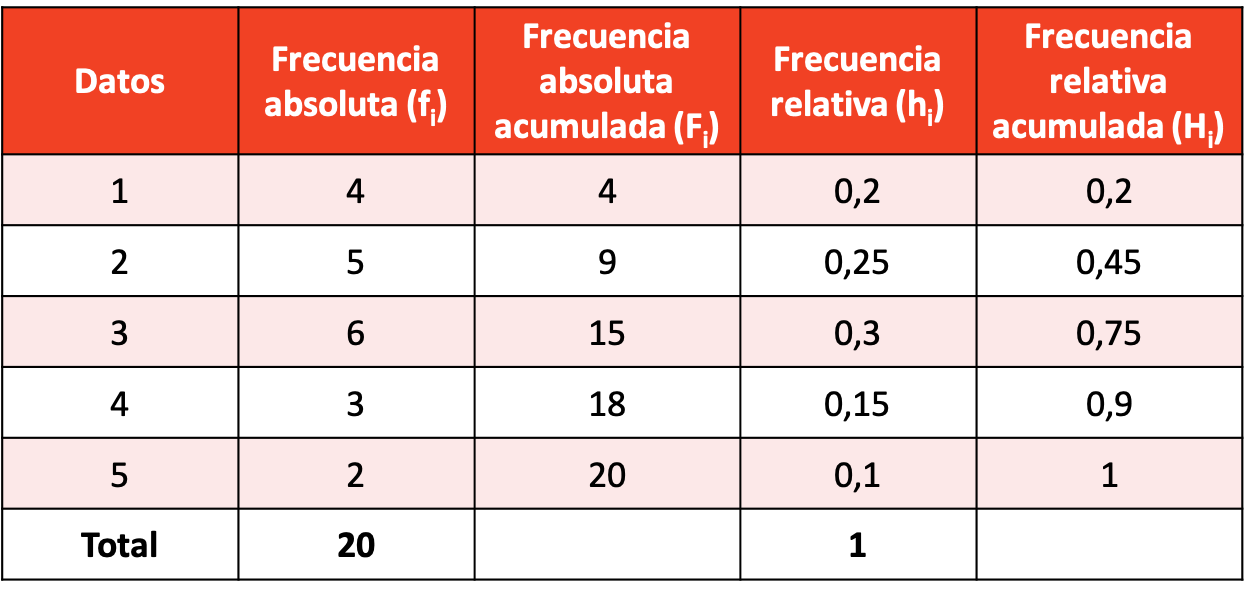
Erstellen Sie eine Häufigkeitsverteilung mit der resultierenden Datenstichprobe.

Die Häufigkeitsverteilung mit Berechnungen aller Häufigkeitsarten ist wie folgt:

Übung 2

Sie möchten eine statistische Untersuchung zum Gewicht der Arbeitnehmer in einem Unternehmen mit 36 Mitarbeitern durchführen. Hier sind die Gewichte der Arbeiter in Kilogramm:

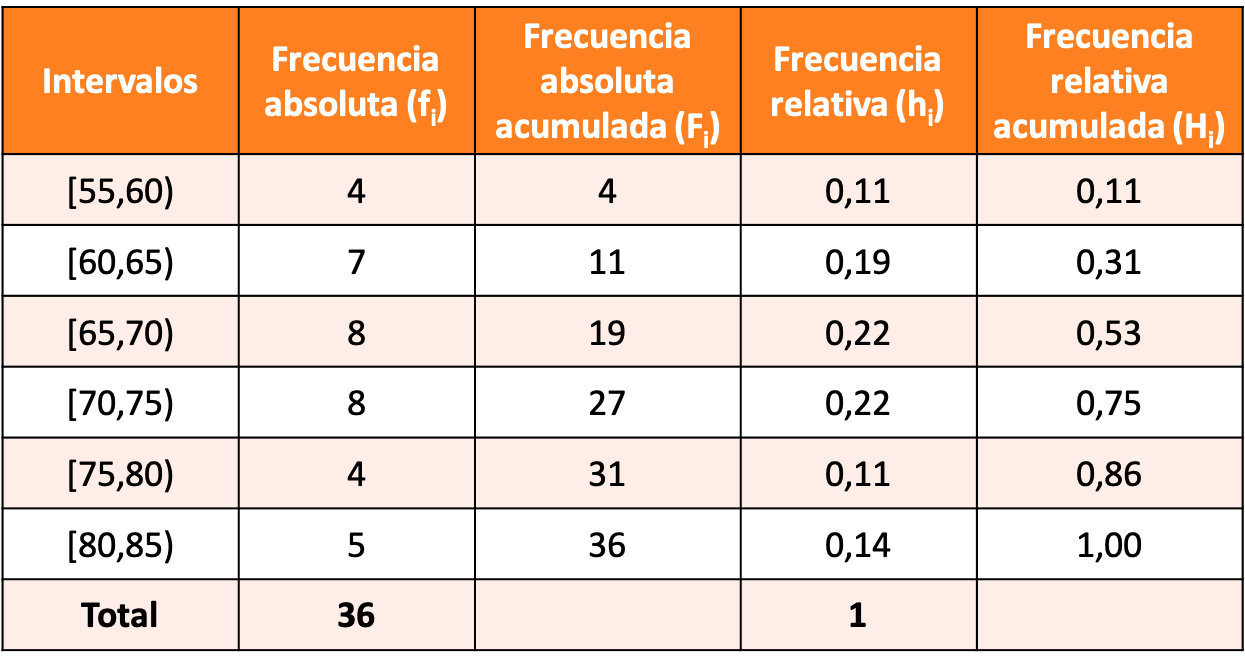
Konstruieren Sie eine Häufigkeitsverteilung mit gruppierten Daten, indem Sie Intervalle von 5 Einheiten erstellen und das erste Intervall [55,60] sein lassen.

Die Lösung der Aufgabe ist die folgende Häufigkeitsverteilung: