So berechnen sie hebelstatistiken in r

In der Statistik gilt eine Beobachtung als Ausreißer , wenn ihr Wert für die Antwortvariable viel größer ist als der Rest der Beobachtungen im Datensatz.

Ebenso gilt eine Beobachtung als hohe Hebelwirkung , wenn sie einen oder mehrere Werte für die Prädiktorvariablen aufweist, die im Vergleich zu den übrigen Beobachtungen im Datensatz viel extremer sind.

Einer der ersten Schritte bei jeder Art von Analyse besteht darin, Beobachtungen mit hohem Einfluss genauer zu betrachten, da sie einen großen Einfluss auf die Ergebnisse eines bestimmten Modells haben können.

Dieses Tutorial zeigt ein schrittweises Beispiel für die Berechnung und Visualisierung der Hebelwirkung für jede Beobachtung in einem Modell in R.

Schritt 1: Erstellen Sie ein Regressionsmodell

Zuerst erstellen wir ein multiples lineares Regressionsmodell unter Verwendung des in R integrierten mtcars- Datensatzes:

 #load the dataset
data(mtcars)

#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Schritt 2: Berechnen Sie die Hebelwirkung für jede Beobachtung

Als Nächstes verwenden wir die Funktion hatvalues() , um die Hebelwirkung für jede Beobachtung im Modell zu berechnen:

 #calculate leverage for each observation in the model
hats <- as . data . frame (hatvalues(model))

#display leverage stats for each observation
hats

                    hatvalues(model)
Mazda RX4 0.04235795
Mazda RX4 Wag 0.04235795
Datsun 710 0.06287776
Hornet 4 Drive 0.07614472
Hornet Sportabout 0.08097817
Valiant 0.05945972
Duster 360 0.09828955
Merc 240D 0.08816960
Merc 230 0.05102253
Merc 280 0.03990060
Merc 280C 0.03990060
Merc 450SE 0.03890159
Merc 450SL 0.03890159
Merc 450SLC 0.03890159
Cadillac Fleetwood 0.19443875
Lincoln Continental 0.16042361
Chrysler Imperial 0.12447530
Fiat 128 0.08346304
Honda Civic 0.09493784
Toyota Corolla 0.08732818
Toyota Corona 0.05697867
Dodge Challenger 0.06954069
AMC Javelin 0.05767659
Camaro Z28 0.10011654
Pontiac Firebird 0.12979822
Fiat X1-9 0.08334018
Porsche 914-2 0.05785170
Lotus Europa 0.08193899
Ford Pantera L 0.13831817
Ferrari Dino 0.12608583
Maserati Bora 0.49663919
Volvo 142E 0.05848459

Typischerweise schauen wir uns Beobachtungen mit einem Hebelwert von mehr als 2 genauer an.

Eine einfache Möglichkeit hierfür besteht darin, die Beobachtungen nach ihrem Hebelwert in absteigender Reihenfolge zu sortieren:

 #sort observations by leverage, descending
hats[ order (-hats[' hatvalues(model) ']), ]

 [1] 0.49663919 0.19443875 0.16042361 0.13831817 0.12979822 0.12608583
 [7] 0.12447530 0.10011654 0.09828955 0.09493784 0.08816960 0.08732818
[13] 0.08346304 0.08334018 0.08193899 0.08097817 0.07614472 0.06954069
[19] 0.06287776 0.05945972 0.05848459 0.05785170 0.05767659 0.05697867
[25] 0.05102253 0.04235795 0.04235795 0.03990060 0.03990060 0.03890159
[31] 0.03890159 0.03890159

Wir können sehen, dass der höchste Hebelwert 0,4966 beträgt. Da diese Zahl nicht größer als 2 ist, wissen wir, dass keine der Beobachtungen in unserem Datensatz einen hohen Einfluss hat.

Schritt 3: Visualisieren Sie die Hebelwirkung für jede Beobachtung

Schließlich können wir ein schnelles Diagramm erstellen, um die Hebelwirkung für jede Beobachtung zu visualisieren:

 #plot leverage values for each observation
plot(hatvalues(model), type = ' h ')

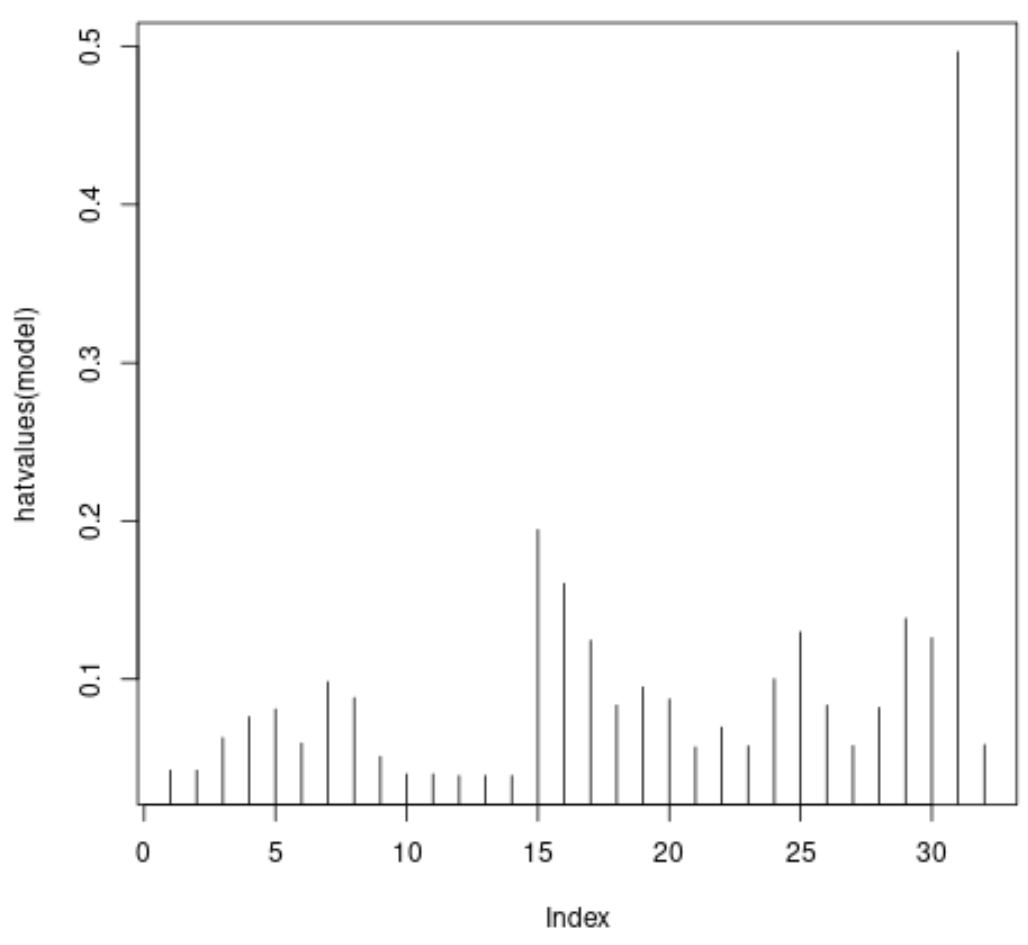
Die x-Achse zeigt den Index jeder Beobachtung im Datensatz und der y-Wert zeigt die entsprechende Leverage-Statistik für jede Beobachtung an.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So erstellen Sie ein Residuendiagramm in R