Der breusch-pagan-test: definition und beispiel

Eine der wichtigsten Annahmen der linearen Regression besteht darin, dass die Residuen auf jeder Ebene der Prädiktorvariablen mit gleicher Varianz verteilt sind. Diese Annahme wird als Homoskedastizität bezeichnet.

Wenn diese Annahme nicht berücksichtigt wird, spricht man von Heteroskedastizität in den Residuen. Wenn dies geschieht, werden die Regressionsergebnisse unzuverlässig.

Eine Möglichkeit, visuell zu erkennen, ob Heteroskedastizität vorliegt, besteht darin, ein Diagramm der Residuen gegenüber den angepassten Werten aus dem Regressionsmodell zu erstellen.

Wenn sich die Residuen bei höheren Werten im Diagramm stärker ausbreiten, ist dies ein verräterisches Zeichen für das Vorhandensein von Heteroskedastizität.

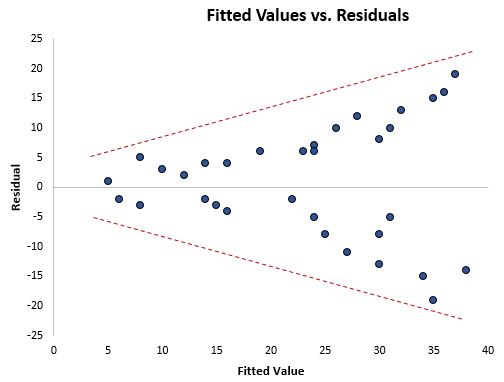
Ein formaler statistischer Test, mit dem wir feststellen können, ob Heteroskedastizität vorliegt, ist der Breusch-Pagan-Test .

Dieses Tutorial bietet eine kurze Erläuterung des Breusch-Pagan-Tests zusammen mit einem Beispiel.

Was ist der Breusch-Pagan-Test?

Der Breusch-Pagan-Test wird verwendet, um zu bestimmen, ob in einem Regressionsmodell Heteroskedastizität vorliegt oder nicht.

Der Test verwendet die folgenden Null- und Alternativhypothesen :

• Nullhypothese (H ₀ ): Homoskedastizität liegt vor (Residuen sind mit gleicher Varianz verteilt)
• Alternativhypothese ( _HA ): Heteroskedastizität liegt vor (Residuen sind nicht mit gleicher Varianz verteilt)

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (d. h. α = 0,05), lehnen wir die Nullhypothese ab und kommen zu dem Schluss, dass im Regressionsmodell Heteroskedastizität vorliegt.

Wir verwenden die folgenden Schritte, um einen Breusch-Pagan-Test durchzuführen:

1. Passen Sie das Regressionsmodell an.

2. Berechnen Sie die Quadrate der Modellresiduen.

3. Passen Sie ein neues Regressionsmodell an und verwenden Sie dabei die Quadrate der Residuen als Antwortwerte.

4. Berechnen Sie die Chi-Quadrat-X ² -Teststatistik in der Form n*R ² _neu , wobei:

• n: Die Gesamtzahl der Beobachtungen
• R ² _neu : Das R-Quadrat des neuen Regressionsmodells, das die Quadrate der Residuen als Antwortwerte verwendet

Wenn der p-Wert, der dieser Chi-Quadrat-Teststatistik mit p (der Anzahl der Prädiktoren) Freiheitsgraden entspricht, unter einem bestimmten Signifikanzniveau liegt (d. h. α = 0,05), lehnen Sie die Nullhypothese ab und schlussfolgern Sie, dass Heteroskedastizität vorliegt .

Andernfalls lehnen Sie die Nullhypothese nicht ab. In diesem Fall wird davon ausgegangen, dass Homoskedastizität vorliegt.

Beachten Sie, dass der Breusch-Pagan-Test mit den meisten Statistikprogrammen problemlos durchgeführt werden kann, sodass Sie diese Schritte wahrscheinlich nie manuell ausführen müssen. Es ist jedoch hilfreich zu wissen, was sich hinter den Kulissen abspielt.

Ein Beispiel für den Breusch-Pagan-Test

Angenommen, wir haben den folgenden Datensatz mit Informationen zu 10 verschiedenen Basketballspielern:

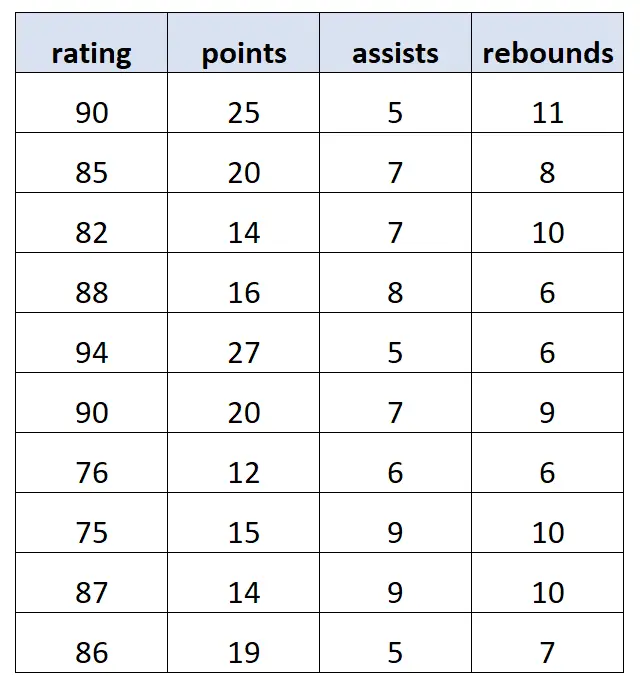
Mit statistischer Software passen wir das folgende multiple lineare Regressionsmodell an:

Punktestand = 62,47 + 1,12*(Punkte) + 0,88*(Assists) – 0,43*(Rebounds)

Anschließend verwenden wir dieses Modell, um Vorhersagen über die Bewertung jedes Spielers zu treffen und die quadrierten Residuen zu berechnen (d. h. die quadrierte Differenz zwischen der vorhergesagten Bewertung und der tatsächlichen Bewertung):

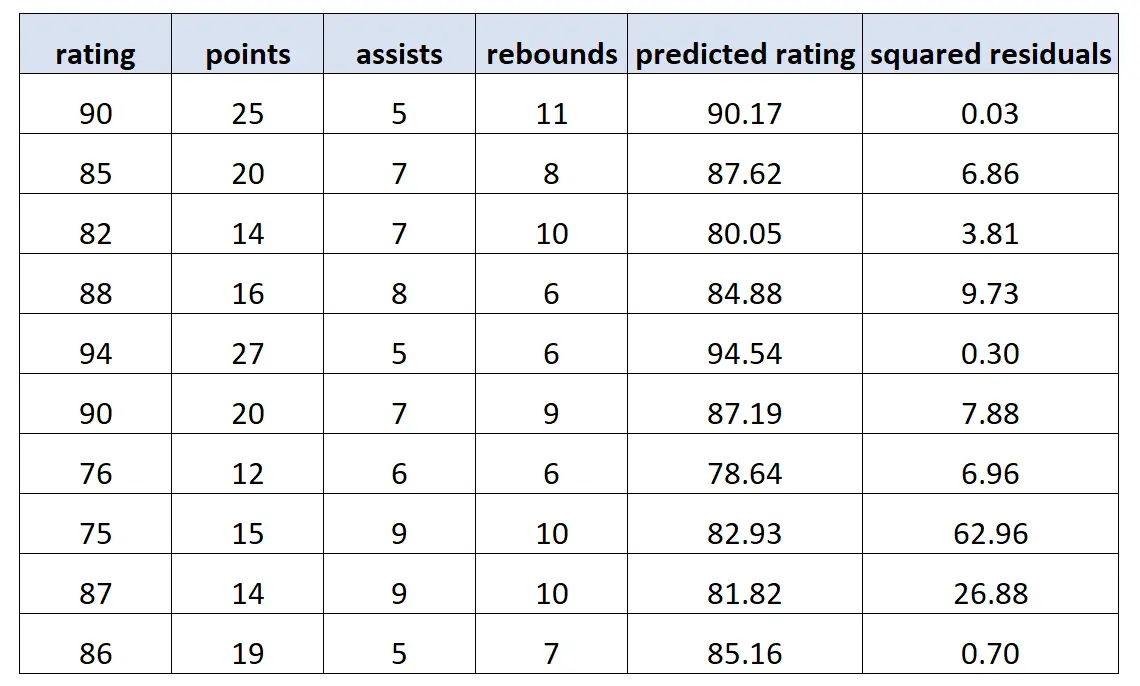
Als nächstes passen wir ein neues Regressionsmodell an, wobei wir die Quadrate der Residuen als Antwortwerte und die ursprünglichen Prädiktorvariablen erneut als Prädiktorvariablen verwenden. Wir finden Folgendes:

• n: 10
• R ² _neu : 0,600395

Unsere Chi-Quadrat-Teststatistik für den Breusch-Pagan-Test lautet also n*R ² _new = 10*.600395 = 6.00395 . Die Freiheitsgrade sind p = 3 Prädiktorvariablen.

Laut dem Chi-Quadrat-zu-P-Wert-Rechner beträgt der p-Wert, der X ² = 6,00395 mit 3 Freiheitsgraden entspricht, 0,111418 .

Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir gehen daher davon aus, dass Homoskedastizität vorliegt.

Der Breusch-Pagan-Test in der Praxis

Die folgenden Tutorials bieten Schritt-für-Schritt-Beispiele zur Durchführung des Breusch-Pagan-Tests in verschiedenen Statistikprogrammen:

So führen Sie einen Breusch-Pagan-Test in Excel durch
So führen Sie einen Breusch-Pagan-Test in R durch
So führen Sie einen Breusch-Pagan-Test in Python durch
So führen Sie einen Breusch-Pagan-Test in Stata durch